1) Постоянная (собственный вес арки) и снеговая, равномерно распределенная нагрузка по всему пролету

2) Постоянная (собственный вес арки) и снеговая, равномерно распределенная нагрузка на половине пролета
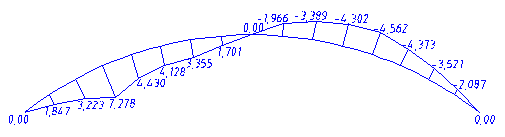
3) Постоянная (собственный вес арки) и снеговая, распределенная по треугольнику, на половине пролета
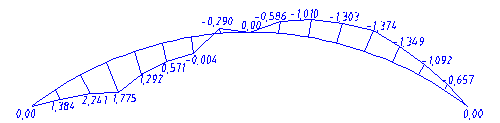
Согласно результатам таблицы расчетным сечением на прочность по деформированной схеме и устойчивость плоской формы деформирования является сечение с максимальным моментом. В нашем случае это сечения, отстающие от опор на расстояние 2,0 м.
Расчетный момент на расстоянии Х1=2,0 м равен М=-4,562 кНм.
Расчетный момент на расстоянии Х2=6,0 м равен М=-4,562 кНм.
При действии на арку собственного веса и снеговой нагрузки по прямоугольнику на правой половине пролета вертикальные опоры реакции:
VA=gр l/2+S1 l/8=1,898*8,0/2+4,496*8,0/8=7,592+4,496=12,088 кН,
VB=gр l/2+3S1 l/8=1,898*8,0/2+3*4,496*8,0/8=7,592+13,488=21,080 кН,
Распор:
Н=gрl2/(8*f)+S1l2/(16f)=1,898*8,02/(8*0,5)+4,496*8,02/(16*0,5)=30,368+35,968=
=66,336 кН,
Поперечная сила на расстоянии Х1=2,0 м от левой опоры:
Qб=VВ-q(l-X1)-S1l/2,
Qб=21,080-1,898(8,0-2,0)-4,496*8,0/2=-8,292 кН,
Продольная сила в сечении арки Х1=2,0 м от левой опоры:
Nx=2,0= Qб*sinφ+H*cosφ=-8,292*0,123+66,336*0,993=64,852 кН,
sinφ=(l/2-X1)/r=(8,0/2-2,0)/16,25=0,123,
φ=7°,
cosφ=0,993.
При действии на арку собственного веса и снеговой нагрузки по прямоугольнику на левой половине пролета вертикальные опорные реакции:
VA=gр l/2+S1 l/8=1,898*8,0/2+4,496*8,0/8=7,592+4,496=12,088 кН,
VB=gр l/2+3S1 l/8=1,898*8,0/2+3*4,496*8,0/8=7,592+13,488=21,080 кН,
Распор:
Н=gрl2/(8*f)+S1l2/(16f)=1,898*8,02/(8*0,5)+4,496*8,02/(16*0,5)=
=30,368+35,968=66,336 кН,
Поперечная сила на расстоянии Х2=6,0 м от левой опоры:
Qб=VA-qX2-S1l/2,
Qб=12,088-1,898*6,0-4,496*8,0/2=-17,284 кН,
Продольная сила в сечении арки Х2=14,5 м от левой опоры:
Nx=6,0= Qб*sinφ+H*cosφ=-17,284*(-0,123)+66,336*0,993=67,998 кН,
sinφ=(l/2-X2)/r=(8,0/2-6,0)/16,25=-0,123,
φ=-7°,
cosφ=0,993.
2.2.2.3. Конструктивный расчет арки.
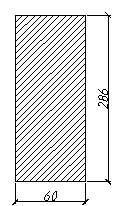
Принимаем сечение ребра купола (арки) 11 досок толщиной 26 мм (после острожки и усушки досок толщиной 32 мм): h=26*11=286 мм. Доски принимаем шириной 75 мм. Длина полуарки меньше 12 м, поэтому на острожку по боковым граням арки идет 15 мм: b=75-15=60 мм.
Поперечное сечение арки:
1. Расчет арки на прочность:
σ=N/Fрасч+Мд/Wрасч≤ Rc,
N=67,998 кН,
Fрасч=b*h=0,060*0,286=0,0172 м2- площадь расчетного сечения арки,
Wрасч=b*h2/6=0,060*0,2862/6=0,000818 м2- расчетный момент сопротивления попе-речного сечения,
Мд=М/ξ- изгибающий момент от действия поперечных и продольных нагрузок,
М=-4,562 кНм,
ξ=1-λ²*N0/(3000*Rc*Fбр)- коэффициент, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента. Согласно СНиП при определении ξ сжимающую силу следует принимать в ключевом шарнире N0=Н=66,336 кН.
λ=l0/r=0,58S/√h²/12=0,58*8,08/√0,286²/12=56,736 м- гибкость арки,
ξ=1-56,736²*66,336*10-3/(3000*14*0,0172)=0,704
3000-коэффициент древесины,
Мд=4,562/0,704=6,480 кНм,
σ=67,998/0,0172+6,480/0,000818=11875 кН/ м2 ≤ 14*1*1,05*1,
σ=11,875 МПа≤ 14,7 МПа.
Условие прочности выполняется.
2. Расчет трехшарнирной арки на устойчивость плоской формы деформирования:
N/(φRcFбр)+(Мд/(φМRиWбр))п≤ 1,
Принимаем раскрепление сжатой грани арки панелями через 1,5 м.
п=2- для элементов без закрепления растянутой зоны из плоскости деформирования,
lp=1,5 м- расчетная длина,
![]()
![]() ry=√b²/12=√0,060²/12=0,0173 м- радиус инерции сечения арки
относительно оси У,
ry=√b²/12=√0,060²/12=0,0173 м- радиус инерции сечения арки
относительно оси У,
λ=lp/ry=1,5/0,0173=89,705- гибкость арки,
φ=3000/λ²=3000/(86,7052)=0,399- коэффициент продольного изгиба ,
3000-коэффициент для древесины,
φМ=140Kфb2/(lp*h)- коэффициент для изгибаемых элементов прямоугольного сечения,
Kф=1,13-0,13α- коэффициент, определенный из условия закрепления элемента только по концам участка lp при параболической форме эпюры,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.