ОАО «РЖД»
Сибирский Государственный Университет Путей Сообщения
Кафедра «Строительные конструкции и здания на железнодорожном транспорте»
Расчётная работа
Реконструкция и определение сил
сейсмического воздействия на ферму
Выполнил: ст. гр. П -511
Веймер О.А.
Проверил: Казарновский В.С.
2007
Исходные данные
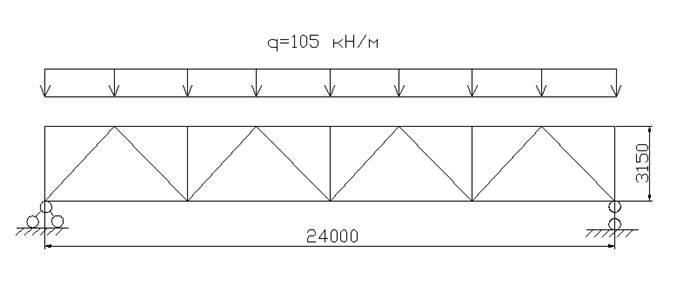
Рисунок 1 - Расчетная схема фермы
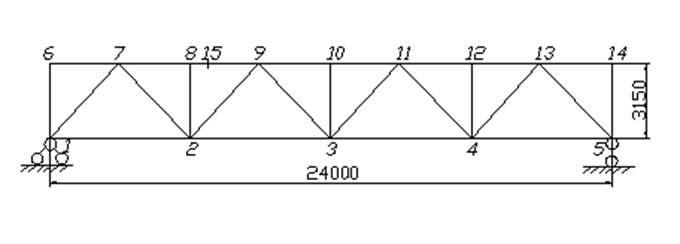
Рисунок 2 - Номера узлов, стержней
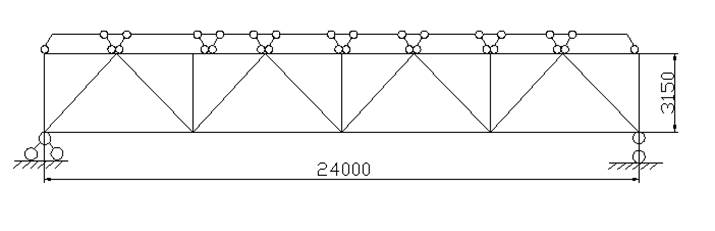
Рисунок 3 - Расчетная схема фермы с учетом работы плит покрытия
Сечения стержней фермы
·
Верхний
пояс ![]() 200 х 14, А=109,2
см2
200 х 14, А=109,2
см2
Jх=4192 см4
·
Нижний
пояс ![]() 180 х 12, А=84,38 см2
180 х 12, А=84,38 см2
Jх=2632,371 см4
·
Опорные
раскосы ![]() 125 х 12, А=57,78
см2
125 х 12, А=57,78
см2
Jх=843,592 см4
·
Раскосы
![]() 125 х 10, А=48,66 см2
125 х 10, А=48,66 см2
Jх=719,128 см4
·
Стойки
![]() 100 х 10,
А=38,48 см2
100 х 10,
А=38,48 см2
Jх=357,635 см4
Необходимо провести статический расчет на:
1. Полную нагрузку Fп=105х3=415кН, приложенную в узлах фермы.
2. Полную нагрузку Fп=415кН, приложенную в узлах фермы (сила с 8 узла перемещается в смещённый узел 15).
3. Единичную силу F= 1кН, приложенную по всем узлам поочерёдно.
4. Внеузловое приложение нагрузки Fп (с 8 узла смещена в узел 15), с учетом работы плит покрытия.
Расчет произведен в программе INTAB. Результаты расчета приведены в приложении 1.
I РЕКОНСТРУКЦИЯ
Определение несущей способности верхнего пояса
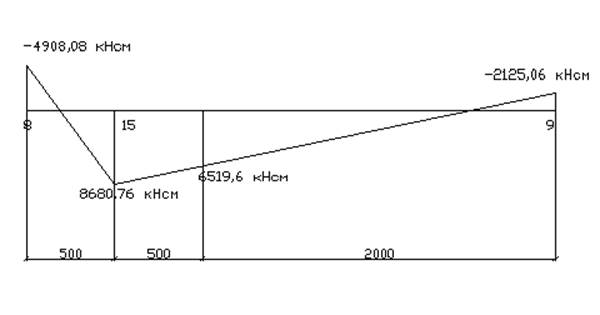
Рисунок 4- Эпюра М
Верхний
пояс состоит из ![]() 200 х 14,
А=109,2 см2
200 х 14,
А=109,2 см2
Jх=4192 см4
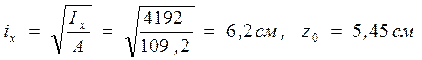
Условие прочности:
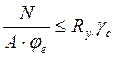
Коэффициент je определяю в зависимости
от условной гибкости ![]() и приведенного относительного
эксцентриситета mef, определяемого по формуле
и приведенного относительного
эксцентриситета mef, определяемого по формуле
mef = h mх,
где h - коэффициент влияния формы сечения, определяемый по табл. 73 СНиП;
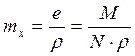 - относительный эксцентриситет,
- относительный эксцентриситет, 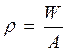 .
.
М![]() = 6519,6 кН·см, N=1801,988 кН.
= 6519,6 кН·см, N=1801,988 кН.
С 255: R![]() =240 МПа ,Е=2,06·10
=240 МПа ,Е=2,06·10![]() МПа ,γ
МПа ,γ![]() =0,95
=0,95
![]()
mх=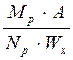 =
=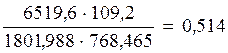
η =1,8+0,12·0,514=1,86
mef = h mх= 1,86·0,514=0,96
![]() =
=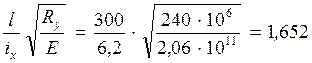
По
СНиП определяю φ![]() =0,585
=0,585
Проверка:
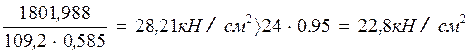
Сечение не удовлетворяет условию прочности.
Проверка несущей способности при совместной работе фермы с
железобетонными плитами покрытия
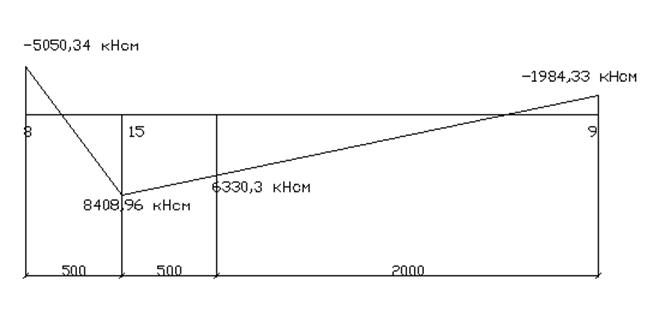
Рисунок 5 - Эпюра М
Определяем несущую способность:
М![]() = 6330,3 кН·см, N=1205,857 кН.
= 6330,3 кН·см, N=1205,857 кН.
С
255: R![]() =240 МПа ,Е=2,06·10
=240 МПа ,Е=2,06·10![]() МПа ,γ
МПа ,γ![]() =0,95
=0,95
![]()
mх=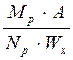 =
=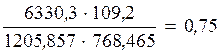
η =1,8+0,12·0,75=1,89
mef = h mх= 1,89·0,75=1,42
![]() =
=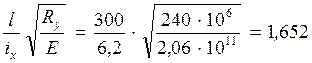
По
табл. 74 СНиП II-23-81 определяю φ![]() =0,505
=0,505
Проверка:
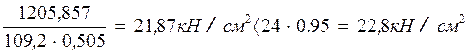
Прочность верхнего пояса обеспечена.
Определение несущей способности опорного раскоса
а) б) в)
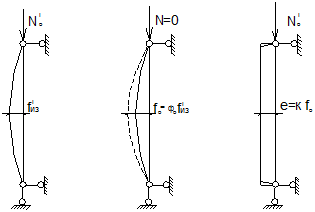
Рисунок 6-Определение эквивалентного эксцентриситета
а- состояние измерения; б- ненагруженное состояние; в- схема с эксцентриситетом
Опорный
раскос состоит из ![]() 125
х 12, А=57,78 см2
125
х 12, А=57,78 см2
Jх=843,592 см4
ix=3,82 см
z0=3,5275см
Определим несущую способность при полной гибкости:
[N]=φ·A·R![]() ·
·![]()
![]()
λ
=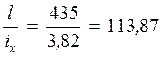
По СНиП определяем φ= 0,46
[N]=0,46·57,78·10![]() ·240·10
·240·10![]() ·0,9
= 574,1 кН.
·0,9
= 574,1 кН.
Определим несущую способность при относительной гибкости
а) выгиб вниз
[N]=φ![]() ·A·R
·A·R![]() ·
·![]()
Принимаю
f![]() =10 мм.
=10 мм.
Определяю
коэффициент К перехода от максимальной стрелки искривления к эквивалентному
эксцентриситету, принимая ![]() где
где ![]()
Момент
сопротивления определяю относительно верхней грани 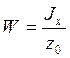 ;
;
m![]() =
=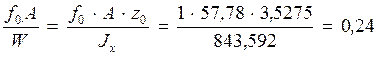
![]() =
=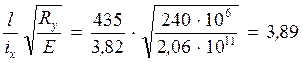
Коэффициент
влияния формы сечения η=1,8+0,12·![]()
η=1,8+0,12·0,24=1,83.
К
=0,82+(0,1 ![]() )/
)/ ![]() =
=![]() .
.
![]()
Определяю
φ![]() в зависимости от
в зависимости от ![]() =3,89 и
=3,89 и ![]()
φ![]() =0,434
=0,434
[N]=0,434·57,78·10-4·240·10![]() ·0,9=541,7
кН.
·0,9=541,7
кН.
Используя изложенный выше алгоритм, определяю несущую способность при выгибе
вниз для f![]() =20, 30, 40 и
50мм. Результаты расчёта представляю в виде графика.
=20, 30, 40 и
50мм. Результаты расчёта представляю в виде графика.
f![]() =20мм [N] =458 кН
=20мм [N] =458 кН
f![]() =30мм [N] =406,9 кН
=30мм [N] =406,9 кН
f![]() =40мм [N] =363,2 кН
=40мм [N] =363,2 кН
f![]() =50мм [N] =328,2 кН
=50мм [N] =328,2 кН
б) выгиб вверх
Принимаю
f![]() =10 мм. Момент сопротивления определяю
относительно нижней грани:
=10 мм. Момент сопротивления определяю
относительно нижней грани:
W=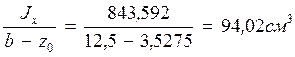
m![]() =
=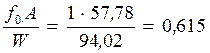 .
.
Коэффициент влияния формы сечения:
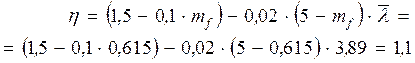
К=![]()
![]()
Определяю φ![]() в зависимости от
в зависимости от ![]() =3,89 и
=3,89 и ![]()
φ![]() =0,396.
=0,396.
[N]=0,396·57,78·10-4·240·10![]() ·0,9=494,2 кН
·0,9=494,2 кН
Используя
изложенный выше алгоритм, определяю несущую способность при выгибе вверх для f![]() =20, 30, 40 и 50мм. Результаты расчёта
представляю на графике.
=20, 30, 40 и 50мм. Результаты расчёта
представляю на графике.
f![]() =20мм [N] =409,4 кН
=20мм [N] =409,4 кН
f![]() =30мм [N] =350,7 кН
=30мм [N] =350,7 кН
f![]() =40мм [N] =312 кН
=40мм [N] =312 кН
f![]() =50мм [N] =282,1 кН
=50мм [N] =282,1 кН
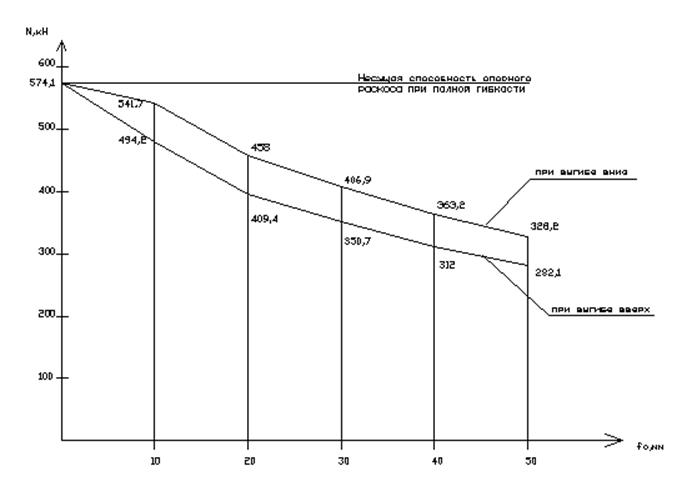
Рисунок 7 – Зависимость между несущей способностью и эксцентриситетом приложения силы
II СЕЙСМИКА
Определение сил сейсмического воздействия
В общем случае сила сейсмического воздействия в точке «к» по i-ой главной форме собственных колебаний определяется следующем выражением:
![]() ,
,
где ![]() -коэффициенты,
зависящие от конструктивного решения.
-коэффициенты,
зависящие от конструктивного решения.
А – коэффициент сейсмичности. При сейсмичности 8 баллов А = 0,2.
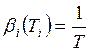 -динамический коэффициент. В пределах
-динамический коэффициент. В пределах 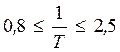
![]() , где
, где ![]() -
прогиб фермы в середине пролёта от расчётной нагрузки, соответствующей особому
сочетанию.
-
прогиб фермы в середине пролёта от расчётной нагрузки, соответствующей особому
сочетанию.
![]() -коэффициент разложения величины полной
сейсмической нагрузки в ряд по формам собственных колебаний, зависит от формы
деформации сооружения при его собственных колебаниях по i-ой форме и от
места приложения нагрузки
-коэффициент разложения величины полной
сейсмической нагрузки в ряд по формам собственных колебаний, зависит от формы
деформации сооружения при его собственных колебаниях по i-ой форме и от
места приложения нагрузки ![]() . Значение
. Значение ![]() определяется по формуле
определяется по формуле
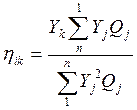 ,
,
где ![]() -
смещение сооружения при собственных колебаниях в рассматриваемой точке к, где в
соответствии с расчетной схемой принята сосредоточенная масса.
-
смещение сооружения при собственных колебаниях в рассматриваемой точке к, где в
соответствии с расчетной схемой принята сосредоточенная масса.
Для системы с 1-ой степенью свободы сила сейсмического воздействия:
![]()
![]()
![]() ,
, ![]() .
.
Определение характеристик собственных колебаний
Приближенный метод
Максимальное перемещение от загружения 1
в середине пролёта (узел 10) ![]()
Принимаю закон перемещения масс по параболе
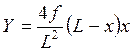 ,
,
где L-пролёт фермы, м.
х- расстояние до рассматриваемой массы, м.
Для упрощения расчётов принимаю f =1 - в середине пролёта.
![]() ,
,![]() ,
,![]() ,
, ![]()
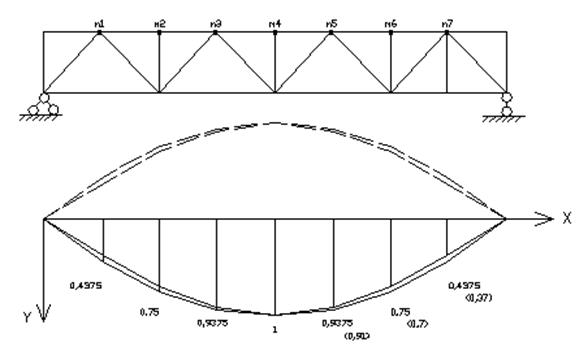
Рисунок 8 –Перемещения точек верхнего пояса.
Точный метод
Метод степенной итерации
Составляем матрицу податливости ![]() =А и умножаем её на единичный вектор
=А и умножаем её на единичный вектор ![]() .
.
![]() ,
, 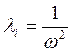
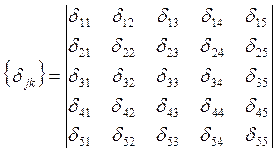 ,
,
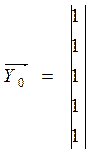
где
![]() - перемещения узлов верхнего пояса.
- перемещения узлов верхнего пояса.
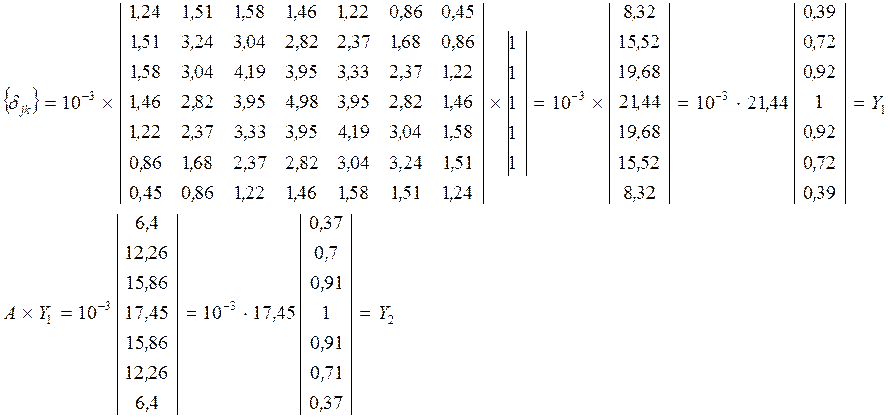
![]()
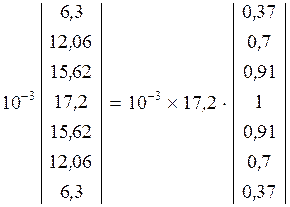
![]() ,
, ![]()
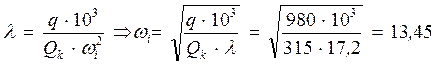
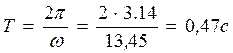 .
.
Сравнивая результаты, полученные приближенным и упрощённым точным способами, делаю вывод, что периоды практически равные. При расчете фермы в ПК SCADзначение периода оказалось равным Т = 0,683525с.
Определим силу сейсмического воздействия:
А
= 0,2; ![]() ;
; ![]()
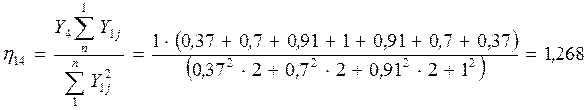
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.