Моделирование работы регулировочного участка цеха, страница 2

По временной диаграмме с учётом всех возникающих условий строится блок-схема, изображённая на рисунке 3.

При построении алгоритма использовались следующие переменные:

B –  количество агрегатов на первичной регулировке;

С –  количество агрегатов на вторичной регулировке;

D –  количество агрегатов на полной регулировке;

F –   количество агрегатов, прошедших первичную регулировку (60%) и ожидающих вторичной регулировки в накопителе;

E –  количество агрегатов в накопителе – агрегаты, не прошедшие первичную регулировку (40%);

Z –  общее количество агрегатов, прошедших регулировку;

ta –  время до прихода следующей партии агрегатов;

tb –  время, оставшееся до конца первичной регулировки;

tc –  время, оставшееся до конца вторичной регулировки;

td –  время, оставшееся до конца полной регулировки;

ts –  общее время регулировки.

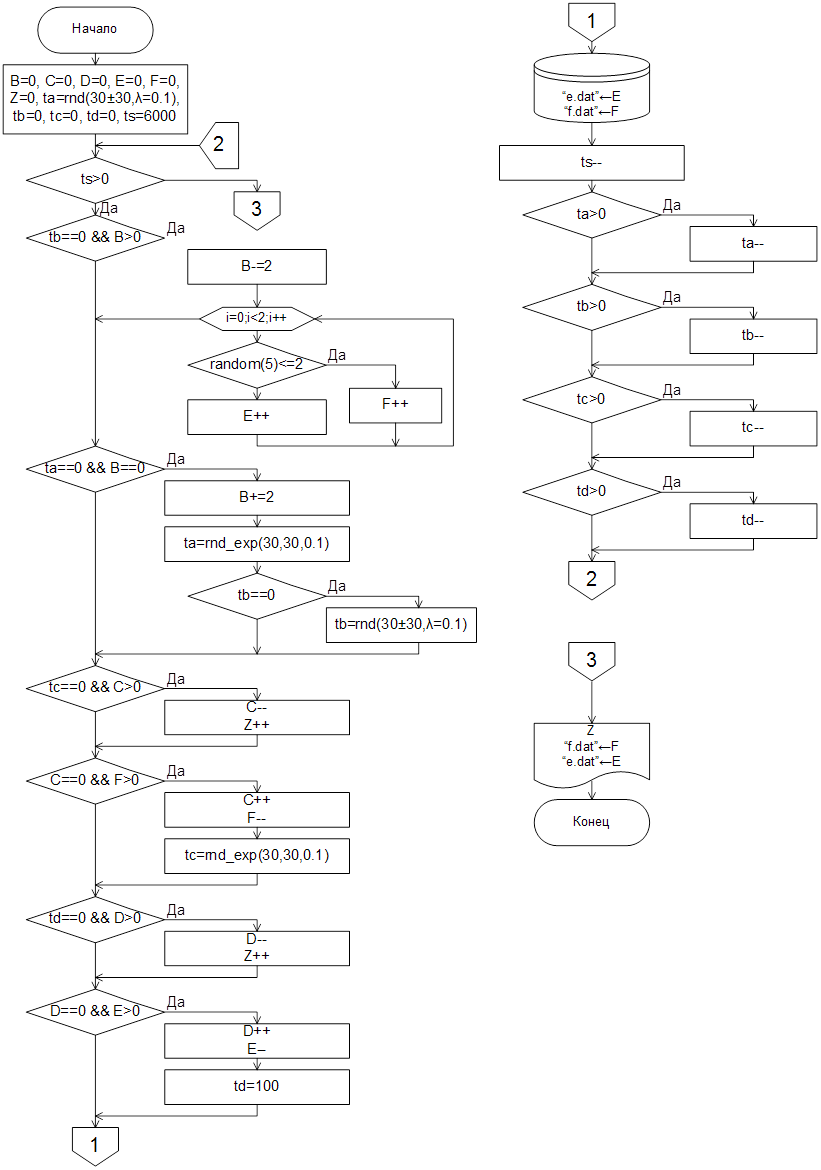
Рисунок 3 – Блок-схема рекуррентного алгоритма моделирования процесса во времени

Выполнение программы, моделирующей процесс

По блок-схеме алгоритма, с учётом требований языка, можно составить структуру модуля main(). Её анализ показывает, что для правильной работы необходимы две включаемые функции:

функция расчёта случайного числа по экспоненциальному закону распределения вероятности, которая возвращает целое число в зависимости от трёх аргументов: a – среднего значения, b – максимального отклонения, L – коэффициента λ, характеризующего параметры функции распределения вероятности;

функция (подпрограмма) построения графика значений из заданного файла, которая автоматически рассчитывает масштаб, количество точек, пределы изменения параметра, записанного в файл в виде значений через запятую.

Результаты работы программы показаны на рисунках 4 и 5.

Листинг программы:

#include <graphics.h>

#include <fstream.h>

#include <conio.h>

#include <stdio.h>

#include <stdlib.h>

#include <math.h>

int rnd_exp(double a, double b, double L);

void gr_file(char *fn);

void main()

{

     int B=0,C=0,D=0,E=0,F=0,Z=0;

     double    ta=rnd_exp(30,30,0.1),

               tb=0,tc=0,td=0,ts=60000;

     char zpt=',';

     char *fn1="e.dat";

     char *fn2="f.dat";

     fstream f1,f2;

     f1.open(fn1,ios::out);

     f2.open(fn2,ios::out);

     randomize();

     while(ts>0){

          if(tb==0 && B>0){

               B-=2;

               for(int i=0;i<2;i++){

                    if(random(5)<=2)F++;else E++;

               }

          }

          if(ta==0 && B==0){

               B+=2;

               ta=rnd_exp(30,30,0.1);

               if(tb==0)tb=rnd_exp(30,30,0.1);

          }

          if(tc==0 && C>0){

            C--; Z++;

          }

          if(C==0 && F>0){

               C++; F--;

               tc=rnd_exp(30,30,0.1);

          }

          if(td==0 && D>0){

            D--; Z++;

          }

          if(D==0 && E>0){

               D++; E--;

               td=100;

          }

          f1<<E<<zpt; f2<<F<<zpt;

          ts--;

          if(ta>0)ta--;

          if(tb>0)tb--;

          if(tc>0)tc--;

          if(td>0)td--;

     }

     f1.close();

     f2.close();

     gr_file(fn1);

     gr_file(fn2);

}

void gr_file(char *fn)

{

   int dr = DETECT, mod =1;initgraph (&dr,&mod,"");

   char zpt;

   fstream f;

   f.open (fn,ios::in);

   double a,n=0, max=-1e300,min=1e300;

   while(f.peek() != EOF)

       {

       f >> a >> zpt;n++;

       if (max < a) max = a;

       if (min > a) min = a;

      }

   if (max == min) {max++;min--;}

   f.close();

   cout.precision(2);

   setcolor(8);

   for (int i=0;i<=10;i++)

      {

       line (40,i * 38,620,i * 38);

      gotoxy(1,i*2.4+1);cout << max - i*(max-min)/10;

      line (40+i*58,0,40+i*58,380);

      gotoxy(4+i*7.2,25);printf("%0.0f", n*i/10);

      }

   gotoxy(2,25);cout << "N=";

   double k = 380/(max -min);

   double d = 380 - max * k;

   setcolor(14);

   if (0 < d && d< 380)

      {

      moveto(30,380-(int)d);

      outtext("0");

      line(40,380-(int)d,620,380-(int)d);

       }

   setcolor(12);

   f.open (fn,ios::in);

   double t=0;

   while(f.peek() != EOF)

      {

      f >> a >> zpt;

      int  y1 =(int) 380 - (a*k+d);

     int  x1 = t * 580. / n+40;

     if (t == 0) moveto(x1,y1);

     else

     lineto (x1,y1);

      t++;

      }

   setcolor(15);

   outtextxy(200,450,"Press any key to continue");

   getch();

   f.close();

   closegraph();

}

int rnd_exp(double a, double b, double L)

{

     ++b;

     double fd=10000;

     double k=exp(0)-exp(-L);

Q:   double c=random(b);

     double d=random(fd)/fd;

     double p=exp(-L*c)-exp(-L*(c+1));

     if(d<=p/k) if(random(2)==1) return (c+a); else {

          if(c==0)goto Q;     else return (-c+a);

     }

     goto Q;

}

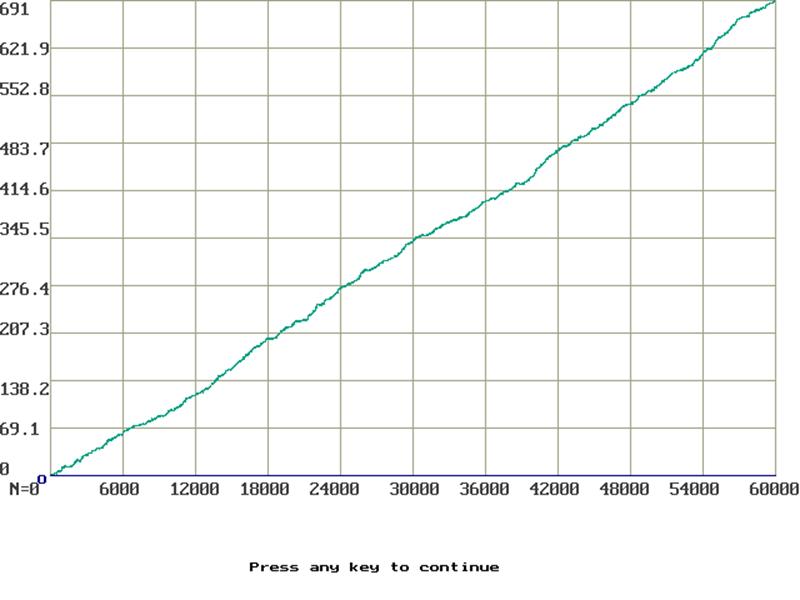
Рисунок 4 – График изменения значения переменной E(t) до оптимизации

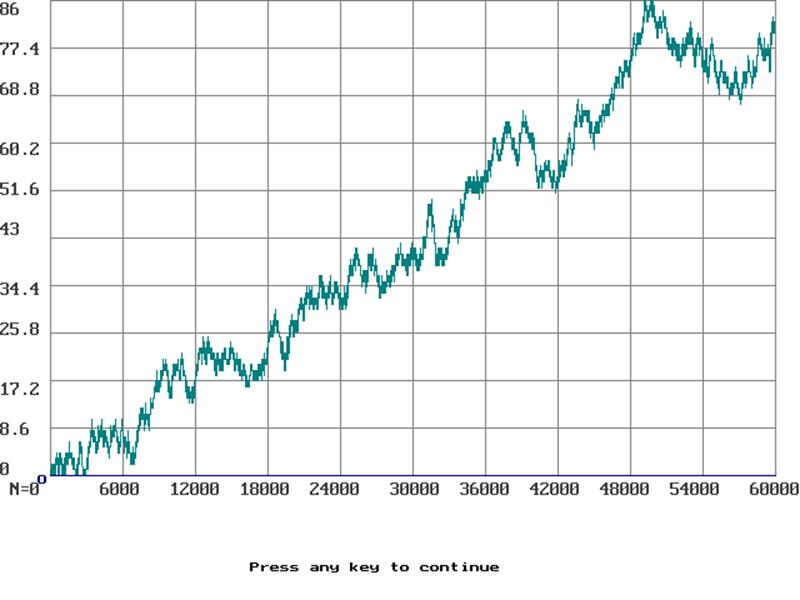
Рисунок 5 – График изменения значения переменной F(t) до оптимизации