





Лекция 3.
1. Программирование СУ в переменных состояния.
2. Прямое программирование.
3. Последовательное программирование.
4. Параллельное программирование.
5. Пример программирования.
6. Наблюдаемость и управляемость в СУ.
7. Пояснения по матрицам A, B, C, D в MATLAB.
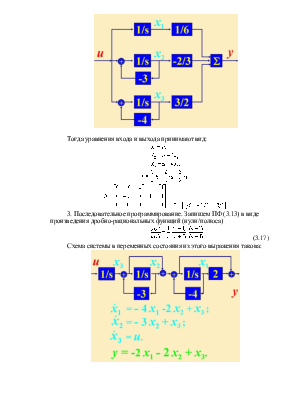
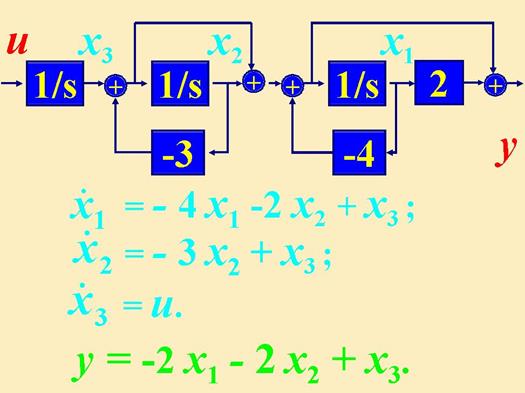
Для определения переменных состояния часто используют схему системы в этих переменных .
Она составляется из интеграторов, усилителей, суммирующих устройств. Выходы интеграторов выбирают в качестве координат (переменных) состояния. Такая схема дает наглядную физическую интерпретацию координат системы и описывает их взаимную связь.
Схемы в переменных состояния для непрерывных СУ
Они совпадают со схемами моделирования этих систем на АВМ. Схема СУ в переменных состояния может быть составлена по ПФ тремя способами:
1) прямого программирования,
2) параллельного программирования,
3) последовательного программирования.
Рассмотрим систему с ПФ:
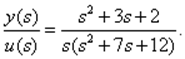 (3.13)
(3.13)
1. Прямое программирование. Разделив (3.13) на s3 , запишем
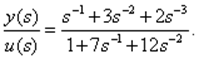
Обозначая
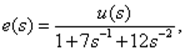 (3.14)
(3.14)
получим
![]()
![]()
На основе уравнений (3.14) и (3.15) схема в переменных состояния для заданной системы будет иметь следующий вид:
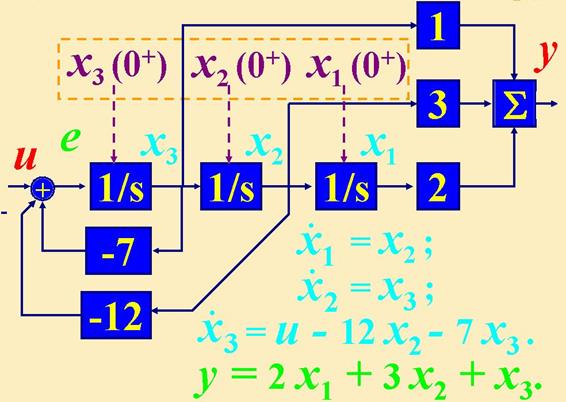
Полученные уравнения состояния и выхода можно расписать более полно:
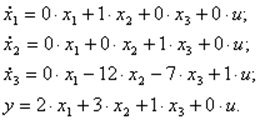
Тогда согласно схеме и уравнениям
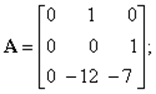
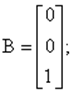
![]()
![]()
2. Параллельное программирование. Запишем ПФ (3.13) в виде суммы дробнорациональных функций:
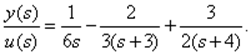 (3.16)
(3.16)
Схема системы в переменных состояния вытекает из этого выражения непосредственно
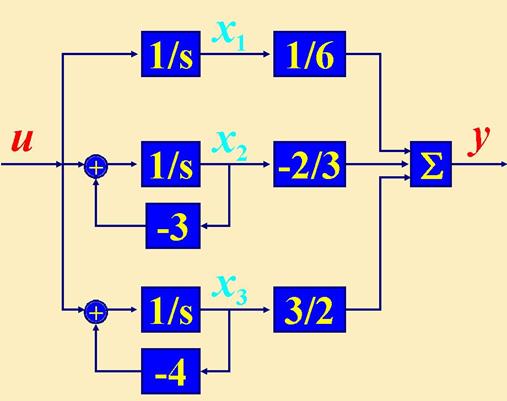
Тогда уравнения входа и выхода принимают вид:
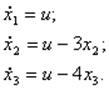
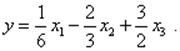
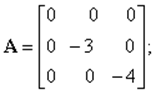
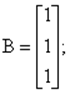
![]()
3. Последовательное программирование. Запишем ПФ (3.13) в виде произведения дробно-рациональных функций (нули/полюса)
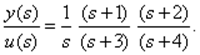 (3.17)
(3.17)
Схема системы в переменных состояния из этого выражения такова:
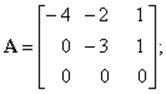
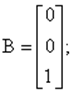
![]()
![]()
Пример
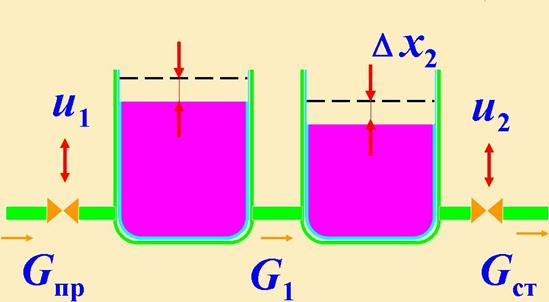
Рассмотрим систему из двух емкостей. Входные воздействия - перемещения клапанов на притоке жидкости u1(t) и стоке u2(t) , выходная величина - уровень жидкости во второй емкости y (t) = x2(t) . Для отрезка времени D tуравнение материального баланса любого бака имеет вид
![]()
где F- площадь сечения бака.
Для системы из двух емкостей при D t® 0 уравнения баланса таковы:
![]()
![]() (3.18)
(3.18)
Расход жидкости зависит от перепада давления на клапанах (м) и степени их открытия u
![]()
![]()
![]() (3.19)
(3.19)
где P0пр и P0ст - давления на притоке перед клапаном и на стоке после клапана, м. Они постоянны. При подстановке (3.19) в (3.18) получим систему нелинейных уравнений состояния. Их можно линеаризовать.
Тогда при x01 = 2 м, x02 = 1 м, P0пр = 6 м, P0ст = 0, u01 = u02 = 0,5 и F1 = F2 = 1 м2, получим
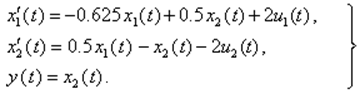 (3.20)
(3.20)
Исключением переменных состояния x1(t) и x2(t) система уравнений (3.20) приводится к уравнению 2-го порядка
![]()
Теперь найдем матричную ПФ, отвечающую системе уравнений (3.20).
Матрицы уравнений в ПС таковы:
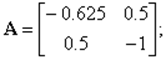
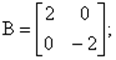
![]()
![]()
Отсюда
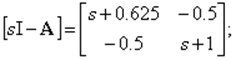
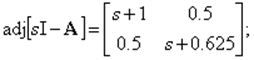
![]()
Обратная матрица равна
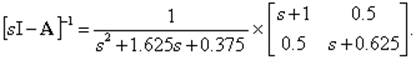
Откуда ПФ в матричном виде равна
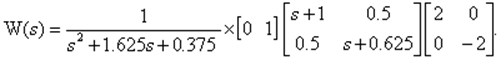
или
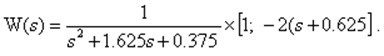
Таким образом, ПФ по каналам действия u1(t) и u2(t)
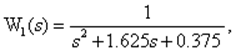
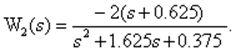
При определении уравнений состояния по уравнению «вход-выход» реальной динамической системе можно поставить в соответствие несколько моделей, адекватно воспроизводящих вход и выход реальной системы, но имеющих разную внутреннюю структуру. Если по такой модели (из ДУ «вход-выход») можно восстановить ее внутреннюю структуру, система называется наблюдаемой.
Ненаблюдаемость системы возникает обычно, если в ПФ есть одинаковые и потому сокращаемые сомножители. В результате число уравнений состояния модели оказывается меньше числа уравнений состояний системы.
Поэтому ДУ состояния обычно содержат более полную информацию о реальной динамической системе, чем ее ПФ.
В соответствии с критерием Р.Калмана ОУ полностью управляем, если и только если блочная матрица nx nm
Qу = [B, AB, A2 B, … , An– 1B ]
имеет ранг размерности nпространства состояний, т.е. если rank Qу = n.
Ранг матрицы находится как наибольший порядок отличных от нуля квадратных миноров матрицы.
Ранг матрицы Qу равен числу ее линейно независимых столбцов.
Если В матрица-столбец, то для пол-ной управляемости необходимо, чтобы квадратная матрица управляемости Qу была невырожденной, т.е. чтобы ее определитель det Qу ¹ 0.
Если A диагональная матрица и все ее элементы различны, то для управляемости нужно, чтобы матрица В не содержала нулевых строк.
Если ранг матрицы Qу меньше n, то ОУ не полностью управляемый.
Система, описываемая уравнением выхода,
![]()
называется полностью наблюдаемой, если по данным измерения или наблюдения векторов y(t) и u(t) на конечном интервале времени t0 < t< t1 можно однозначно определить (восстановить) начальное состояние x(t0).
В соответствии с критерием Р.Калмана ОУ полностью наблюдаем, если и только если блочная матрица nx nm
Qн =[Ст, AтСт, (Aт)2Ст,…, (Aт)n – 1 Ст]
имеет ранг размерности nпространства состояний, т.е. если
rank Qн = n.
Если ранг матрицы наблюдаемости меньше n, то ОУ не полностью наблюдаемый.
Если матрица С состоит лишь из одной строки, то для наблюдаемости необходимо и достаточно, чтобы квадратная матрица Qн была невырожденной , т.е. чтобы ее определитель det Qн ¹ 0..
Если A диагональная матрица и все ее элементы различны, то для наблюдаемости необходимо, чтобы матрица С не содержала нулевых столбцов.
Для установления управляемости и наблюдаемости СУ существуют различные вычислительные процедуры, в том числе и на ЭВМ.
Для их понимания и использования необходимо хорошо знать свойства матриц, их преобразование и вычисление.
MATLAB 7
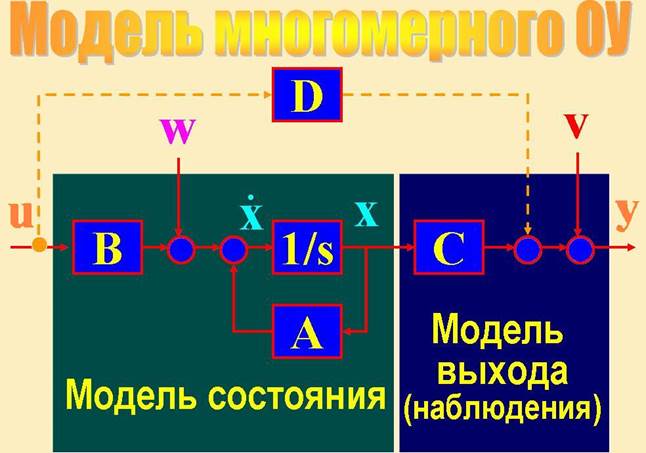
Пояснения по матрицам A, B, C, D, получаемым в MATLAB в методе пространства состояния.
Команда ss в MATLAB
Преобразуем ПФ (3.13) из примера последовательного программирования СУ в ПС
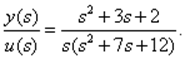
с помощью MATLAB. Для этого введем:
h= tf ([1 3 2],[1 7 12 0] );
h1 = ss (h)
MATLAB выдаст матрицы А, B, C, D
![]()
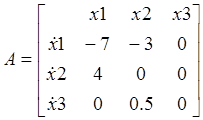
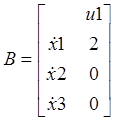
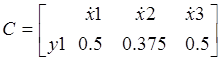
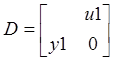
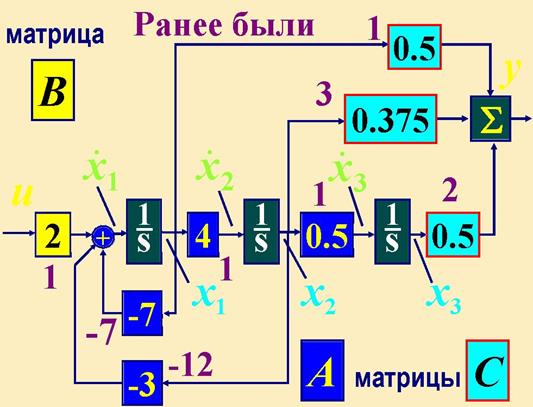
В MATLAB переменные состояния расположены в порядке убывания производных, т.е. от входа uидет х1, х2, х3, а не в обычном порядке х3, х2, х1.
Модель СУ в MATLAB строится методом прямого программирования.
Если использовать матрицы A, B, C, D других методов программирования, то результат перехода к ПФ вида TF будет один и тот же, а именно (3.13).
Уравнения модели СУ в ПС для рассматриваемого примера таковы:
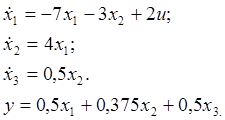
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.