Построение графика математической функции в заданном диапазоне

Цель работы: Получить навыки программирования ПЭВМ на языке С++. Научиться решать прикладные задачи, изучить особенности  практической реализации известных алгоритмов на языке Borland C++ 3.1, являющимся одним из наиболее часто применяемых языков программирования современных персональных и промышленных ЭВМ, входящих в состав АСУТП.

Задание

1.  Написать программу расчёта 512 точек функции в указанном диапазоне. Результат оформить в виде таблицы. Таблицу вывести на экран и записать в файл.

2.  Построить график функции на указанном диапазоне.

3.  Найти все нули функции.

Заданная математическая функция имеет вид:

,

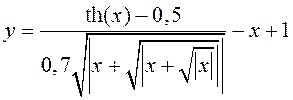в диапазоне [-1,5; 2].

Выполнение работы

Блок-схемы алгоритмов программы:

1.  Подпрограмма f_y(doublex) расчёта значения функции в точке x.

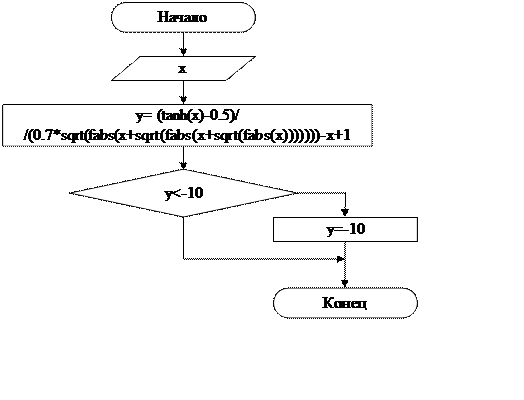
Рисунок 1 – Подпрограмма нахождения значения функции в точке x

2.  Подпрограмма расчёта 512 точек функции.

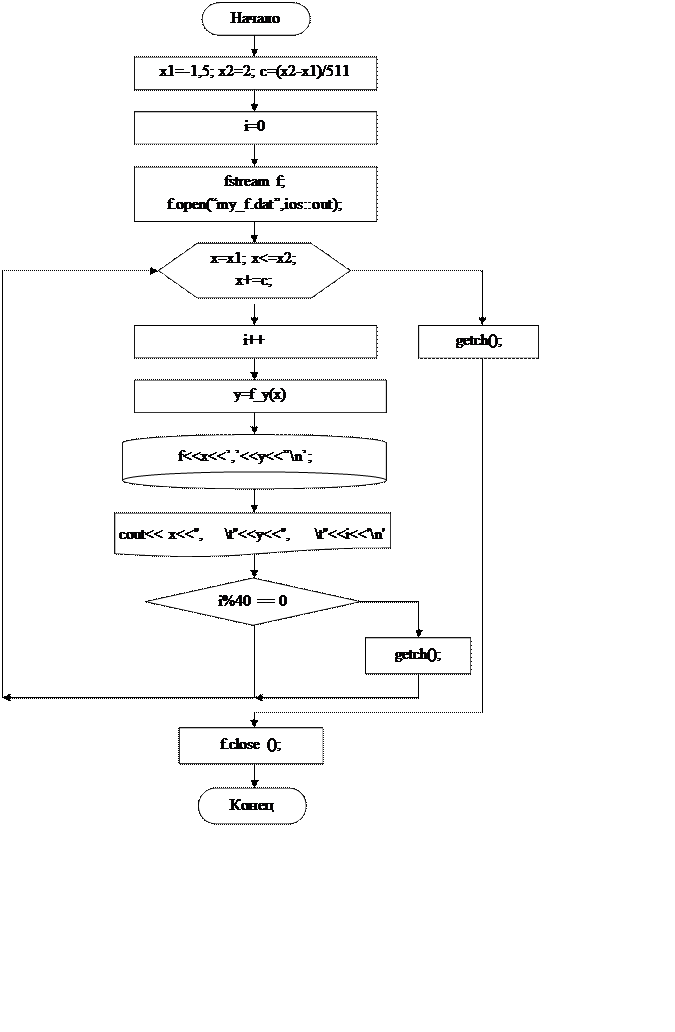
Рисунок 2 – Подпрограмма расчёта 512 точек функции

3.  Программа построения графика функции.

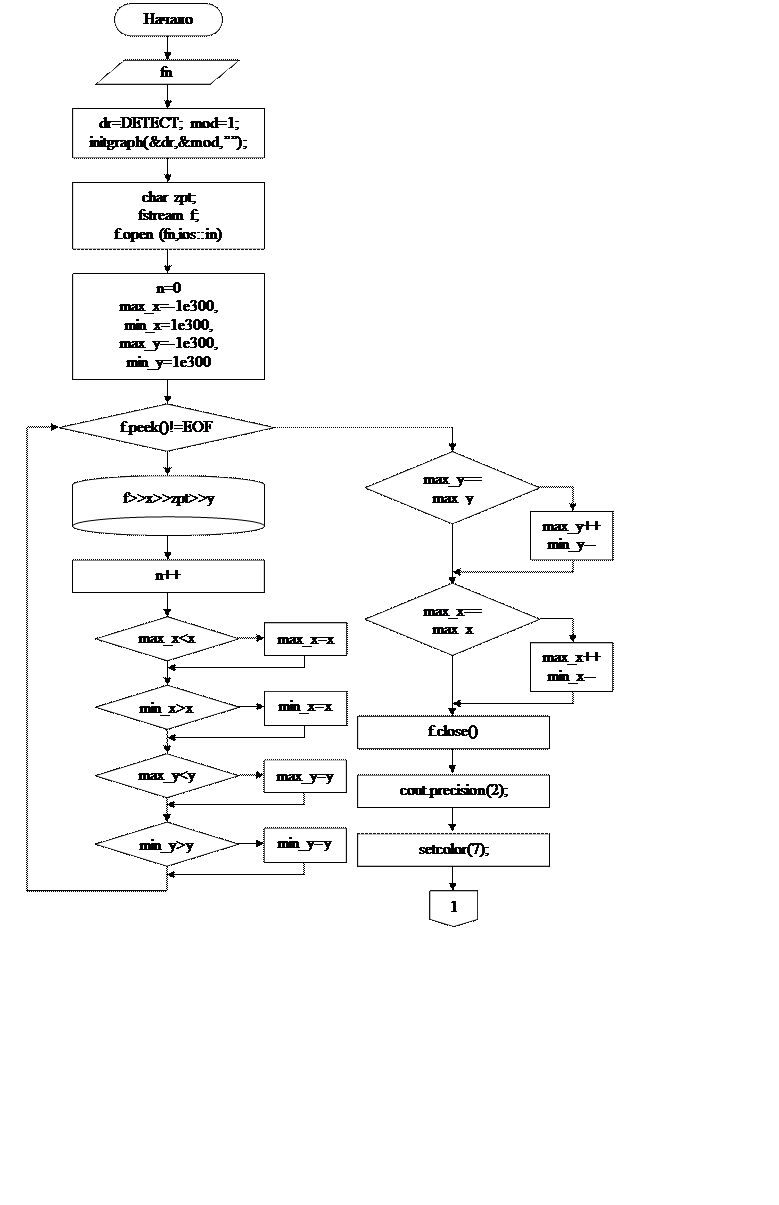
Рисунок 3 – Программа построения графика функции

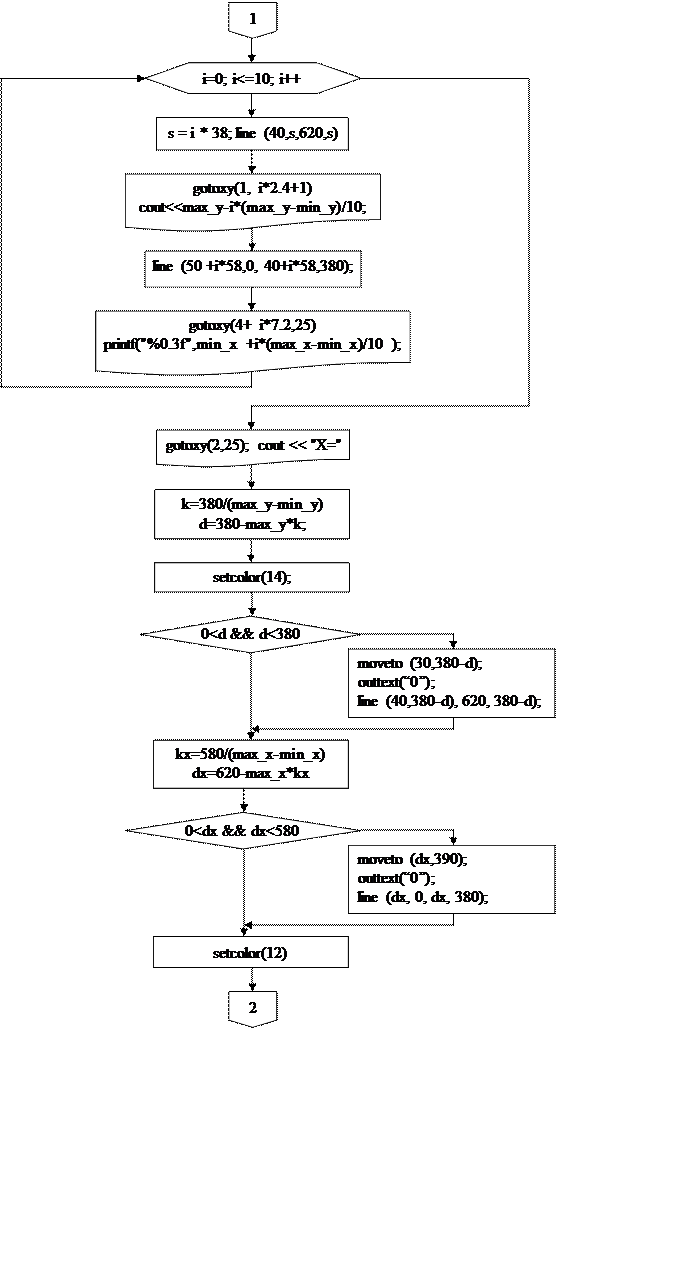
Рисунок 3 – Продолжение

y1=380-(y*k+d); x=t*580/n; x1=x+40;

lineto(x1,y1);

moveto(x1,y1);

t++;

f.open (fn,ios::in)

t=0

setcolor(13)

xr1 = zero(-1,0.5)

xr2 = zero(0.01,1)

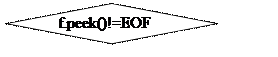
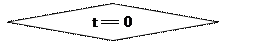
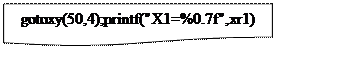
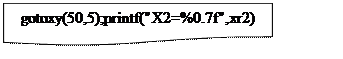
Рисунок 3 – Продолжение

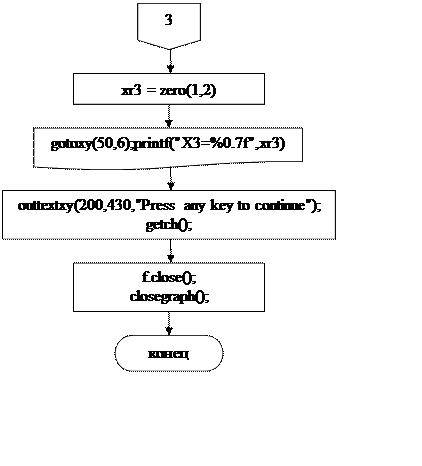
Рисунок 3 – Окончание

4.  Подпрограмма zero(doublex1, doublex2) нахождения нулей функции

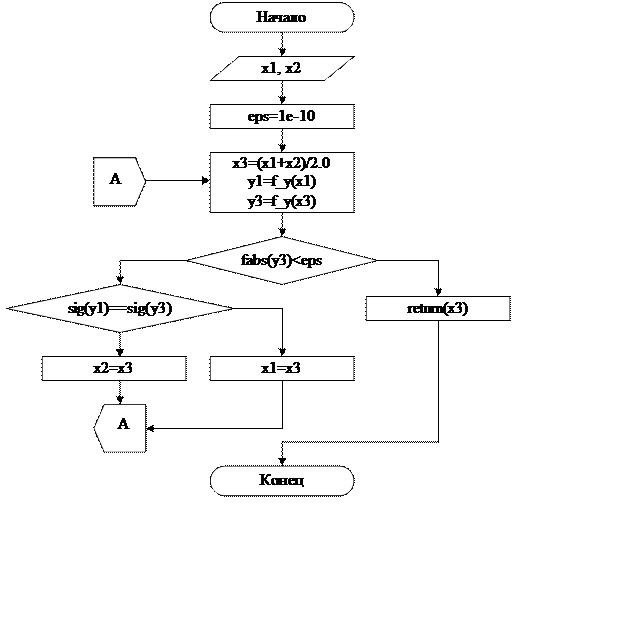
Рисунок 4 – Метод деления на 2 с оценкой результата по знаку y(x)

5.  Подпрограмма sig(y). Осуществляет определение знака функции.

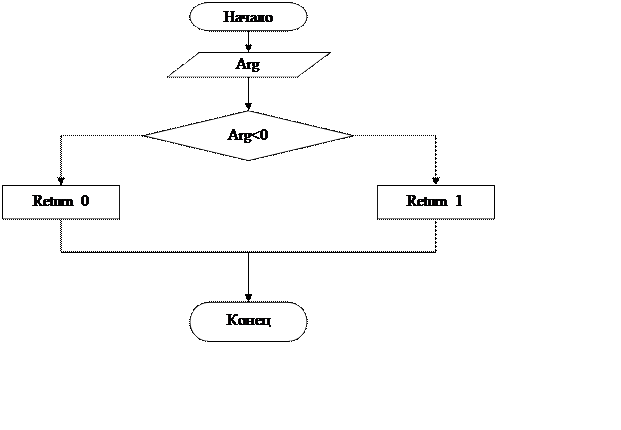
Рисунок 5 – Метод деления на 2 с оценкой результата по знаку y(x)

Листинг файла LAB1_V05.CPP:

#include <graphics.h>

#include <iostream.h>

#include <fstream.h>

#include <conio.h>

#include <stdio.h>

#include "gr_lab05.cpp"

#include <math.h>

void main(void)

{

double f_y(double);

double x1 =-1.5,x2=2,c=(x2-x1)/512.0;

int i=0;

fstream f;

f.open("my_f.dat",ios::out);

for (double x=x1;x<=x2;x+=c)

 {

  i++;

  double y = f_y(x);

  f<< x<<','<<y<<'\n';

  cout<< x<<",     \t"<<y<<",     \t"<<i<<'\n';

  if(i%40==0)getch();

 }

getch();

f.close();

gr("my_f.dat");

}

double f_y(double x)

{

 double y;

 y=(tanh(x)-0.5)/(0.7*sqrt(fabs(x+sqrt(fabs(x+sqrt(fabs(x)))))))-x+1;

 if(y<-10)y=-10;

 return y;

}

double zero(double x1,double x2)

{

double sig(double);

double f_y(double);

double x3,y1,y3,eps=0.0000001;

A:

x3=(x1+x2)/2.0;

y1 = f_y(x1);

y3 = f_y(x3);

if (fabs(y3)<eps) return x3;

else

     {if (sig(y1)==sig(y3)) x1=x3;

              else x2=x3;}

goto A;

}

double zero1(double x1, double x2)

{

double f_y(double);

double grad_f(double);

double x3,y1,y3,eps=0.0000001;

A:

x3=(x1+x2)/2.0;

y3 = f_y(x3);

if (fabs(y3)<eps) return x3;

else

     {if (grad_f(x1)==grad_f(x3)) x1=x3;

              else x2=x3;}

goto A;

}

double grad_f(double x)

{

double f_y(double);

double y1,y2,eps=0.0000001;

y1=f_y(x);

y2=f_y(x+eps);

if (y1<y2) return 1.; else return 0.;

}

double sig(double arg)

{

if (arg<0) return 1.; else return 0.;

}

Листингфайла GR_LAB05.CPP:

void gr(char *fn)

{ // инициализация графического режима

double zero(double,double);

double zero1(double,double);

int dr = DETECT, mod =1;initgraph (&dr,&mod,"");

char zpt;

fstream f;

f.open (fn,ios::in);

double x,y,n=0, max_x=-1e300,min_x=1e300, max_y=-1e300,min_y=1e300;

while(f.peek() != EOF)

 {

  f >> x >> zpt>>y;n++;

  if (max_x < x) max_x = x;

  if (min_x > x) min_x = x;

  if (max_y < y) max_y = y;

  if (min_y > y) min_y = y;

 }

if (max_y == min_y) {max_y++;min_y--;}

if (max_x == min_x) {max_x++;min_x--;}

f.close();

cout.precision(3);

 //Построение графика (оси)

setcolor(8);

//gotoxy(10,10);cout<<n;

for (int i=0;i<=10;i++)

 {int s = i * 38;

  line (40,s,620,s);

  gotoxy(1,i*2.4+1);cout << max_y - i*(max_y-min_y)/10;

  line (40+i*58,0,40+i*58,380);

  gotoxy(4+i*7.2,25);printf("%0.3f",min_x +i*(max_x-min_x)/10 );

 }

gotoxy(2,25);cout << "X=";

double k = 380/(max_y -min_y);

double d = 380 - max_y * k;

setcolor(14);

if (0 < d && d< 380) {moveto(30,380-(int)d);

               outtext("0");

               line(40,380-(int)d,620,380-(int)d);

              }

double kx = 580/(max_x -min_x);

double dx = 620 - max_x * kx;

if (0 < dx && dx< 580) {moveto((int)dx,390);

               outtext("0");

               line((int)dx,0,(int)dx,380);

              }

setcolor(12);

//собственно, построение графика

f.open (fn,ios::in);

double t=0;

while(f.peek() != EOF)

 {f >> x >> zpt>>y;

  int  y1 =(int) 380 - (y*k+d);

  double x = t * 580. / n;

  int  x1 =(int) x+40;

  if (t == 0) moveto(x1,y1);

  else lineto (x1,y1);

  t++;

 }

setcolor(13);

double xr1 = zero(-1,-0.5);

gotoxy(50,4);printf("X1=%0.7f",xr1);

double xr2 = zero(0.01,1);

gotoxy(50,5);printf("X2=%0.7f",xr2);

double xr3 = zero(1,2);

gotoxy(50,6);printf("X3=%0.7f",xr3);

outtextxy(200,430,"Press any key to continue");

getch();f.close();closegraph();

}

Результаты работы программы

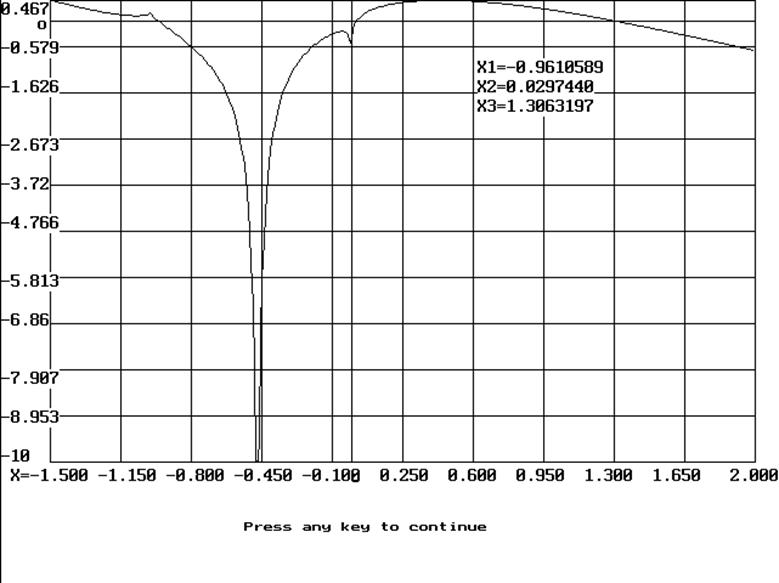
Рисунок 6 – График функции и нули функции

Вывод

При проведении данной лабораторной работы были получены навыки программирования ПЭВМ на языке С++. В ходе работы были получены умения решать прикладные задачи, изучены особенности практической реализации известных алгоритмов на языке Borland C++ 3.1, являющимся одним из наиболее часто применяемых языков программирования современных персональных и промышленных ЭВМ, входящих в состав АСУТП.