«Институт Цветных Металлов и Материаловедения»
Федеральное государственное образовательное учреждение высшего профессионального образования
Сибирский Федеральный Университет
Институт (факультет) ИМ
Кафедра автоматизации
Специальность АМЦ
Группа 06-2
Лабораторная работа
(Моделирование и оптимизация)
Преподаватель _______________
(подпись, дата)
Разработали студенты _______________ Харитонова О.Н.
(подпись, дата)
Красноярск, 2008
Вариант-5
Определить зависимость механических свойств бронзы Бр.ОФ4-0,5 (наклеп 60%) от температуры отжига. Спрогнозировать относительное удлинение d, % и предел прочности при растяжении sв, кгс/мм2, при 750°С.
|
Предел прочности |
67 |
66 |
65 |
60 |
46 |
36 |
35 |
33 |
31 |
|
Относительное удлинение |
5 |
4 |
5 |
12 |
31 |
49 |
51 |
52 |
53 |
|
Температура отжига, °С |
0 |
100 |
200 |
300 |
350 |
400 |
500 |
600 |
700 |
1) Найдём зависимость предела прочности от температуры отжаги.
У-предел прочности
Х-температура отжига
|
y |
x |
Теор.знач-е y |
dy |
|
67 |
0 |
66,504 |
-0,496 |
|
66 |
100 |
68,514 |
2,514 |
|
65 |
200 |
63,524 |
-1,476 |
|
60 |
300 |
54,534 |
-5,466 |
|
46 |
350 |
49,4765 |
3,4765 |
|
36 |
400 |
44,544 |
8,544 |
|
35 |
500 |
36,554 |
1,554 |
|
33 |
600 |
33,564 |
0,564 |
|
31 |
700 |
38,574 |
7,574 |
Теперь построим график зависимости предела прочности от температуры отжига Также построим на данном графике линию тренда. И по графику вычислим уравнение У и квадрат коэффициента корреляции. По этому коэффициенту можно судить о том, что модель может быть использована для предсказания результатов.
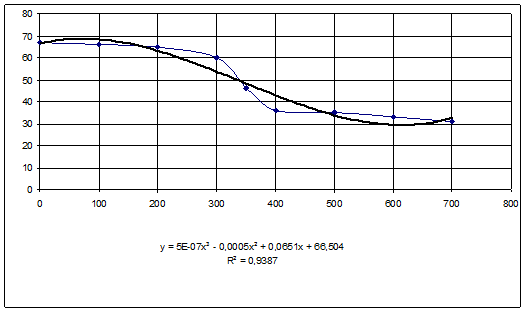
После построения графика зависимости, следует проверить модель на адекватность. Мы будем использовать метод построения гистограммы распределения остатков модели. Для этого находим на интервале максимальное и минимальное значения dy. После нахождения этих значений весь диапазон изменения остатков разбиваем на несколько равных поддиапазонов и рассчитываем число попаданий остатков (ошибки) в каждый из этих поддиапазонов. Затем строим гистограмму.
|
Карман |
Частота |
Интегральный % |
|
|
-5,2 |
1 |
11,11% |
|
|
-2 |
0 |
11,11% |
|
|
-0,5 |
1 |
22,22% |
|
|
1,6 |
3 |
55,56% |
|
|
3,5 |
2 |
77,78% |
|
|
7,5 |
0 |
77,78% |
|
|
8,6 |
2 |
100,00% |
|
|
Еще |
0 |
100,00% |
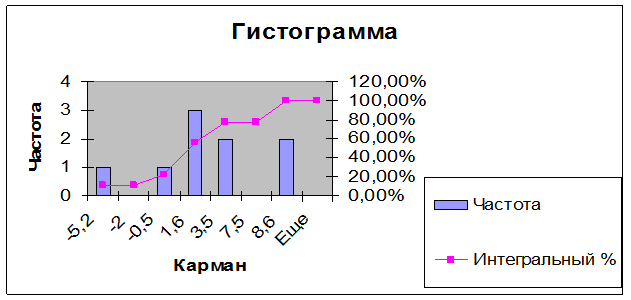
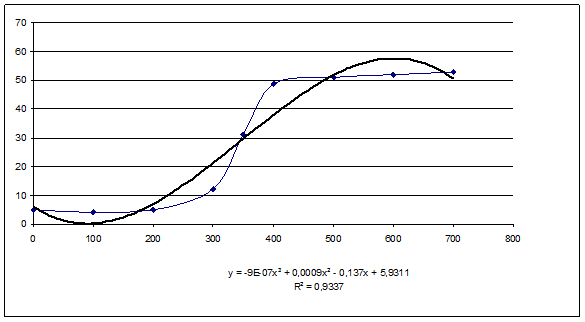
2) Таким же образом,как и в случае до этого, найдём зависимость относительного удлинения от температуры отжига.
У-относительное удлинение
Х-температура отжига
|
у |
х |
терет.знач-е у |
dy |
|
0 |
5 |
5,9311 |
0,311 |
|
100 |
4 |
0,3311 |
-3,6689 |
|
200 |
5 |
7,3311 |
2,3311 |
|
300 |
12 |
21,5311 |
9,5311 |
|
350 |
31 |
29,6436 |
-1,3564 |
|
400 |
49 |
37,5311 |
-11,4689 |
|
500 |
51 |
49,9311 |
-1,0689 |
|
600 |
52 |
53,3311 |
1,3311 |
|
700 |
53 |
42,3311 |
-10,6689 |
|
Карман |
Частота |
Интегральный % |
|
|
-11,2 |
1 |
11,11% |
|
|
-9,5 |
1 |
22,22% |
|
|
-5,5 |
0 |
22,22% |
|
|
-2 |
1 |
33,33% |
|
|
1,5 |
4 |
77,78% |
|
|
3,5 |
1 |
88,89% |
|
|
9,6 |
1 |
100,00% |
|
|
Еще |
0 |
100,00% |
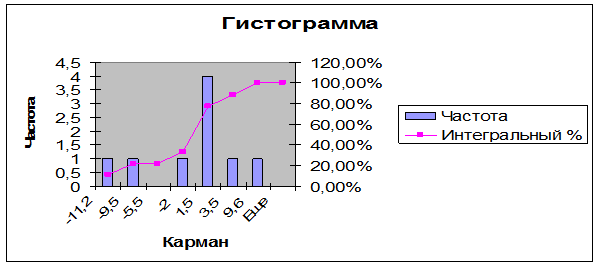
Вывод: Мы исследовали методику решения задач нахождения коэффициентов регрессионной модели. С помощью средства поиска решений, решена задача нахождения уравнения рецессии для одной зависимой и одной независимой переменных. Хотя рассмотренная модель имеет очень специфический вид, описанный подход позволяет исследовать любое уравнение регрессии. Мы вычислили характеристики линейного уравнения регрессии, которые позволяют значительно упростить процедуру регрессионного анализа для этих наиболее часто встречающихся на практике моделей.
В своей работе я создавала математические модели, с помощью которых выявляла зависимость некоторых физических свойств модели от температуры и времени, проверяла созданную модель на адекватность с помощью метода остроения гистограммы. Об адекватности можно судить по коэффициенту корреляции, гистограмме распределения остатков. Также с помощью построенных линий тренда получила уравнение, которое помогло спрогнозировать дальнейшее поведение модели и её свойства.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.