Антенна для РЛС обнаружения, страница 6

После выбора размеров волновода можно определить длины рупора по формулам (4) и (5). Из (4) рассчитывают одну из длин и через (5) вычислить длину в другой плоскости.

Рассчитаем длину рупора в Е плоскости:  .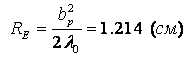

Затем через (5) определяем длину в H плоскости:

.

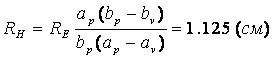Проверяем удовлетворяет ли значение  условию оптимальности (4), т.е. . Получаем, что по условию , т.е. при  условие соблюдается. Тогда .

Теперь необходимо проверить обеспечивают ли данные размеры рупора  допустимый уровень квадратичных фазовых ошибок, которые должны удовлетворять следующим условиям (из [2]):

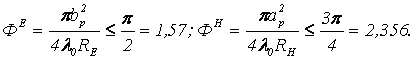                           (6)

По формулам (6) получим:  и , что вполне удовлетворяет допускам.

Произведем расчет реальной ДН рупора:

1) Расчет реальной ДН рупора в Н плоскости

Расчет начинаем с Н плоскости, т.к. ДН в ней зависит только от одного размера .

Реальную ДН в Н плоскости можно определить по следующей формуле :

.

где 

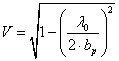
 – модуль коэффициента отражения волны от раскрыва рупора;

Для наглядности пронормируем реальную ДН, то есть поделим на F_p^H(Ψ) при Ψ=0. Размер  подбирается так, чтобы разница между реальной ДН  и идеальной  (рис.4) была минимальной и не превышала 7-9 %. Полученные совмещенные графики реальной, идеальной ДН и их относительной ошибки (помноженной на 10) в Н плоскости представлены на рис.5.

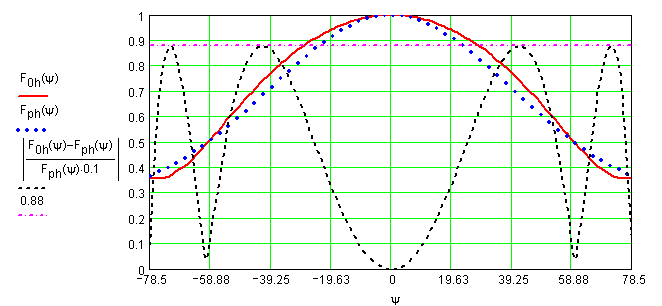
Рис.5 График реальной ДН облучателя в Н плоскости

Теперь аналогично рассчитаем реальную ДН облучателя в Е плоскости.

2) Расчет реальной ДН рупора в E плоскости

Реальную ДН в Е плоскости можно определить по следующей формуле из

[2]:

Пронормируем реальную ДН, то есть поделим на F_p^Е(Ψ) при Ψ=0.

ДН в этой плоскости зависит как от , так и от . Но т.к.  уже определен из расчета в Н плоскости, то изменяя только размер  рассчитываем реальную ДН рупора в Е плоскости (), так чтобы разница между ней и идеальной ДН  (рис.3) была минимальной и не превышала 7-9 %. Полученные совмещенные графики реальной, идеальной ДН и их относительной ошибки (помноженной на 10) в Е плоскости представлены на рис.6.