Зеркальные антенны, страница 2

В итоге получим формулу для прямой УБЛ:

УБЛ()=-29.8*-6.75;

Рис.2.График зависимости табличных значений УБЛ в близи уровня от величины скачка ноля на краю зеркала.

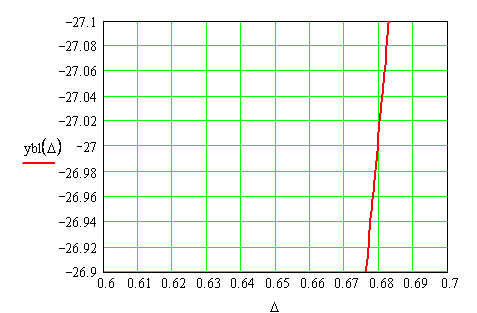
Табличные значения коэффициентов пропорциональности вблизи уровня по ТЗ:

, .

В итоге получим формулу для прямой :

.

Рис.3.График зависимости табличных значений коэффициентов пропорциональности в близи уровня от величины скачка поля на краю зеркала.

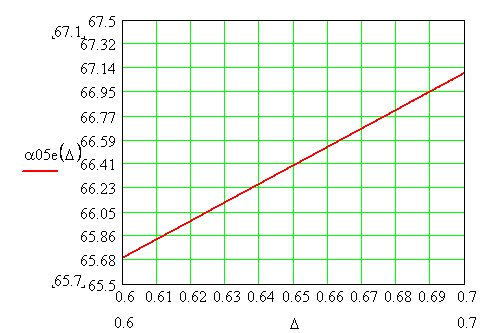
По графику UBL_i (D) находим скачок De = 0.68 обеспечивающий UBL_E = = - 27.0 дБ. Пользуясь этим значением D рассчитываем функцию Ee(x) и строим ее график.

Скачок поля в плоскости Е: .

Функция распределения амплитуды поля в раскрыве:

.

Рис.4.График зависимости функции Ее(х) от координаты точки в раскрыве зеркала.

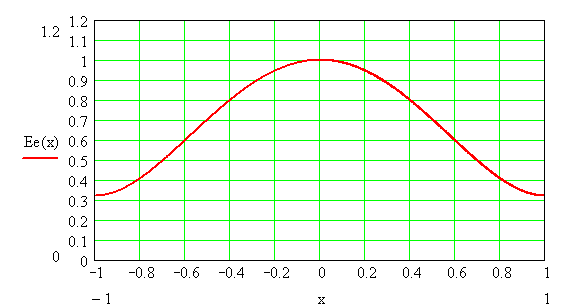
1.3. Расчет размеров раскрыва

После выбора распределения поля Eе(x) можно найти размеры раскрыва. Они зависят от , рабочей длины волны l и выбранных функций E(x_Н). Как известно, с увеличением размера раскрыва в какой либо плоскости ширина главного лепестка ДН в этой плоскости снижается (при неизменном распределении поля) , где a_0.5 коэффициент пропорциональности, a – размер раскрыва (для параболоида вращения а=2R).

Найдем размер круглого раскрыва в плоскости E. Из рис.3 находим . Далее, пользуясь заданными значениями частоты f₀ и ширины ДН, определяем размеры раскрыва.

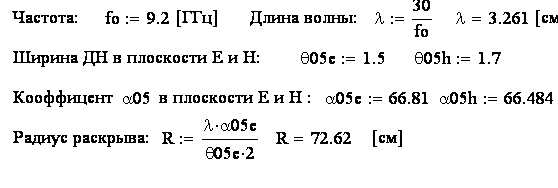
Расчитаем размеры (диаметры) зеркала:

.

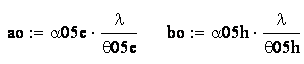
1.4. Расчет ДН облучателя

Распределение поля Е(x_H) в раскрыве зеркала легче всего определить методом геометрической оптики. В параболоиде врашения облучатель должен создавать сферическую волну. У такой волны амплитуда убывает с удалением r от источника (облучателя) обратно пропорционально r (в дальней зоне, в среде без потерь). После отражения от зеркала фронт волны становится плоским, а амплитуда плоской волны в среде без потерь не зависит от расстояния.

Поэтому можем записать связь ДН облучателя f(y) и поля в раскрыве Е(x_H) в виде  (с точностью до постоянного размерного множителя). Нормируя ДН на максимум , получим расчетную формулу для нормированной ДН облучателя (по напряженности)

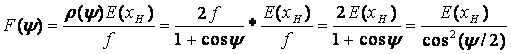    (2)

В формуле (2) координаты x_H нужно находить через угол y по соотношению вытекающему из (1):

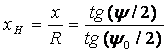       (3)

Для этого следует задаться углом раскрыва y₀, его значение обычно выбирают в пределах . Это дает возможность обеспечить в дальнейшем достаточно высокий КИП при сравнительно небольших размерах облучателя и, как следствие с меньшим затемнением зеркала.