Изучение методов спектрального анализа периодических сигналов, страница 2

4.1. Получим амплитудный спектр сигнала S₁

На интервале времени , равном периоду, заданную последовательность представим в виде

.

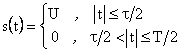Разложим сигнал в тригонометрический ряд Фурье. Коэффициент ряда

.

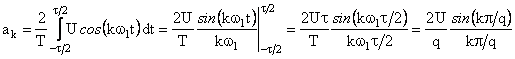Постоянная составляющая

.

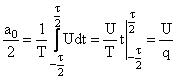Окончательно будем иметь

.

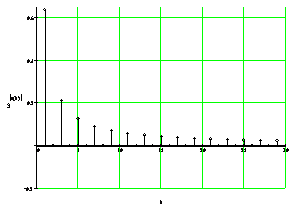
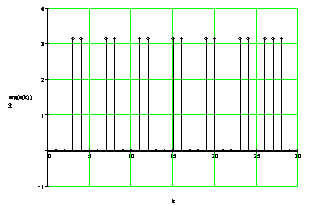
На рисунке 2 приведены периодическая последовательность прямоугольных импульсов, ее амплитудный и фазовый спектры.

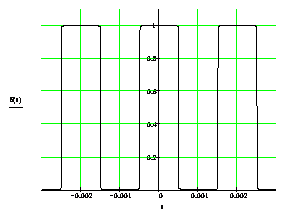
а)                                                                б)

в)

Рисунок 2 - Периодическая последовательность прямоугольных импульсов (а), ее амплитудный (б) и фазовый (в) спектры

4.2. Получим амплитудный спектр сигнала S₂

На интервале времени , равном периоду, заданную последовательность представим в виде

.

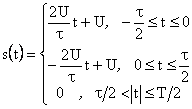Разложим сигнал в тригонометрический ряд Фурье. Коэффициент ряда

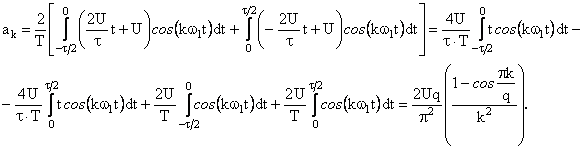
Постоянная составляющая

.

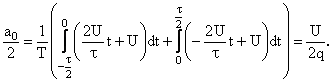Окончательно будем иметь

.

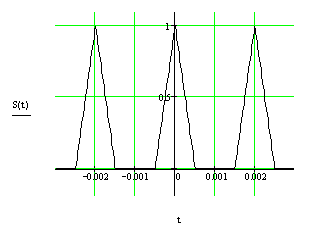
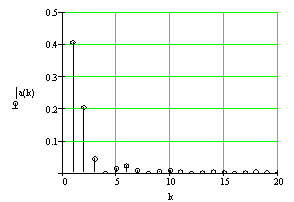
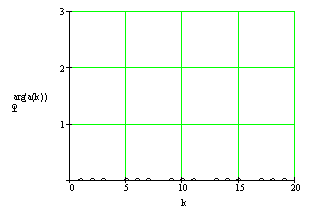
На рисунке 3 приведены периодическая последовательность прямоугольных импульсов, ее амплитудный и фазовый спектры.

а)                                                                б)

в)

Рисунок 3 - Периодическая последовательность треугольных импульсов (а), ее амплитудный (б) и фазовый (в) спектры

4.3. Получим амплитудный спектр сигнала S₃

На интервале времени , равном периоду, заданную последовательность представим в виде

.

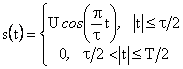Разложим сигнал в тригонометрический ряд Фурье. Коэффициент ряда

.

Постоянная составляющая

.

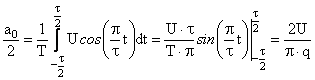Окончательно будем иметь

.

На рисунке 4 приведены периодическая последовательность прямоугольных импульсов (а), ее амплитудный (б) и фазовый (в) спектры.

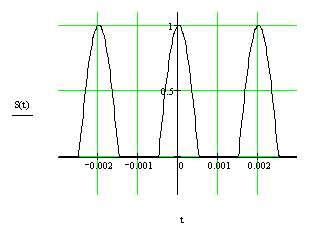
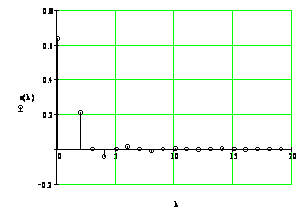
а)                                                                б)

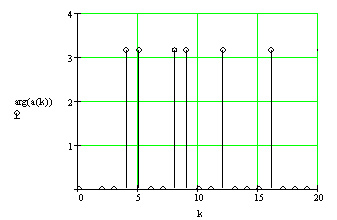
в)

Рисунок 4 - Периодическая последовательность косинусоидальных импульсов (а), ее амплитудный (б) и фазовый (в) спектры

5. Моделирование заданных сигналов и их спектральный анализ в пакете Electronics Workbench.

Для исследования используем схему, приведенную на рисунке 5.