Измерение параметров радиотехнических сигналов универсальным осциллографом: Руководство к лабораторной работе, страница 11

По интерференционной фигуре можно определить отношение частот по формуле:

f_г            n_в

------  =  ------ ,

f_в            n_г

где: f_г и f_в – частоты гармонических напряжений, приложенных к горизонтально-отклоняющим и к верти­кально-отклоняющим пластинам осциллографа соответственно; n_в – число касаний интерференционной фигурой одной вертикальной линии; n_г – число касаний интерференционной фигурой одной горизонтальной линии. Например, на рис. П.5 показана интерференционная фигура при  f_г = 1,5 f_в   (стрелками показаны точки касания фигурой условных вертикальной и горизонтальной линий).

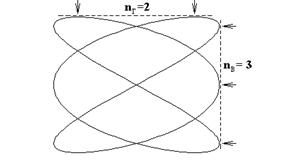
Рис. П.5

При измерении частоты методом интерференционных фигур гармоническое напряжение, частоту f_x которого надо измерить, подводят ко входу канала Y, а гармоническое напряжение с выхода образцового генератора – ко входу усилителя канала Х (можно подавать и наоборот).

Затем плавно изменяют частоту образцового генератора и добиваются такого ее значения f_o, при ко­тором интерференционная фигура будет «неподвижной». По этой фигуре определяют n_в и n_г. Так  как f_г = f_о, а f_в = f_x, то измеряемую частоту fx вычисляют по формуле

          n_г

f_x = f_о -----.

          n_в

Наиболее просто измерить частоту, если интерференционная фигура – эллипс (рис. П.3), получаю­щийся при равенстве сравниваемых частот (n_в = n_г = 1). В этом случае никаких вычислений не требуется, т.к. измеряемая частота просто считывается со шкалы настройки частоты образцового генератора.

Обычно «неподвижную» интерференционную фигуру получить трудно, а то и просто невоз­можно. Это объясняется следующим. Положим, что в течение некоторого короткого интервала времени усло­вие f_о = f_x строго выполняется и на экране наблюдается неподвижное изображение эллипса. Если затем частота f_x изменится, т.е. получит приращение  Df = = const (строго говоря, ни частота f_x, ни частота f_o никогда не являются постоянными), то разность фаз образцового и исследуемого напряжений будет изменяться прямо пропорционально времени. Покажем это.

Пусть образцовое напряжение  u₁ = U_m1 cos2πf_ot = U_m1 cosФ₁, а исследуемое напряжение  u₂ = U_m2 cos2πf_xt = U_m2 cos2π (f_o + Df ) t  =  U_m2 cosФ₂. Тогда разность фаз  Ф₂ – Ф₁ = = 2π Df t,  что и  приводит  к «вращению» эллипса. Например, если Δf = 2 Гц, то полный цикл (период) вращения эллипса будет равен 0,5 с.

При измерениях часто приходится производить отсчет измеряемой частоты при медленно «вращающемся» эллипсе и, тем самым, допускать погрешность сравнения, которая будет тем больше, чем быстрее «вращается» эллипс. Это одна составляющая результирующей погрешности измерения частоты методом интерференционных фигур.

Вторая составляющая результирующей погрешности измерения частоты этим методом – погрешность меры (погрешность частоты f_о образцового генератора).

Об измерении частоты методом интерференционных фигур см. также (1, с. 138 - 139).                                                                                                             

Приложение 7

Бланк отчета о выполнении лабораторной работы

Кафедра ТОР

Метрология и радиоизмерения

О Т Ч Е Т