Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение
Высшего профессионального образования
«Уральский Федеральный Университет им. Первого Президента России Б.Н.Ельцина»
Кафедра «Термообработки и физики металлов»
Отчет по лабораторной работе
По курсу: «Организация и математическое планирование металлофизического эксперимента»
Студент: Кириллова И.Н.
Группа МТ-390702
Преподаватель: Водолазский Ф.В
Екатеринбург 2012
|
N эксп. |
C |
Cr |
Ni |
Yэксп |
Yрасч |
отклонение |
отклонение в квадрате |
|
1 |
0,3874 |
1,0483 |
2,5529 |
0,6500 |
0,7262 |
-0,0762 |
0,0058 |
|
2 |
0,0727 |
0,7533 |
3,4460 |
1,9500 |
2,0338 |
-0,0838 |
0,0070 |
|
3 |
0,1614 |
3,0337 |
2,4178 |
1,4000 |
1,3504 |
0,0496 |
0,0025 |
|
4 |
0,3121 |
2,8993 |
3,5952 |
0,8500 |
0,9234 |
-0,0734 |
0,0054 |
|
5 |
0,1976 |
1,0351 |
2,3790 |
1,4500 |
1,4217 |
0,0283 |
0,0008 |
|
6 |
0,3709 |
0,9839 |
3,5681 |
1,1000 |
0,9027 |
0,1973 |
0,0389 |
|
7 |
0,3425 |
3,0738 |
2,2488 |
0,6500 |
0,6483 |
0,0017 |
0,0000 |
|
8 |
0,1268 |
2,9086 |
3,5900 |
1,6500 |
1,6179 |
0,0321 |
0,0010 |
|
9 |
0,2752 |
2,5212 |
2,0687 |
0,9500 |
0,9403 |
0,0097 |
0,0001 |
|
10 |
0,2886 |
2,2678 |
1,8119 |
0,9500 |
0,8893 |
0,0607 |
0,0037 |
|
11 |
0,1873 |
1,8439 |
2,8357 |
1,4000 |
1,4235 |
-0,0235 |
0,0006 |
|
12 |
0,2394 |
1,7757 |
0,7526 |
1,1500 |
1,0138 |
0,1362 |
0,0185 |
|
13 |
0,3719 |
1,9650 |
1,2719 |
0,3500 |
0,5514 |
-0,2014 |
0,0405 |
|
14 |
0,3297 |
1,4132 |
2,6759 |
0,9000 |
0,9172 |
-0,0172 |
0,0003 |
|
15 |
0,2023 |
1,2701 |
2,8944 |
1,4000 |
1,4340 |
-0,0340 |
0,0012 |
|
16 |
0,4299 |
1,1308 |
3,9508 |
0,7000 |
0,7061 |
-0,0061 |
0,0000 |
Среднее значение каждого элемента = СРЗНАЧ(В2:В17)
СКО = СТАНДОТКЛОН(B2:B17)
|
среднее |
0,2685 |
1,8702 |
2,6287 |
1,0938 |
|
ско |
0,1032 |
0,8190 |
0,8896 |
0,4238 |
Рассчитываем значения парных коэффициентов корреляции: = КОРРЕЛ(B2:B17;C2:C17), где В2:В17 и С2:С17 диапазоны каждой пары величин.
|
корреляция между |
Х1Х2 |
Х1Х3 |
Х2Х3 |
Х1Y |
X2Y |
X3Y |
|
коэффициент корреляции |
-0,1018 |
-0,0573 |
-0,1820 |
-0,9194 |
-0,1506 |
0,3130 |
Рассчитываем коэффициенты аi матричным методом, для этого составляем главную матрицу коэффициентов парной корреляции и находим её определитель =МОПРЕД(J2:L4). После нахождения определителя главной матрицы, составленной по коэффициентам r(xiy) составляем вспомогательные матрицы, столбцом значений r(xiy) поочередно заменяем каждый из столбцов главной матрицы, находим их определители.
|
главная матрица |
определитель |
|||
|
1,0000 |
-0,1018 |
-0,0573 |
||
|
-0,1018 |
1,0000 |
-0,1820 |
0,9511 |
|
|
-0,0573 |
-0,1820 |
1,0000 |
||
|
вспомогательная матрица 1 |
||||
|
-0,9194 |
-0,1018 |
-0,1018 |
||
|
-0,1506 |
1,0000 |
-0,1820 |
-0,8694 |
|
|
0,3130 |
-0,1820 |
1,0000 |
||
|
вспомогательная матрица 2 |
||||
|
1,0000 |
-0,9194 |
-0,0573 |
||
|
-0,1018 |
-0,1506 |
-0,1820 |
-0,1945 |
|
|
-0,0573 |
0,3130 |
1,0000 |
||
|
вспомогательная матрица 3 |
||||
|
1,0000 |
-0,1018 |
-0,9194 |
||
|
-0,1018 |
1,0000 |
-0,1506 |
0,2118 |
|
|
-0,0573 |
-0,1820 |
0,3130 |
||
Находим вспомогательные коэффициенты аi=M8/M3 рассчитаны как отношение определителя i-й матрицы к определителю главной матрицы.
|
а1 |
-0,9141 |
|
а2 |
-0,2045 |
|
а3 |
0,2227 |
Далее находим коэффициенты уравнения b1=P2*E19/B19, b2=P3*E19/C19, b3=P4*E19/D19, где Р2, Р3, Р4 — значения коэффициентов а1, а2, а3 соответственно, E19 — СКО значений ударной вязкости, B19, C19, D19 — СКО значений содержания С, Cr, Ni.
b0=E18-(S2*B18+S3*C18+S4*D18), E18 – среднее значение ударной вязкости, S2 – значение коэффициента b1, B18 — среднее значение содержания С, S3— значение коэффициента b2, C18 — среднее значение содержания Cr, S4 — значение коэффициента b3, D18 — среднее значение содержания Ni.
|
b1 |
-3,7551 |
|
b2 |
-0,1058 |
|
b3 |
0,1061 |
|
b0 |
2,0210 |
Сводный (общий) коэффициент корреляции R=КОРЕНЬ(P2*E23+P3*F23+P4*G23), где Р2— значение коэффициента а1, E23 — парный коэффициент корреляции между С и КСU, P3 – значение коэффициента а2 , F23 — парный коэффициент корреляции между Cr и KCU, P4 – значение коэффициента а3, G23 — парный коэффициент корреляции между Ni и KCU.
|
сводный коэффициент R |
0,9701 |
Далее рассчитываем KCU расч= $S$5+$S$2*B2+$S$3*C2+$S$4*D2, где S5 — значение b0, S2 — значение b1, B2 — значение содержания С, S3 — значение b2, C2 — значение содержания Cr, S4 — значение b3, D2 — значение содержания Ni.
Находим значение дисперсии неадекватности Sнеадекват=H18/(16-3-1).
Для оценки адекватности зависимости рассчитаем значения критерия Фишера расчетное и теоретическое: Fрасч= B25/E19, В25 — значение дисперсии неадекватности, Е19 — значение дисперсии KCU.
Fтеор=FРАСПОБР(0,95;16-3;16-1), где 0,95 — доверительная вероятность, 16 -3 и 16-1 число степеней свободы.
|
Sнеадекват |
0,0105 |
|
Fрасч |
0,0248 |
|
Fтеор |
0,3948 |
Fрасч<Fтеор — адекватная зависимость.
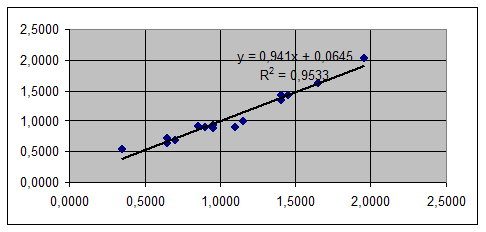
Полученная зависимость является линейной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.