Описание кристаллического многогранника. Сплошная кристаллическая среда. Элементы симметрии кристаллического многогранника. Анизотропия свойств кристалла, страница 2

·  имеет прямые углы, если это возможно, и равные длины ребер;

·  обладает наименьшей площадью.

10.  В выбранной Вами системе координат произведите индицирование: а) всех вершин кристалла; б) всех ребер кристалла; в) всех граней кристалла; г) всех направлений, идущих по диагоналям граней кристалла.

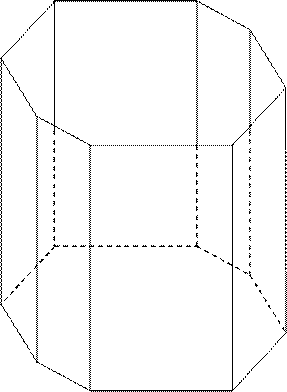
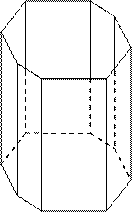
Обозначим оси координат, узлы и диагонали граней кристаллического многогранника (Рис. 6):

 

Рис. 6

а) Вершины кристалла:

                                                                       

                                                                       

                                                                      

                                                                  

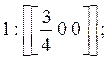
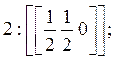
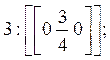
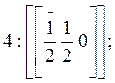
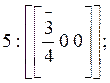
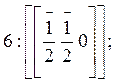
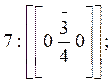
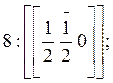
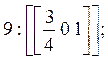
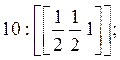
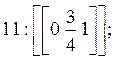
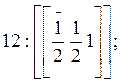
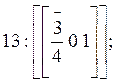
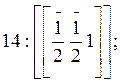
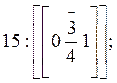
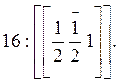
б) Ребра кристалла:

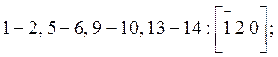
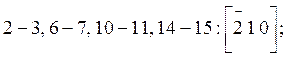
в) Грани кристалла:

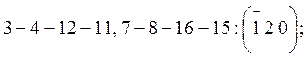
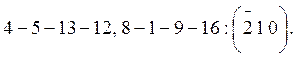
г) Диагонали граней кристалла:

                                        

                                      

                                       

                                        

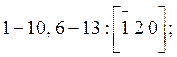
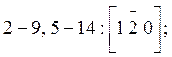
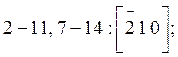
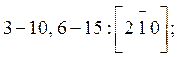
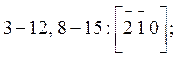
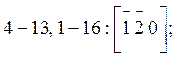
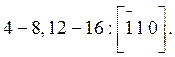
11.  Что такое семейство плоскостей кристалла? Найдите такие грани кристалла, которые относятся к одному семейству плоскостей. Определите индексы различных семейств плоскостей и количество плоскостей, входящих в семейство. Представьте для каждого  семейства рисунок.

Плоскость относится к семейству {hkl}, если при воздействии на нее элементами симметрии, присущими какому-либо классу, получается кристаллический многогранник, являющийся простой формой данного класса и состоящий из плоскостей данного семейства.

		а                                                      б                           Рис. 7

 

     К семейству {100} относятся грани  с индексом (001) (Рис. 7а).

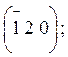
К семейству {120} относятся грани  с индексом (210);  с индексом (120);  с индексом   с индексом 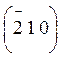 (Рис. 7б).

12.  Что такое зона в кристаллическом многограннике, что такое ось зоны? На рисунке покажите плоскости кристаллического многогранника, принадлежащие одной зоне, осью которой является направление: а) [001], б) [010], в) [100].

Кристаллографическая зона – серия плоскостей, параллельных какому либо направлению [uvw] в решетке. Данное направление называется осью зоны.

                                                                                                                                

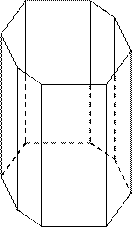
                       а                                                б                                                   в

Рис. 8

13.  Найдите все возможные значения углов между гранями кристаллического многогранника, согласно представленным формулам.

     Для тетрагональной сингонии формула имеет вид:

.

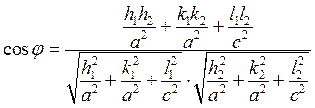Данный кристаллический многогранник имеет три различных угла между плоскостями:

·  угол между плоскостью (001) и любой из плоскостей семейства {120}

;

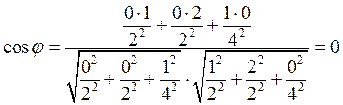·  угол между плоскостями (210) и (120)

;

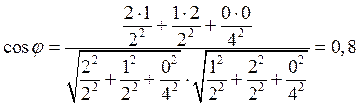·  угол между плоскостями (120) и :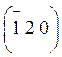

;

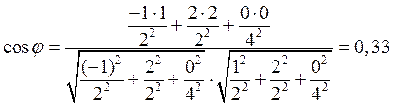14.  Рассчитайте объем элементарной ячейки кристаллического многогранника.

Объем заданного кристаллического многогранника можно рассчитать следующим образом:

.

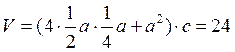15.  Произведите индицирование всех элементов симметрии кристаллического многогранника.

·  Плоскости симметрии (Рис. 2):

а) (001);       б1) (010);       б2) 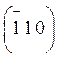;       б3) (100);       б4) (110).

·  Оси симметрии (Рис. 3):

а) [001];       б1) [100];       б2)[110];       б3) [010];       б4) .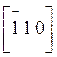

·  Центр симметрии (Рис. 4):

.

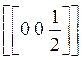16.  Построить стереографическую проекцию всех граней кристаллического многогранника.

 

Рис. 9

17.  Построить стереографическую проекцию всех элементов симметрии кристаллического многогранника.

 

Рис. 10

18.  Построить гномостереографическую проекцию всех граней кристаллического многогранника.

 

Рис. 11

19.  Что такое анизотропия свойств кристалла? Проявляется ли у Вашего кристаллического многогранника анизотропия свойств (физических, механических и т.д.)?

Анизотропия – неодинаковость свойств кристалла (например, упругости, электропроводности, теплопроводности, показателя преломления света и др.) по различным направлениям внутри этого кристалла.

У рассматриваемого кристаллического многогранника будет проявляться анизотропия свойств, так как он относится к среднему классу симметрии и «вытянут» вдоль направления [001].