Нормативная оценка надёжности и долговечности металлических мостов, страница 3

N=2×10⁶ – базовое число циклов.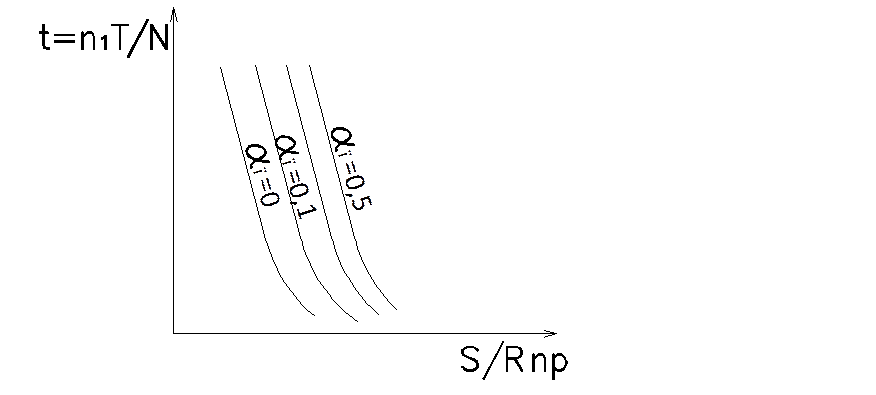

Полученные экспериментальные кривые могут быть аппроксимированы уравнением:

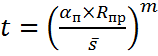           (A)

Требуемая долговечность  t  может быть реализована при приемлемой прочности бетона , величина которой является корнем уравнения (А), откуда может быть получено

.

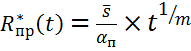Вследствие статистического характера прочности бетона  носит статистический характер. Очевидно, что отказ (разрушение) бетона наступает тогда, когда фактическая прочность меньше требуемой величины , т.е. отказ равен функции распределения .

 ,

а вероятность безотказной работы

  .

Прочность бетона достаточно хорошо описывается нормальным залогом распределения, поэтому приняв нормальный закон, можно написать:

   

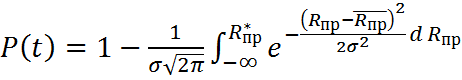
Здесь  – м.о.  бетона;

  - среднеквадратичное отклонение призменной прочности бетона.

Введём функцию Лапласа. Тогда искомая вероятность безотказной работы  может быть выражена в виде (см. раздел по нормальным распределениям):

 .

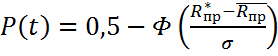Преобразуем аргумент формулы Лапласа, представив его в другом виде:

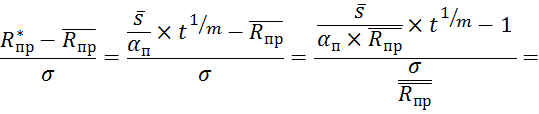
В этом выражении:

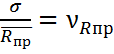– коэффициент вариации призменной прочности бетона;

Обозначим 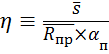 . После этого

 .

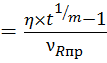Т.о.

 (**).

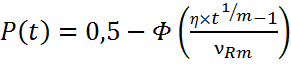По этой формуле, в зависимости от прочности бетона и его качества (описывает коэффициент вариации  и параметром ) и величины нагружённости (параметр ) для данного t (связанного с заданным сроком службы T формулой   можно найти вероятность безотказной работы. Надо иметь просто таблицы функций Лапласа.

Помимо знания вероятности безотказной работы  при заданном сроке службы может потребоваться знание срока службы Т при заданной вероятности безотказной работы . Другими словами, найти также значение t, при котором вероятность  имеет заранее заданное значение, т.е. необходимо найти квантиль t, соответствующей вероятности . Как это сделать?

Мы имеем:

 .

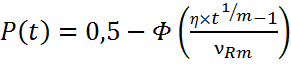Пусть γ – такое значения аргумента функции Лапласа , при котором вероятность  приобретает требуемое значение, т.е.

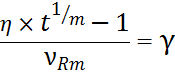
откуда

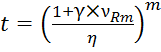
Т.к.  , то

,

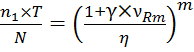откуда .

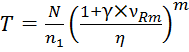Величину  можно найти, используя таблицы функции Лапласа. Методика расчёта понятна из примеров расчёта.

Задаваемая вероятность безотказной работы	0,550%	0,990%	0,998%	0,9999%	0,99999,9%
	0	-0,4	-0,48	-0,49	0,499
- по таблицам функции	0	-1,282	-2,054	-2,326	-3,090

Оценка ресурса ж.б. элементов по выносливости арматуры

Гипотеза линейного суммирования  усталостных повреждений, широко применяемая для расчёта металлических конструкций, оказывается справедливой, как показывают экспериментальные данные, и для арматуры ж.б.м., если напряжения в них не очень велики, т.е. условия прочности выполняются, и разрушение наступает вследствие исчерпания ресурса по выносливости.

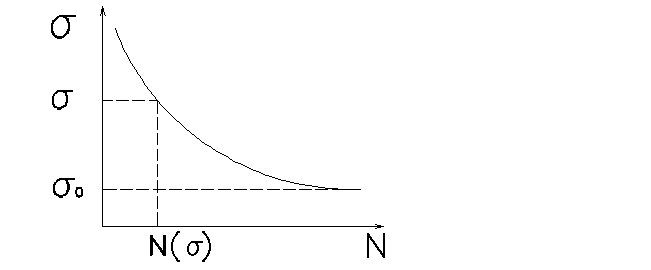
Кривая выносливости арматуры N(σ) зависит от вида арматуры, концентрации напряжений, относительной величины (доли) напряжений от постоянной нагрузки (характеризует ρ –характеристику цикла), условий работы арматуры в теле бетона:

 σ₀ – напряжения, ниже которых усталостные повреждения в металле не накапливаются.

Пусть для некоторого максимального напряжения в цикле σ число циклов по кривой усталости N(σ). Тогда мера повреждения от действия одного цикла напряжений .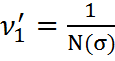

Действующие напряжения σ – изменяются статистически. Значение σ может быть с вероятностью P(σ),т.е. 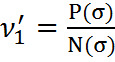  . Для определения повреждения от одного цикла с учётом статистического характера действующих напряжений надо интегрировать выражение   по всему диапазону возможных изменений σ, вызывающих усталостные повреждения, т.е.

.

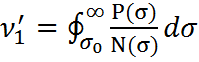Если n₁ – число циклов загружения в год, а Т – срок службы, то по теории линейного накопления усталостных повреждений:

 ,

откуда

.

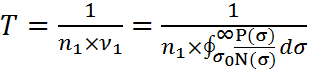Полученное выражение позволяет вычислить ресурс ж.б. по выносливости арматуры, если известны кривая выносливости и закон распределения напряжений в арматуре .

Для практического пользования более удобным представляется такая методика, которая бы была аналогична методике оценки усталостного ресурса для бетона. В пользу этого говорит тот факт, что экспериментальные результаты как для бетона, так и для арматуры, получаются в одних тех же экспериментах, т.к. на работу бетона оказывает огромное влияние арматура, и наоборот. Поэтому для арматуры, как и для бетона, были получены кривые зависимости ресурса t от статической прочности σ_вр арматуры, доли напряжений от постоянной нагрузки, и от полной нагрузки.

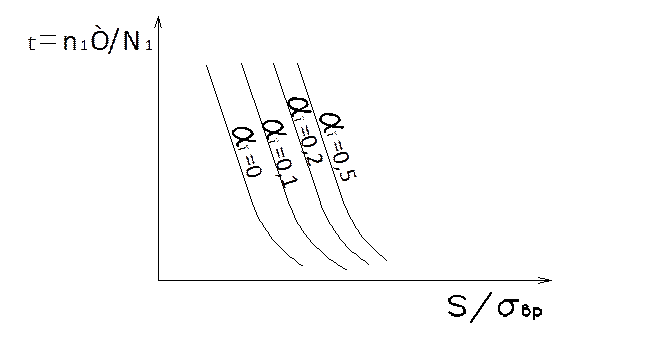
Эти кривые, так же, как и для бетона, могут быть выражены уравнением:

.

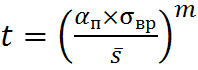Поэтому, все формулы, полученные для бетона, справедливы и для арматуры, с заменой только характеристик работы и прочности бетона на характеристики работы и прочности арматуры.