Изучение молекулярных спектров поглощения при помощи фотометра ФМ-58 (лабораторная работа), страница 3

, т.е.

                                                     .                                                (1.6)

Из формулы (1.6) следует, что расстояния между соседними вращательными уровнями увеличиваются с ростом квантового числа у. Таким образом, полную энергию молекулы можно представить как сумму:

                                                                                                    (1.7)

или, учитывая (1.1) и (1.5)

.

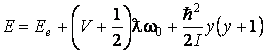В основном состоянии все три вида энергии имеют минимальные величины. Теория и опыт показывают, что наибольшие значения принимают разности электронных энергий, а наименьшие – :

 эВ;  эВ;  эВ, т.е.

                                                      .                                           (1.8)

Таким образом. Каждый электронный уровень расщепляется на колебательные подуровни, расположенные на одинаковом «расстоянии»  друг от друга (формула 1.4). Каждый колебательный уровень распадается на вращательные подуровни, расстояния между которыми определяются формулой 1.6. Схема энергетических уровней двухатомной молекулы приведена на рисунке 1.2.

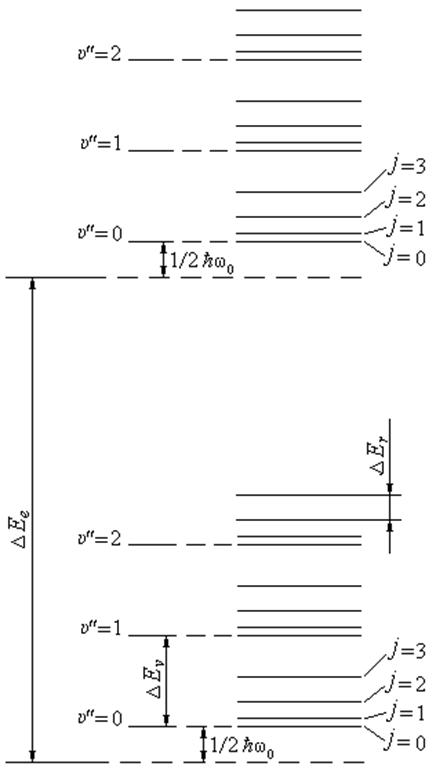
Рисунок 1.2. – Схема энергетических уровней молекулы

При сообщении молекуле достаточного количества энергии, она переходит в возбужденное состояние и затем, совершая переход в одно из более низких энергетических состояний, излучая квант энергии

                                                      .                                   (1.9)

Частота излучения, испускаемого при изменении состояния молекулы, определяется так:

                                                 .                                      (1.10)

          В зависимости от того, изменение каких видов энергии (вращательной, колебательной, электронной) обусловливает испускание молекулой фотона, различают три вида полос в спектре молекулы:

1.  вращательное;

2.  колебательно - вращательные;

3.  электронно-колебательные.

Линии чисто вращательного спектра лежат в далекой инфракрасной или микроволновой областях спектра. Они возникают при переходах молекулы из одного вращательного состояния в другое (электронная конфигурация молекулы и ее колебательная энергия при этом не изменяются).

          Возможные изменения квантового числа у ограничиваются правилом отбора , т.е. переходы совершаются между соседними вращательными уровнями. Частоты квантов, испускаемых при переходах между вращательными уровнями определятся из формул (1.6) и (1.10):

                                                                                            (1.11)

или                                                        ,                                          (1.12)

где .

Вращательный спектр (рисунок 1.3) состоит из системы равноотстоящих линий. Расстояние между линиями определяется из формулы (1.12):