Определение расчетных гидрологических характеристик: Методические указания к лабораторным работам, страница 7

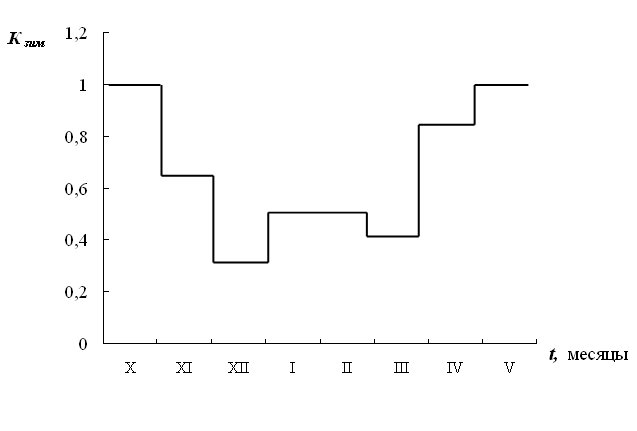
Рис. 5.  Изменение коэффициента зимнего уменьшения расхода воды

Снижение значений расхода воды в зимний период вызвано наличием ледовых явлений на реке (льда, шуги и т.п.).

ЛАБОРАТОРНАЯ РАБОТА  3

ПОСТРОЕНИЕ КРИВОЙ ОБЕСПЕЧЕННОСТИ МАКСИМАЛЬНЫХ РАСХОДОВ ВОДЫ  ПРИ НАЛИЧИИ МНОГОЛЕТНИХ ДАННЫХ

ГИДРОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ

Вводные понятия

Сток реки подвержен непрерывным колебаниям, на которые оказывают влияние многочисленные климатические, физико-географические и антропогенные факторы. Поэтому применяемый метод прогноза характеристик стока основан на обобщении методами теории вероятностей результатов гидрометрических наблюдений за длительный период времени. Продолжительность периода наблюдений считается достаточной, если величина относительной среднеквадратической ошибки не превышает 10 %.

Определение расчетных гидрологических характеристик осуществляется путем применения функций распределения ежегодных вероятностей превышения (называемых также кривыми обеспеченности). Кривая распределения ежегодных вероятностей превышения максимальных расходов воды является объективной характеристикой реки и показывает число случаев за расчетный период (в процентах), когда максимальный годовой расход будет не менее любого заданного значения; при этом предполагается, что основные факторы стока в будущем останутся неизменными.

Исходными данными являются результаты многолетних наблюдений за ежегодными максимальными расходами воды в водотоке.

Прядок выполнения работы

1. Построение эмпирической кривой распределения. В табл. 7 вписывают измеренные значения максимальных расходов воды в водотоке в хронологическом порядке. Далее строят ранжированный ряд, т.е. значения расходов воды записывают в убывающем порядке. В  табл. 7 также записывают порядковые номера ранжированного ряда.

Далее определяют эмпирическую ежегодную вероятность превышения  (обеспеченность) максимальных расходов, которая вычисляется для каждого члена ранжированного ряда, по формуле

                                                            (2)

где m – порядковый номер члена ранжированного ряда; n – общее количество членов ряда, равное числу наблюдений.

Вычисленные значения заносят в табл. 7. Далее определяют среднее значение максимального расхода Q_о, а также – для каждой строки – модульный коэффициент  К_m по формулам

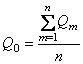      и .                                           (3)

При этом для столбцов 5 и 6 табл. 7 должен выполняться контроль:

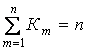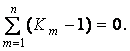      и                                           (4)

Если итог суммирования (с точностью до второго знака после запятой) отличается от требуемого (4), разница распределяется между слагаемыми. Только после этого вычисляют данные следующих столбцов таблицы. Далее строят эмпирическую кривую обеспеченности максимальных расходов воды, представляющую собой зависимость модульных коэффициентов К_m от обеспеченности  р.  Для построения графика используется полулогарифмическая сетка.

Эмпирическая кривая  обладает двумя  существенными недостатками. Во-первых, она имеет вид ломаной, т. е. не охватывает непрерывного ряда значений, которые может принять случайная величина расхода. Во-вторых, она не определена в зонах значений наименьших и наибольших вероятностей превышения (р<3,8% и р>96,2%), особо необходимых для гидрологических расчетов. Устранить эти недостатки позволяет аналитическая кривая. Для сглаживания и экстраполяции эмпирических кривых обеспеченности используются, как правило, трехпараметрическое гамма-распределение (распределение С.М. Крицкого – М.Ф. Менкеля) и биномиальное распределение. В соответствии с СП 33-01-2003 биномиальное распределение допускается применять только при соответствующем технико-экономическом обосновании.