Разработка влагомера для блока отображения информации бортового радиолокационного комплекса, страница 3

Реальный элемент при расчете на прочность заменяется математической моделью, вид которой зависит от типа радиоэлемента и способа его крепления.  В качестве расчетной модели навесного элемента, закрепленного на выводах, принимают прямоугольную раму с защемленными краями и сосредоточенной массой (рис. 5).

                        

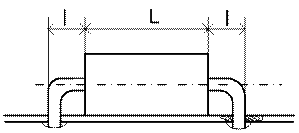
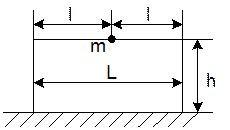
Рис. 5а.   Реальный элемент                     Рис. 5б. Математическая модель

3.2.РАСЧЕТ НА ДИНАМИЧЕСКУЮ ПРОЧНОСТЬ ВЫВОДОВ НАВЕСНОГО ЭЛЕМЕНТА

Реальный элемент, а именно резистор С5-5 с параметрами:

L = 20 мм

D =6,15 мм

h =6 мм

d = 1 мм

Выводы выполнены из медной проволоки, для которой σ_в=400 МПа, σ_-1=100 МПа, Е=1,23*10⁵ МПа (1,23*10¹¹ Н/м²)

Определяем собственную частоту колебаний математической модели.

Для математической модели в виде упругой рамы в случае действия силы перпендикулярно оси навесного элемента и плоскости печатной платы, формула для расчета собственной частоты колебаний  f₀ будет иметь вид:

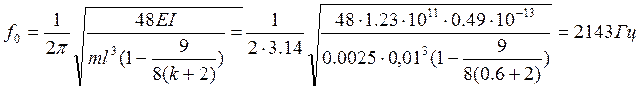, где

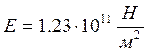 - модуль упругости первого рода материала выводов;

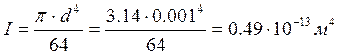 - осевой момент инерции поперечного сечения вывода;

d – диаметр вывода, м;

  - длина вывода от точки изгиба до радиоэлемента;

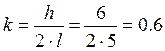
 Определяем частотное отношение по формуле:

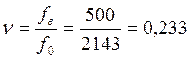
В дорезонансной зоне, когда , инерционная сила P_и, действующая на элемент, определяется как:

Где  g – ускорение свободного падения;

= 15 –вибрационная перегрузка.

 Определяем изгибающие моменты в точках расчетной модели, где их значение наибольшее. Для данного случая изгибающие моменты максимальны в точках А и D и определяются по формуле:

 

В этих точках изгибающие моменты создают напряжения:

а) изгибающие напряжения, определяемые по формуле:

,

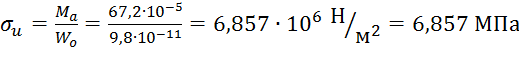где 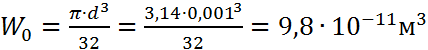 - осевой момент сопротивления поперечного сечения вывода;

 - площадь поперечного сечения вывода.

Эквивалентное напряжение в сечении при действии указанных напряжений определяется как:

  

 

Согласно условию прочности эквивалентное напряжение не должно превышать величины допускаемого напряжения для материала

.

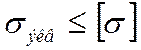Допускаемое напряжение в условиях действия знакопеременных нагрузок рассчитаем из выражения:

 ,

Где  - предел усталости – предельное напряжение, которое может выдержать испытуемый образец без разрушения за заданное количество циклов колебаний;

n- коэффициент запаса прочности, равный 1,8…2;

- эффективный коэффициент концентрации напряжений, равный 1.0…1.2

Условие прочности: ; .

Условие выполняется, поэтому указанный способ крепления резистора соответствует характеру и величине приложенных усилий.

3.3 РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ ВЫВОДОВ НАВЕСНОГО ЭЛЕМЕНТА

Предполагается, что на элемент одновременно воздействуют линейные, ударные и вибрационные нагрузки, тогда инерционная сила, приложенная к элементу, составит:

, где

n_л = 10– линейная перегрузка;

n_уд = 25 – ударная перегрузка;

n_в = 15 – вибрационная перегрузка.

Для полученного значения инерционной силы, ведем расчет, аналогичный расчету на динамическую прочность выводов навесного элемента.

Определяем изгибающие моменты в точках расчетной модели, где их значение наибольшее. Для данного случая изгибающие моменты максимальны в точках В и С и определяются по формуле:

 

В этих точках изгибающие моменты создают напряжения:

а) изгибающие напряжения, определяемые по формуле:

,

 

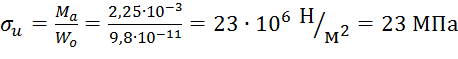Эквивалентное напряжение в сечении при действии указанных напряжений определяется как:

.

Согласно условию прочности эквивалентное напряжение не должно превышать величины допускаемого напряжения для материала:

.

Из условия статической прочности допускаемое напряжение равно:

 , где

- предел прочности материала вывода элемента;

n- коэффициент запаса прочности, равный 3…5;

Условие прочности выполняется, т.к :