Реферат
Пояснительная записка содержит 26 страниц, 12 рисунков, 1 таблица, список литературы из 10 наименований.
Цель данного курсового проекта – является создание программного продукта «Решение задачи использования мощностей оборудования графическим методом».
В первом разделе курсового проекта осуществляется постановка задачи прогнозирования и приводится анализ алгоритма решения задачи.
Во втором и в третьем разделе – производится выбор аппаратных и инструментальных средств для реализации поставленной задачи.
В четвертом разделе приведено описание разрабатываемого программного приложения, рассмотрен листинг программного продукта, блок – схема алгоритма работы программы.
В пятом разделе рассматриваются вопросы аналитического и программного решения задачи, проводится сравнительный анализ получившихся результатов.
В заключительном разделе пояснительной записки сделаны выводы о проделанной работе, рассмотрены достоинства разработанного продукта, его перспективы развития.
Введение
Линейное программирование - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать. Графический метод, несмотря на свою очевидность и применимость лишь в случае малой размерности задачи, позволяет понять качественные особенности задачи линейного программирования, характерные для любой размерности пространства переменных и лежащие в основе численных методов ее решения.[1] Целью курсового проекта является создание программного продукта «Решение задачи использования мощностей оборудования графическим методом». Программный продукт представляет собой форму на которой расположены поля для ввода и вывода, таблица которую заполняют значениями переменных, график, отображающий данные и целевую функцию.
Усложнение производства, техники и организационной структуры общества приводит к тому, необходимо составлять программы для решения задач линейного программирования графическим методом, которые значительно сокращают трудоемкость и время работы. Поэтому данный программный продукт является актуальным при решении задач линейного программирования графическим методом.
Новизной данной разработки является использование современных технологий при решении задач линейного программирования графическим методом, позволяющие ускорить быстродействие решения задач. Современные элементы программирования интерфейса делают его для пользователя интуитивно понятным, а сама программа удобна в использовании.
Областью применения программного продукта могут быть различные предприятия и службы, заинтересованные в информации такого рода.
1 Постановка задачи моделирования
1.1 Описание задачи моделирования
Задачи оптимального планирования связаны с окончанием оптимума заданной целевой функции (линейной формы) при наличии ограничений в виде линейных уравнений или линейных неравенств относятся к задачам линейного программирования.[3]
1. Математические модели очень многих задач линейны относительно искомых переменных.
2. Эти задачи наиболее изучены.
3. Многие задачи ЛП, будучи решенными, используются на практике.
4. Некоторые задачи, которые в первоначальной форме не являются линейными, после ряда дополнительных ограничений становятся линейными.[2]
Графический
метод решения задач ЛП.Используется для задач с двумя переменными.
Каждое из неравенств ограничений определяет некоторую полуплоскость. Система
неравенств в целом – пересечение полуплоскостей. ОДР всегда представляет собой
выпуклую фигуру. ОДР графически может быть представлена выпуклым многоугольником,
неограниченно выпуклой многоугольной областью, отрезком, лучом, одной точкой.
Целевая функция ![]() при фиксированном значении
при фиксированном значении ![]() определяет
на плоскости прямую линию
определяет
на плоскости прямую линию ![]() . Изменяя значения L, мы получим семейство
параллельных прямых, называемых линиями уровня. Это связано с тем, что
изменение значения L повлечет лишь изменение длины отрезка, отсекаемого
линией уровня оси X2,
а угловой коэффициент
. Изменяя значения L, мы получим семейство
параллельных прямых, называемых линиями уровня. Это связано с тем, что
изменение значения L повлечет лишь изменение длины отрезка, отсекаемого
линией уровня оси X2,
а угловой коэффициент 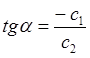 останется неизменным. Поэтому для решения
достаточно построить одну из линий уровня, произвольно выбрав значение L.
останется неизменным. Поэтому для решения
достаточно построить одну из линий уровня, произвольно выбрав значение L. ![]() перпендикулярен
каждой из линий уровня. Направление вектора совпадает с направлением
возрастания целевой функции. Направление убывания целевой функции
противоположно направлению
перпендикулярен
каждой из линий уровня. Направление вектора совпадает с направлением
возрастания целевой функции. Направление убывания целевой функции
противоположно направлению ![]() . Суть метода: по направлению (против) вектора
. Суть метода: по направлению (против) вектора ![]() в ОДР
производится поиск оптимальной точки
в ОДР
производится поиск оптимальной точки ![]() . Оптимальной считается точка, через которую
проходит линия уровня
. Оптимальной считается точка, через которую
проходит линия уровня ![]() , соответствующая значению функции
, соответствующая значению функции ![]() . Оно всегда находится на границе ОДР: в вершине
многоугольника или на всей его стороне.[2],[5]
. Оно всегда находится на границе ОДР: в вершине
многоугольника или на всей его стороне.[2],[5]
1.2 Алгоритм решения задачи
Предприятие
имеет две модели машин различных мощностей. Задан план по времени и
номенклатуре: Т — время работы каждой машины; продукции -го вида должно
быть выпущено не менее ![]() единиц. Необходимо составить такой
план работы оборудования, чтобы обеспечить минимальные затраты на производство,
если известны производительность каждой -й машины по выпуску
единиц. Необходимо составить такой
план работы оборудования, чтобы обеспечить минимальные затраты на производство,
если известны производительность каждой -й машины по выпуску ![]() -го
вида продукции bij и стоимость единицы времени,
затрачиваемого
-го
вида продукции bij и стоимость единицы времени,
затрачиваемого ![]() -й
машиной на выпуск
-й
машиной на выпуск ![]() -го
вида продукции
-го
вида продукции ![]() .[2],[8]
.[2],[8]
1. Построим систему неравенств.
2. В ограничениях задачи все знаки неравенств заменяем на знаки равенств и строим соответствующие прямые.
3. Находим и заштриховываем каждую из разрешенных полуплоскостей.
4. Определяем ОДР. При отсутствии ОДР задача не имеет решений.
5. Если ОДР – непустое множество, строим целевую прямую, т. е. любую из линий уровня, где L – любое число, удобное для расчетов.
6. Построим вектор ![]() ,
который начинается в (0, 0) и заканчивается в
,
который начинается в (0, 0) и заканчивается в ![]() (целевая
функция и
(целевая
функция и ![]() перпендикулярны).
перпендикулярны).
7. Передвигаем целевую функцию в направлении (против
направления) вектора ![]() . Последняя по ходу движения
вершина ОДР будет искомой точкой. Целевая функция может быть не ограничена на
множестве.
. Последняя по ходу движения
вершина ОДР будет искомой точкой. Целевая функция может быть не ограничена на
множестве.
8. Определим координаты ![]() и
посчитаем значение
и
посчитаем значение ![]() (для вычисления координат
оптимальной точки
(для вычисления координат
оптимальной точки ![]() решим систему уравнений прямых,
на пересечении которых находится
решим систему уравнений прямых,
на пересечении которых находится ![]() ).[5],[2]
).[5],[2]
2 Выбор инструментальных средств, для реализации задачи
Для эффективности реализации задачи курсового проекта, необходимо
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.