Синтез комбинационных схем на универсальных элементах

Министерство общего и профессионального образования

Российской Федерации

Государственный Университет Аэрокосмического Приборостроения

Отчет защищен:

Преподаватель:

ОТЧЕТ

о лабораторной работе №21

по курсу «Теория автоматов»

Синтез комбинационных схем на универсальных

элементах

Работу выполнил

студент группы 4741                                                      /Миронов С.В./

Санкт-Петербург, 1998

Лабораторная работа №21

Синтез комбинационных схем на универсальных элементах

     Цель работы: изучение методов синтеза комбинационных схем и построение функциональных схем на универсальных логических элементах.

     Исходные данные: задана переключательная функция, см. Табл. 1.

Табл. 1

Заданная переключательная функция

ABCD	0000	0001	0010	0011	0100	0101	0110	0111
F	1	0	1	1	0	0	0	1

ABCD	1000	1001	1010	1011	1100	1101	1110	1111
F	0	1	0	1	1	0	0	0

1. Представить переключательную функцию диаграммой Вейча. Функция имеет n=4 аргументов, следовательно, диаграмма Вейча должна иметь 2⁴=16 клеток. Число n -четное, следовательно сторона таблицы будет равна  клеткам. Диаграмма приведена на Рис. 1.

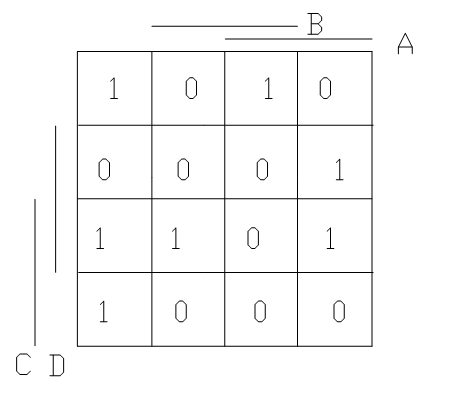
Диаграмма Вейча

Рис. 1

2. Минимизировать функцию с помощью диаграммы Вейча по 1 и 0. Выбрать минимальное представление. Используя метод, изложенный в методическом указании, покроем единичные клетки диаграммы Вейча прямоугольниками максимальных размеров со сторонами 2ⁱx2^j, где i, j -целые числа. Каждому полученному прямоугольнику ставится в соответствие некоторая кон’юнкция, в которой отсутствуют переменные, изменяющие в данном прямоугольнике свои значения. То же самое следует проделать с 0-выми клетками. Полученная диаграмма представлена на Рис. 2.

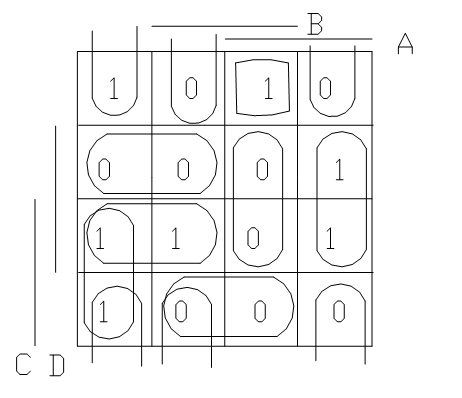
Диаграмма Вейча, заполненная методом

прямоугольников

Рис. 2

Получаемые формулы:

                                (1)

                                 (2)

     Для реализации (1) необходим 21 вход (16 на кон’юнкторы и 5 на диз’юнкторы), для реализации (2) необходимо 20 входов (15 на кон’юнкторы и 5 на диз’юнкторы). Следовательно, в данном случае выражение для обратного значения является более простым. Перейдем от обратного значения функции к кон’юнктивной форме представления прямого значения функции. Имеем:

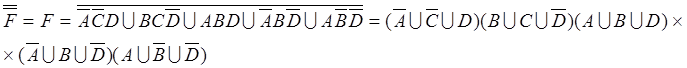     (3)

3. Перевод полученного выражения в универсальные базисы И-НЕ и ИЛИ-НЕ.

Переход к базису И-НЕ

Используя следующие формулы:

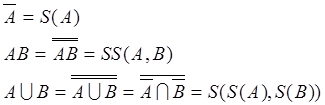                                 (4)

перейдем к базису И-НЕ. Имеем:

               (5)

     Переход к базису ИЛИ-НЕ

Используя следующие формулы:

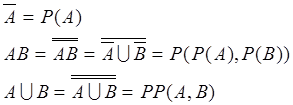                                    (6)

перейдем к базису ИЛИ-НЕ.

Имеем:

                (7)

4. Составление функциональной схемы.

Функциональную схему на элементах S и P см. На Рис. 3 и Рис. 4 соответственно.

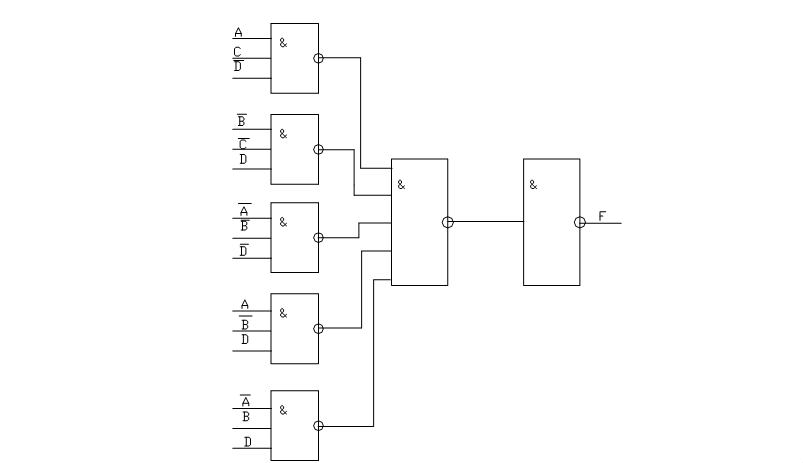
Функциональная схема на S -элементах

Рис. 3

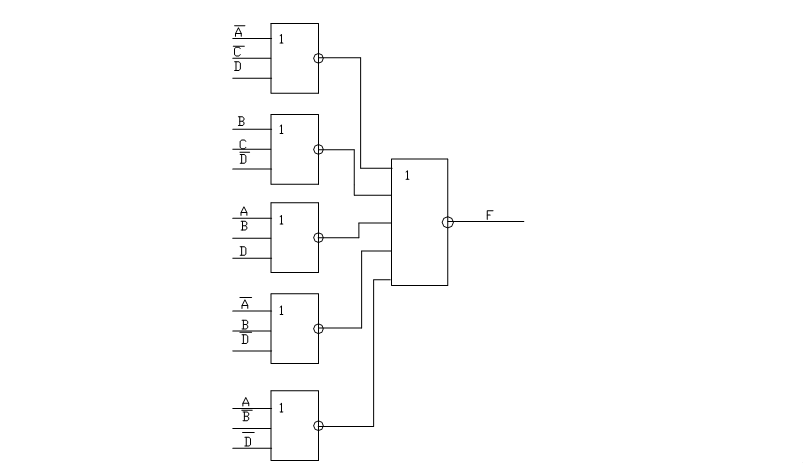
Функциональная схема на P -элементах

Рис. 4