














































цифру (от 0 до 9) представляют четырехразрядной двоичной тетрадой. Например:
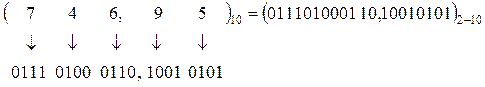 .
.
При обратном переводе двоично- десятичное число влево и вправо от запятой разбивают на четвертки цифр- тетрады, а затем каждую тетраду заменяют соответствующей десятичной цифрой. Например:
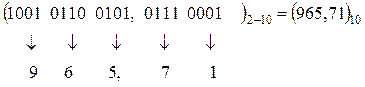 .
.
В табл. 2.1 приведены записи чисел от 0 до 20 в различных системах счисления.
Таблица 2.1.
Представление чисел в различных системах счисления
|
10- чная |
2- чная |
8- чная |
16- чная |
2-10- чная |
|
0 |
0 |
0 |
0 |
0000 |
|
1 |
1 |
1 |
1 |
0001 |
|
2 |
10 |
2 |
2 |
0010 |
|
3 |
11 |
3 |
3 |
0011 |
|
4 |
100 |
4 |
4 |
0100 |
|
5 |
101 |
5 |
5 |
0101 |
|
6 |
110 |
6 |
6 |
0110 |
|
7 |
111 |
7 |
7 |
0111 |
|
8 |
1000 |
10 |
8 |
1000 |
|
9 |
1001 |
11 |
9 |
1001 |
|
10 |
1010 |
12 |
А |
00010000 |
|
11 |
1011 |
13 |
В |
00010001 |
|
12 |
1100 |
14 |
С |
00010010 |
|
13 |
1101 |
15 |
D |
00010011 |
|
14 |
1110 |
16 |
E |
00010100 |
|
15 |
1111 |
17 |
F |
00010101 |
|
16 |
10000 |
20 |
10 |
00010110 |
|
17 |
10001 |
21 |
11 |
00010111 |
|
18 |
10010 |
22 |
12 |
00011000 |
|
19 |
10011 |
23 |
13 |
00011001 |
|
20 |
10100 |
24 |
14 |
00100000 |
Перевод из одной системы счисления в другую
Рассмотрим общие правила перевода чисел из одной позиционной системы счисления в другую.
1. Перевод целого числа из системы счисления с основанием S в другую систему с основанием Q осуществляется последовательным делением его на основание Q новой системы счисления до тех пор, пока не получится частное, меньшее Q. Число в новой системе запишется в виде остатков деления, начиная с последнего. Указанное деление выполняется в исходной системе счисления.
Выполним по этому правилу перевод десятичного числа 377(10) сначала в двоичную, а затем в восьмеричную и шестнадцатеричную системы.
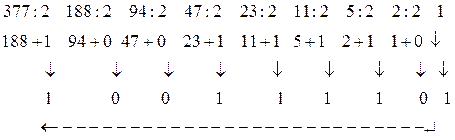
Аналогично выполним перевод в восьмеричную и шестнадцатеричную системы счисления:
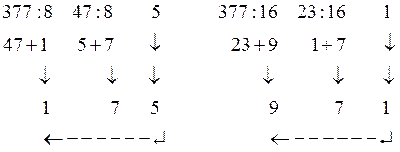
Остатки от соответствующих делений дают записи в новых системах счисления, т.е. 377(10) = 101111001(2) = 571(8) = 179(16).
2. Перевод правильной дроби из одной позиционной системы счисления в другую осуществляется последовательным умножением ее на основание новой системы счисления; при этом перемножаются только дробные части. Дробь в новой системе счисления записывается в виде целых частей получающихся произведений, начиная с первого.
Например, переведем десятичную дробь 0,6875 в двоичную, восьмеричную и шестнадцатеричную системы счисления:
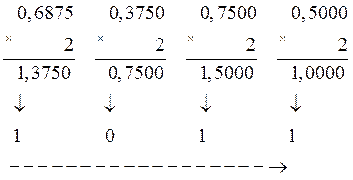 ,
,
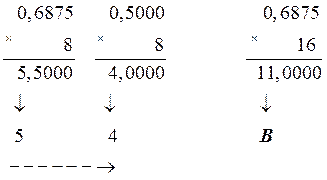 .
.
В шестнадцатеричной системе счисления целая часть произведения 11 запишется символом В (см. табл. 2.1), поэтому окончательно получим 0,6875(10) = 0,1011(2) = 0,54(8) = 0,В(16).
При переводе дробей в новую позиционную систему счисления последовательное умножение на основание этой системы выполняют до получения дробной части, равной нулю или до получения необходимого количества разрядов после запятой.
3. Для перевода неправильных десятичных дробей в новую позиционную систему счисления (например, 15,6875) необходимо, пользуясь приведенными правилами, выполнить отдельно перевод целой и дробной частей.
4. Обратный перевод в десятичную систему счисления из других позиционных систем счисления выполняется с использованием позиционного разложения в степенной ряд исходного числа. Для этого данное число представляется в виде суммы степеней своего основания, вычисляются значения десятичных эквивалентов отдельных разрядов, которые затем суммируются. Например:
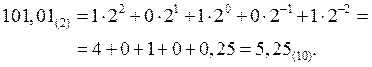
![]()
![]()
Двоичная арифметика
Особенностью двоичной системы счисления является то, что арифметические операции в ней очень просты. Для выполнения четырех арифметических действий используются обычные правила арифметики.
Сложение двоичных чисел. Приведем правила сложения двоичных чисел: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10. Пользуясь этим правилом, можно выполнять сложение многоразрядных двоичных чисел подобно тому, как это делается в десятичной системе счисления. Необходимо только учитывать, что 1 + 1 дают 0 в данном разряде и 1 переноса в старший разряд. Сложим, например, по общему правилу двоичные числа 1100 (двенадцать) и 110 (шесть):
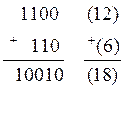 .
.
Проверим результат:
![]()
Более сложно выполняется сложение одновременно трех двоичных чисел и более. В этом случае нужно внимательно следить за образующимися единицами переноса в старшие разряды, поскольку эти единицы переноса могут переходить не только в соседние старшие разряды, но и в более удаленные.
Вычитание двоичных чисел. Приведем правила вычитания двоичных чисел: 0 – 0 = 0, 1 – 1 = 0, 1 – 0 = 1, 10 – 1 = 1. При вычитании многоразрядных двоичных чисел может возникнуть необходимость заема единицы в ближайшем старшем разряде, что дает две единицы младшего разряда. Если в соседних старших разрядах стоят нули, то приходится занимать единицу через несколько разрядов. При этом единица, занятая в ближайшем старшем разряде, дает две единицы в младшем разряде и единицы во всех нулевых разрядах, стоящих между младшим и тем старшим разрядом, у которого брался заем. например:
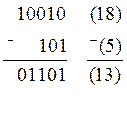 .
.
Проверим результат:
![]()
Умножение двоичных чисел. Приведем правила умножения двоичных чисел: 0 · 0 = 0, 0 · 1 = 0, 1 · 0 = 0, 1 · 1 = 1. Умножение двоичных чисел производят по тем же правилам, что и для десятичных чисел. При этом используют таблицу умножения и сложения. Умножение многоразрядных двоичных чисел сводится к умножению множимого на каждый разряд множителя, последующему сдвигу множимого или множителя и суммированию получающихся частичных произведений. Например:
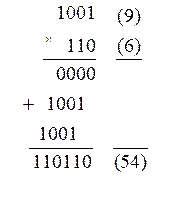 .
.
Проверим результат:
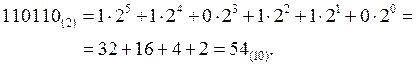 .
.
Деление двоичных чисел. При делении двоичных чисел используют таблицу умножения и вычитания. Правила деления аналогичны делению в десятичной системе и сводятся к выполнению умножений, вычитаний и сдвигов. Например, выполним деление 110110 (54) на 110 (6):
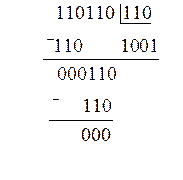 .
.
Проверим результат:
![]()
Логическая арифметика
Над информацией в ЭВМ производятся не только арифметические операции, но логические. Основные логические операции приведены в лабораторной работе № 1. Перед выполнением операции сначала необходимо выровнять порядки операндов, а затем уже производится сама логическая операция поразрядно.
Например, найдем инверсию двоичного числа 110100. Для этого заменяем все единицы на нули, а нули- на единицы. Получим новое двоичное число 001011.
Найдем конъюнкцию и дизъюнкцию двух двоичных чисел 1111 и 100:
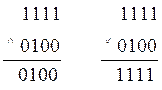 .
.
Сложение по модулю два (исключающее или) этих же двоичных чисел приводит к следующему результату:
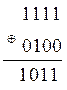 .
.
Лабораторное задание:
1. Машинная арифметика
1.1. Заданы два целых числа А(10) и В(10) (в десятичной системе счисления). Представить заданные числа в:
· двоичной,
· восьмеричной,
· шестнадцатеричной,
· двоично- десятичной
системах счисления. Произвести обратный перевод в десятичную систему счисления. Числа А(10) и В(10) выбрать из таблицы 2.2 в соответствии с вариантом.
1.2. Заданы две правильные дроби С(10) и D(10) (в десятичной системе счисления). Представить заданные числа в:
· двоичной,
· восьмеричной,
· шестнадцатеричной
системах счисления. Произвести обратный перевод в десятичную систему счисления. Числа С(10) и D(10) выбрать из таблицы 2.2 в соответствии с вариантом.
1.3. Над числами А(2) и В(2) (из п.п.1.1), представленных в двоичной системе счисления, произвести арифметические операции:
· сложения,
· умножения.
Произвести проверку полученных результатов с помощью арифметических операций:
· вычитания,
· деления.
2. Логическая арифметика
2.1. Над числами А(2) и В(2) (из п.п.1.1), представленных в двоичной системе счисления, произвести логические операции:
· конъюнкцию,
· дизъюнкцию,
· сложение по модулю два,
· отрицание.
2.2. Вычислить значение функции f(A,
B) = ![]() .
.
Индивидуальные варианты к лабораторнойработе
|
№ варианта |
А |
В |
С |
D |
|
1 |
125 |
37 |
0,25 |
0,125 |
|
2 |
130 |
40 |
0,27 |
0,135 |
|
3 |
135 |
43 |
0,30 |
0,145 |
|
4 |
145 |
46 |
0,32 |
0,155 |
|
5 |
150 |
49 |
0,35 |
0,165 |
|
6 |
105 |
52 |
0,45 |
0,115 |
|
7 |
115 |
55 |
0,55 |
0,175 |
|
8 |
100 |
58 |
0,65 |
0,185 |
|
9 |
105 |
61 |
0,75 |
0,195 |
|
10 |
115 |
64 |
0,78 |
0,205 |
|
11 |
110 |
67 |
0,85 |
0,305 |
|
12 |
120 |
70 |
0,15 |
0,405 |
|
13 |
130 |
73 |
0,95 |
0,505 |
|
14 |
140 |
76 |
0,66 |
0,605 |
|
15 |
150 |
79 |
0,88 |
0,705 |
Контрольные вопросы:
1. Поясните сущность позиционных систем счисления. Как представляется запись числа в таких системах путем разложения в степенной ряд?
2. Докажите целесообразность использования в ЭВМ двоичной системы счисления. Укажите другие системы счисления, применяемые в ЭВМ.
3. Сформулируйте общие правила перевода целых и дробных чисел из одной позиционной системы счисления в другую.
4. Сформулируйте правила сложения двоичных чисел.
5. Сформулируйте правила вычитания двоичных чисел.
6. Сформулируйте правила умножения двоичных чисел.
7. Сформулируйте правила деления двоичных чисел.
8. Каким образом производятся логические операции над двоичными числами?
Лабораторная работа № 3
«Методы построения таблиц истинности»
Цель работы: изучить основные методы построения таблиц истинности.
Теоретическое введение
Существует достаточно много способов построения таблиц истинности логических выражений. Мы рассмотрим два самых популярных из них: с помощью Microsoft Excel и программный метод построения таблиц истинности.
Построение таблиц истинности с помощью Microsoft
Excel
Ввод данных с помощью мастера функций.
1. Установите курсор в ячейку таблицы, в которую надо ввести данные.
2. Щелкните левой кнопкой мыши на кнопке ![]() строки
строки
формул.
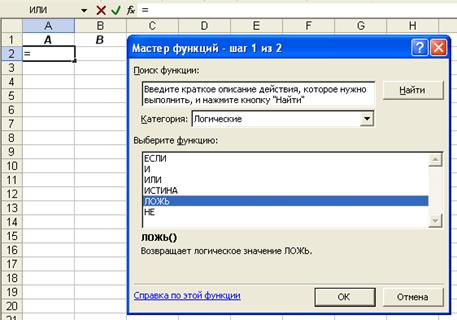
3. Выберите в окне списка Категория пункт
Логические и в окне списка Функции пункт с именем нужной функции:
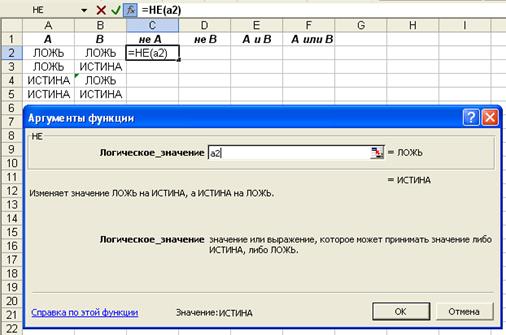 |
 |
Снова нажмите ОК. В указанной вами ячейке
появится значение функции ИСТИНА, что соответствует логической единице.
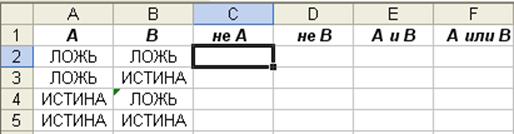
Подобным образом заполните таблицу истинности, найдя значения функций ![]() ,
,![]() , А&В, АvВ.
, А&В, АvВ.
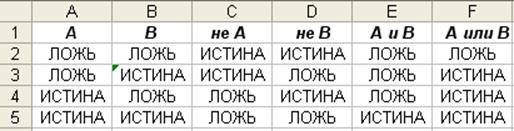
Примечание: выбрать ячейку, значение которой выбирается в качестве аргумента
функции, можно одним из двух способов: а) ввести имя ячейки с клавиатуры; б)
щелкнуть левой кнопкой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.