Моделирования систем: Методические указания к выполнению лабораторных работ

первом слое, используя функцию rands, то надо ввести следующую последовательность операторов:

net.layers{1}.initFcn = 'initwb';

net.inputWeights{1,1}.initFcn = 'rands';

net.biases{1,1}.initFcn = 'rands';

net.biases{2,1}.initFcn = 'rands';

net = init(net);

Практическое занятие 2.  Моделирование сети. Линейные сети

2.1. Статические сети. Статическая нейронная сеть характеризуется тем, что в ее

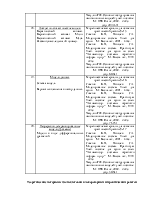
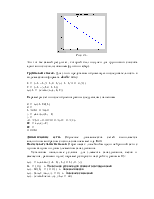
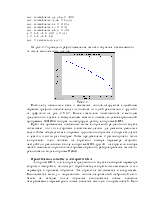
составе нет элементов запаздывания и обратных связей. Ее поведение не зависит от типа вектора входа, поскольку последовательно подаваемые векторы можно рассматривать как действующие одновременно или как один объединенный вектор. Поэтому в качестве модели статической сети рассмотрим сеть, показанную на рис. 1.

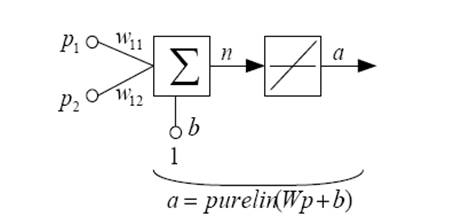
Рис.1.

Это однослойная сеть с двухэлементным вектором входа и линейной функцией активации. Для задания такой сети предназначена М- функция newlin из ППП Neural Network Toolbox, которая требует указать минимальное и максимальное значение для каждого из элементов входа; в данном случае они равны -1 и 1 соответственно, а также

количество слоев, в данном случае 1 .

net = newlin([-l 1; -1 1], 1);

Определим весовую матрицу и смещение равными W = [1 2], b = 0, и зададим эти значения, используя описание структуры сети

net.IW{l,l} = [1 2]; % Присваивание значений весов

net.b{l} = 0; % Присваивание значения смещения

Предположим, что на сеть подается такая последовательность из четырех векторов входа:

Поскольку сеть статическая, можно перегруппировать эту последовательность в следующий числовой массив:

Р = [-1 0 0 1; 0 -1 1 -1];

Теперь можно моделировать сеть:

А = sim(net,P) % Моделирование сети net с вектором входа Р и выходом А

А = -1 -2 2 -1

Результат нужно интерпретировать следующим образом. На вход сети подается последовательность из четырех входных сигналов, и сеть генерирует вектор выхода из четырех элементов. Результат был тот же самый, если бы имелось 4 одинаковых сети, функционирующих параллельно, и на каждую сеть был подан один из векторов входа и генерировался один из выходов.

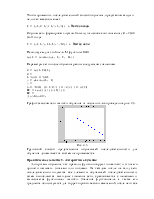
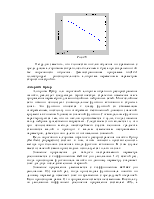
2.2. Динамические сети. Когда сеть содержит линии задержки, вход сети надо рассматривать как последовательность векторов, подаваемых на сеть в определенные моменты времени. Чтобы пояснить этот случай, рассмотрим простую линейную сеть, которая содержит 1 элемент линии задержки (рис. 2).

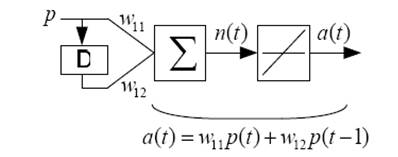
Рис.2.

Построим такую сеть:

% Создание однослойной линейной сети с линией задержки [0 1]

net = newlin([-l 1], 1, [0 1]);

Зададим следующую матрицу весов W = [1 2] и нулевое смещение:

net.IW{l,l} = [1 2]; % Присваивание значений весов

net.biasConnect =0; % Присваивание значений смещений

Предположим, что входная последовательность имеет вид {-1,-1/2,1/2,1}, и зададим ее в виде массива ячеек

Р = {-1 -1/2 1/2 1};

Теперь можно моделировать сеть, используя метод sim:

А = sim(net,P) % Моделирование сети net с входным сигналом Р и выходом А

А = [-1] [-5/2] [-1/2] [2]

Действительно,

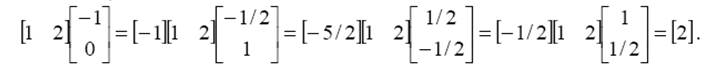
Введя массив ячеек, содержащий последовательность входов, сеть сгенерировала массив ячеек, содержащий последовательность выходов. В данном случае каждый выход формируется согласно соотношению

a(t)=p(t) + 2p(t – l).

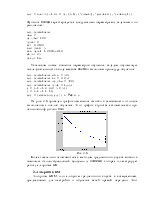
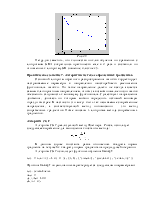
При изменении порядка следования элементов во входной последовательности будут изменяться значения на выходе. Если те же самые входы подать на сеть одновременно, то получим совершенно иную реакцию. Для этого сформируем следующий вектор входа:

р = [-1 -1/2 1/2 1];

После моделирования получаем:

А = sim(net, P) % Моделирование сети

А = -1 -1/2 1/2 1

Результат такой же, как если применить каждый вход к отдельной сети и

вычислить ее выход. Поскольку начальные условия для элементов запаздывания не указаны, то по умолчанию они приняты нулевыми. В этом случае выход сети равен

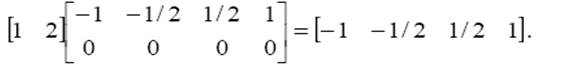
Процесс обучения нейронных сетей

Как только начальные веса и смещения нейронов установлены пользователем или с помощью датчика случайных чисел, сеть готова для того, чтобы начать процедуру ее обучения. Процесс обучения требует набора примеров ее желаемого поведения - входов р и желаемых (целевых) выходов t; во время этого процесса веса и смещения настраиваются так, чтобы минимизировать некоторый функционал ошибки. По умолчанию в качестве такого функционала для сетей с прямой передачей сигналов принимается среднеквадратичная ошибка между векторами выхода a и t:

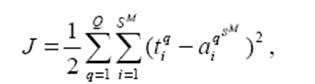
где J - функционал; Q - объем в

апрыборки; М - число слоев сети; q - номер выборки; S^M - число нейронов