Метрология, стандартизация и сертификация: Методическое пособие по выполнению лабораторных, практических и расчётно-графических работ

факторов, действие которых на практике не устранено, не учтено или не распознано. Выявление и оценка систематических погрешностей представляют особые трудности. Наблюдатель в ряде случаев даже не подозревает об их сущест­вовании. Именно систематические погрешности неоднократно яв­лялись причиной ошибочных научных выводов, создания некачест­венных конструкций изделий, массового брака изделий, непра­вильной настройки техники и т. п. В отличие от случайных погреш­ностей систематические погрешности могут быть определены, учтены или исключены. Систематические погрешности в большин­стве случаев могут быть определены экспериментальным путем, например, при поверке средств измерений. Именно систематиче­скую погрешность средств измерений определяют в основном при поверке средств измерений. По систематической погрешности судят о метрологической исправности средств измерений. Нежела­тельное влияние систематических погрешностей может быть ком­пенсировано введением поправок.

­Примеры:

1. Наблюдатель смотрит на шкалу измерительного прибора не строго пер­пендикулярно ее плоскости, а под некоторым углом к ней. При этом в отсчет показаний будет вноситься ошибка, которая будет зависеть от угла наблю­дения.

2. Специалист применяет манометр, у которого при отсутствии давления стрелка не устанавливается на нулевую отметку шкалы. В этом случае в ре­зультаты измерений вносится постоянная систематическая погрешность, которая может быть как положительной по знаку (стрелка правее нулевой отметки), так и отрицательной (стрелка левее нулевой отметки). Именно поэтому система­тические погрешности суммируются алгебраически, то есть с учетом их знаков.

Метрологические ор­ганы могут выдавать поправки на средства измерений с выявленными систематическими погрешностями. Обычно поправки вы­даются в форме таблиц, где указывается, какое значение поправ­ки нужно прибавить (или вычесть) в определенной точке отсчета результатов измерений.

случайные  погрешности

В отличие от систематических погрешностей, которые в той или иной степени могут быть выявлены и исключены, случайные погрешности устранить принципиально невозможно. Однако на основе методов теории вероятностей и математической статисти­ки можно уточнить значение полученного результата измерений и оценить его случайную погрешность. Всякий раз, когда результаты наблюде­ний формируются под действием большого числа независимо дейст­вующих факторов, каждый из которых оказывает лишь незначитель­ное действие по сравнению с суммарным действием всех остальных - распределение случайных погрешностей будет близко к нормальному, поэтому наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса:

­ p(x) =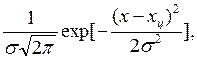

где:  s — параметр рассеивания распределения, равный СКО;

  х_ц— центр распределения, равный математическому ожиданию (среднему арифметическому).

В тех случаях, когда распределение случайных погрешностей приближается к нормальному, пользуются распределением Стьюдента. Распределение Стьюдента применяют при числе измерений n < 30, поскольку уже при n = 20, ..., 30 оно переходит в нормаль­ное.  Результат измерения записывается в виде:

Q = ± t×s;    P = Р_д,

где: Р_д — конкретное значение доверительной вероятности.

Распределение Стьюдента нашло широкое применение при статической обработке результатов многократных измерений.

Оценка параметра является точечной, если она выражается одним числом. Задача нахождения точечных оценок – частный случай статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выборки. Среднее арифметическое и σ_х (оценка СКО) являются точечными оценками. Такие оценки используют только при большом числе измерений. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной доверительной вероятностью Р находиться истинное значение оцениваемого параметра.

При оценке случайной по­грешности производят многократные измерения в одинаковых ус­ловиях, то есть измерения выполняют по одной и той же методи­ке, одними и теми же средствами измерений, при неизменных условиях. Пусть проведено п измерений (наблюдений) постоян­ной величины а и получены результаты наблюдений х₁, х₂, …, x_i, ...,  х_п, отличающиеся друг от друга. Это отличие обусловли­вается наличием случайных погрешностей. Полагаем, что система­тические и грубые погрешности отсутствуют. Статистическая обра­ботка результатов позволяет оценить как результаты измерений, так и их случайную погрешность. В качестве оценки результатов измерения принимается среднее арифметическое результатов на­блюдений:

                                    =.                                          (3.1)

Проведены три измерения одного и того же напряжения, то есть, как говорят, проведены три наблюдения и получены