

26.10.05 Доценко С.А.
Индивидуальный номер: 33 РТ5-22
Тема №3. Расчет коэффициента слойных потерь
Исходные данные
Таблица 1
|
V |
d |
c |
δ |
Δψ |
Δd |
Δc |
B |
|
мм/с |
мкм |
мкм |
мкм |
угл. мин. |
% |
% |
мм |
|
100 |
2,5 |
0,15 |
0,7 |
5 |
10 |
30 |
0,8 |
Требуется: рассчитать характеристику коэффициента слойных потерь, определить колебание величины магнитного потока (дБ) в магнитной головке на частоте 1 кГц;
Решение: Составим таблицу, в которую впишем искомые и промежуточные данные (табл.2).
Таблица 2
|
d/λ |
0 |
0,013 |
0,025 |
0,1 |
0,175 |
0,25 |
0,325 |
0,4 |
0,475 |
0,55 |
0,625 |
0,7 |
0,775 |
0,85 |
0,925 |
1 |
|
ƒ, кГц |
0 |
0,5 |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
28 |
31 |
34 |
37 |
40 |
|
λ, мкм |
∞ |
200 |
100 |
25 |
14,3 |
10 |
7,7 |
6,3 |
5,3 |
4,5 |
4 |
3,6 |
3,2 |
2,9 |
2,7 |
λ=d=2,5 |
|
Kd |
1 |
0,962 |
0,925 |
0,742 |
0,607 |
0,504 |
0,426 |
0,366 |
0,318 |
0,28 |
0,25 |
0,225 |
0,204 |
0,186 |
0,172 |
0,159 |
Минимальное рассчитываемое
значение длины волны: λ = δ = 2,5 мкм (это крайний правый столбец
табл.2). При этом частота 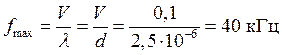 . На полученном
интервале от 0 до ƒmax выбираем отсчеты
частоты с равномерным шагом, находим длины волн, соответствующие выбранным
отсчетам частоты:
. На полученном
интервале от 0 до ƒmax выбираем отсчеты
частоты с равномерным шагом, находим длины волн, соответствующие выбранным
отсчетам частоты: 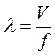 . Находим значения d/λ, а также рассчитываем коэффициент слойных потерь:
. Находим значения d/λ, а также рассчитываем коэффициент слойных потерь: 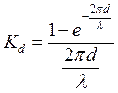 , графическая зависимость которого от
аргумента d/λ представлена на рис.1.
, графическая зависимость которого от
аргумента d/λ представлена на рис.1.


Рис.1. Волновая характеристика Kd Рис.2. Колебание Kd при изменении d на 10 %
на частоте 1 кГц
Определим колебание величины магнитного потока в магнитной головке (рис.2).
На частоте ƒ = 1 кГц отношение d/λ = 0,025, а Kd = 0,925. Для заданного Δd = 10 % от d (Δd = 0,25 мкм) найдем Kd.min и Kd.max на частоте 1 кГц:
Kd.min (d+ Δd) = 0,918
Kd.max (d– Δd) = 0,933
Нестабильность коэффициента слойных потерь составляет 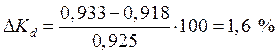 .
.
Колебание величины магнитного потока: 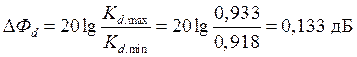 .
.
Тема №4. Расчет потерь неконтакта тракта записи-воспроизведения
Исходные данные берутся из табл.1.
Требуется: рассчитать характеристику коэффициента неконтакта, определить колебание коэффициента неконтакта (дБ) в магнитной головке на частоте 1 кГц.
Решение: Составим таблицу, в которую впишем искомые и промежуточные данные (табл.3).
Таблица 3
|
с/λ |
0,0001 |
0,0007 |
0,0015 |
0,075 |
0,15 |
0,225 |
0,3 |
0,375 |
0,45 |
0,525 |
0,6 |
0,675 |
0,75 |
0,825 |
0,9 |
1 |
|
ƒ, кГц |
0,1 |
0,5 |
1 |
50 |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
450 |
500 |
550 |
600 |
667 |
|
λ, мкм |
1000 |
200 |
100 |
2 |
1 |
0,667 |
0,5 |
0,4 |
0,333 |
0,286 |
0,25 |
0,222 |
0,2 |
0,182 |
0,167 |
λ=с=0,15 |
|
Kс |
1 |
0,995 |
0,991 |
0,624 |
0,39 |
0,243 |
0,152 |
0,095 |
0,059 |
0,037 |
0,023 |
0,014 |
0,009 |
0,006 |
0,004 |
0,002 |
Минимальное рассчитываемое
значение длины волны: λ = с = 0,15 мкм. При этом частота 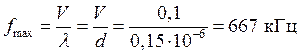 . На полученном интервале от 0 до ƒmax выбираем отсчеты частоты с равномерным шагом,
находим длины волн, соответствующие выбранным отсчетам частоты:
. На полученном интервале от 0 до ƒmax выбираем отсчеты частоты с равномерным шагом,
находим длины волн, соответствующие выбранным отсчетам частоты: 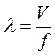 . Находим значения с/λ, а также
рассчитываем коэффициент неконтакта:
. Находим значения с/λ, а также
рассчитываем коэффициент неконтакта: ![]() , графическая
зависимость которого от аргумента с/λ представлена на рис.3.
, графическая
зависимость которого от аргумента с/λ представлена на рис.3.


Рис.3. Волновая характеристика Kс Рис.4. Колебание Kс при изменении с на 30 %
на частоте 1 кГц
Определим колебание коэффициента неконтакта (рис.4).
На частоте ƒ = 1 кГц отношение с/λ = 0,0015, а Kс = 0,991. Для заданного Δс = 30 % от с (Δс = 45 нм) найдем Kс.min и Kс.max на частоте 1 кГц:
Kс.min (с+ Δс) = 0,988
Kс.max (с– Δс) = 0,993
Нестабильность коэффициента слойных потерь составляет 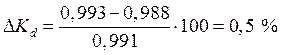 .
.
Колебание величины магнитного потока: 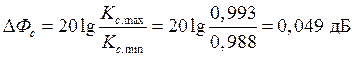 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.