
1. Синтез комбинационных схем в заданном схемотехническом базисе.
Процесс
синтеза схемы есть процесс представления исходной системы функций в виде
суперпозиции таких скалярных или векторных функций, каждая из которых
реализуется одним базисным элементом.
Задача синтеза комбинационной схемы из одновыход ных элементов может быть
сформулирована как задача представления исходной функции в виде суперпозиции
только скалярных функций, каждая из которых реализуется одним базисным
элементом. Например, если в качестве базисных выступают УЛМ (t), то задача синтеза сводится к
представлению реализуемых функций в виде суперпозиции функций, зависящих от не
более чем t аргументов. Если в качестве
базисных выступают ПЗУ
(t,s), то задача синтеза сводится к
представлению исходной функции (векторной или скалярной) в виде супер- позиции
векторных функций, зависящих от не более чем t переменных и имеющих не более чем sскалярных компонент. Если же
базисными являются ПЛМ (t,q,s) ТО задача синтеза
сводится к представлению исходной функции в виде суперпозиции таких ДНФ
векторiiых функций, каждая из которых реализуется одной ПЛМ (, щ, 8).
Так как базис программируемых элементов является функциональнополным
[33, 61], то решение задачи синтеза всегда существует — схема в базисе или УЛМ,
или ПЛМ, или в смешанных базисах программируемых элементов всегда может быть
построена. Важное практическое значение имеет сложность схемы, под
которой понимается обычно число базисных элементов ) Поэтому основной
рассматриваемой оптимизационной задачей синтеза будет минимизация сложности
схемы, другой важной характеристикой схемы является ее бьстродействие, определяемое
числом ее уровней. Максимальным быстродействием обладают одноуровневые схемы.
Удаление несущественных (фиктивных) аргументов функций
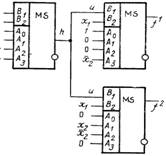
Рис. 15. Схема в базисе мультиплексоров
может
приводить к сокращению числа аргументов п к одiiоуровневым реализациям. Однако
такое сокращение не всегда возможно, поэтому основное внимание в гл. 2— 4
уделяется двухуровневым реализациям. Построение многоуровневых схем (см. гл. 5)
может быть проведено итер ативно н а основе двухуровневых декомпоз ицiтй. После
представления исходной функции в виде разложения векторных функций с
ограниченным числом переменных и компонент задача синтеза становится достаточно
простой — каждую из таких векторных функций можно непосредственно реализовать
одним ПЗУ или одноуровневой схемой из УЛМ или ПЛМ, поэтому основная трудность
заключается в построении таких разложений.
Пусть задана частичная векторная функция f(x)=f1(x), f2(x)), x=(x1,…x5) (табл. 19). Реализуем f(х) комбинационной схемой в базисах
УЛМ(3), мульти плексоров с двумя управляющими входами, ПЗУ (3, 2), ПЛМ (3, 4,
2). Так как все аргументы функции являются существенными *), то
уменьшить до трех число аргументов функции не удается и одноуровневая
реализация невозможна. Проведем двухуровневую декомпоз ицию (рис. 1.3) вида
f(x)=g(u, x1, x2), u=h(x3, x4,x5)
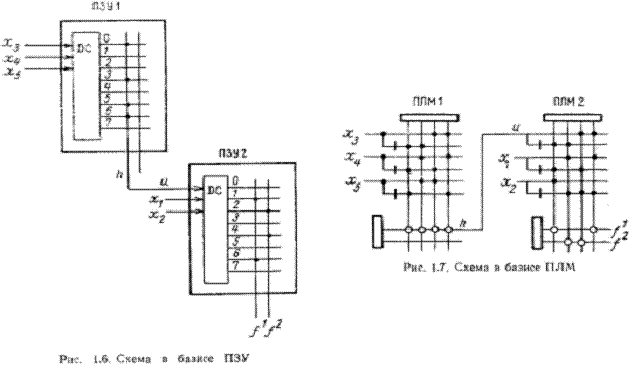
Функция h дана в табл. 1.10, функция —в табл. 1.11Так как каждая из функций h и g зависит от трех аргументов, то двухкомпонентная векторная функция g реализуется на втором уровне схемы двумя УЛМ (3), а скалярная функция h — одним УЛМ (3) (рис. 1.4). Каждый из УЛМ (3) может быть заменен мультиплексором, как это показано на рис. 1.5. Инверсные выходы мультиплексоров для данной схемы не используются, настройка мультiIплексоров является функциональной. Реализация функций h и g в базисе ПЗУ (3, 2) ведет к двухуровневой двухэлементной схеме, изображенной на рис. 1.6, а в базисе ПЛМ (3, 4, 2) к схеме, показанной на рис. 1.7.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.