Коэффициент фильтрации n-ой гармоники П-образной ЦС определяется следующим выражением:
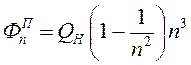 (5.11)
(5.11)
Рассчитаем полученные параметры для ЦС в базовой и
коллекторной цепях УМ, приняв добротность катушки индуктивности равной ![]() [3].
[3].
Определим
последовательный эквивалент параллельного соединения емкости ![]() ЦС и сопротивления нагрузки
ЦС и сопротивления нагрузки ![]() :
:
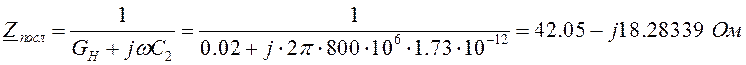
Откуда:
![]()
Согласно выражению (5.7):
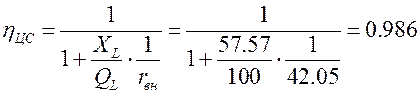
Нагруженная добротность по (5.9):
![]()
Относительна полоса пропускания ЦС по (5.10):
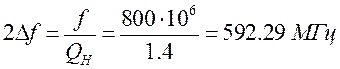
Поскольку ЦС в коллекторной цепи П-образная, используем для определения коэффициентов фильтрации формулу (5.12):
o
по
второй гармонике 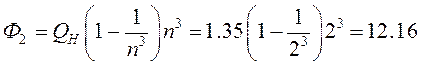
o
по
третьей гармонике 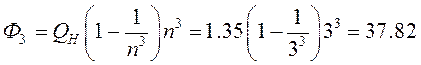
o по
четвертой гармонике 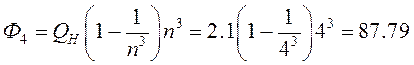
ЦС в базовой цепи.
3.Расчет сопротивлений ветвей согласующих цепей.
Условием реализуемости данной цепи является:
![]() (3.1.1)
(3.1.1)
В данном случае эти сопротивления равны:
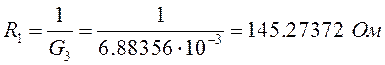 (3.1.2)
(3.1.2)
![]() (3.1.3)
(3.1.3)
Определим сопротивления в продольной и поперечной ветвях:
![]() (3.1.4)
(3.1.4)
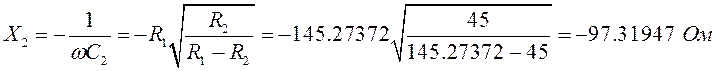 (3.1.5)
(3.1.5)
Номиналы элементов:
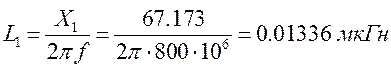 (3.1.6)
(3.1.6)
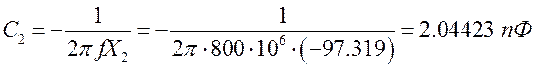 (3.1.7)
(3.1.7)
4.Учет в рассчитанных
сопротивлениях ветвей ЦС мнимых частей заданных ![]() и
и ![]() .
.
Пересчитаем мнимую часть выходного сопротивления предварительного УМ в состав проводимости поперечной ветви ЦС:
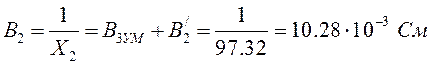 (4.1.1)
(4.1.1)
Откуда:
![]() (4.1.2)
(4.1.2)
С учетом этого номинал емкости в поперечной ветви имеет значение:
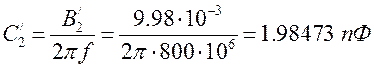 (4.1.3)
(4.1.3)
Пересчитаем мнимую часть входного сопротивления выходного УМ в состав сопротивления продольной ветви ЦС:
![]() (4.1.4)
(4.1.4)
Откуда:
![]() (4.1.5)
(4.1.5)
С учетом этого номинал индуктивности в продольной ветви имеет значение:
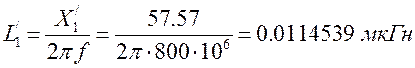 (4.1.5)
(4.1.5)
5.Оценка параметров ЦС.
Очевидно, представление колебательной мощности
генератора ![]() в виде двух составляющих: мощности потерь
в виде двух составляющих: мощности потерь ![]() и мощности в полезной нагрузке генератора
и мощности в полезной нагрузке генератора ![]() справедливо при использовании любой ЦС,
так как в его основе лежит фундаментальный закон природы – закон сохранения
энергии.
справедливо при использовании любой ЦС,
так как в его основе лежит фундаментальный закон природы – закон сохранения
энергии.
Любую ЦС можно характеризовать таким параметром, как отношение мощности в полезной нагрузке генератора, нагружающей ЦС, ко всей мощности, подводимой к ЦС, равной колебательной мощности генератора. Это отношение называют КПД ЦС:
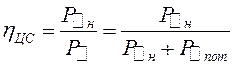 (5.1)
(5.1)
Выражение (5.1) можно представить в виде:
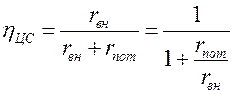 (5.2)
(5.2)
где ![]() -
активное сопротивление, вносимое полезной нагрузкой,
-
активное сопротивление, вносимое полезной нагрузкой,![]() - сопротивление собственных потерь
ЦС.
- сопротивление собственных потерь
ЦС.
Ненагруженная добротность ЦС определяется
параметрами ![]() ,
,![]() ,
,![]() :
:
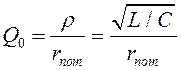 (5.3)
(5.3)
Нагруженная добротность контура![]() определяется с учётом активного сопротивления,
вносимого полезной нагрузкой:
определяется с учётом активного сопротивления,
вносимого полезной нагрузкой:
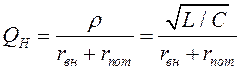 (5.4)
(5.4)
Ненагруженная добротность выражается через сопротивления реактивных элементов следующим образом:
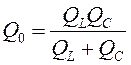 (5.5)
(5.5)
Добротность конденсаторов ![]() обычно на порядок выше, чем добротность
катушек индуктивности
обычно на порядок выше, чем добротность
катушек индуктивности ![]() . Следовательно, практически:
. Следовательно, практически:
![]() (5.6)
(5.6)
Представим выражение (5.2) в следующем виде:
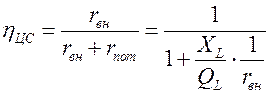 (5.7)
(5.7)
где
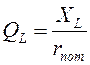 (5.8)
(5.8)
Исходя из выражений (5.2)-(5.4), получим:
![]() (5.9)
(5.9)
Одной из важных характеристик ЦС
является пропускаемая ей полоса частот![]() .
Реальные сигналы, используемые в радиотехнике, занимают некоторую полосу
частот, соответственно и ГВВ должен быть рассчитан на работу с таким сигналом.
Пропускаемая ЦС полоса частот с ослаблением относительно сигнала на резонансной
частоте по уровню – 3 дБ (уровень 0,707) связана с резонансной частотой контура
.
Реальные сигналы, используемые в радиотехнике, занимают некоторую полосу
частот, соответственно и ГВВ должен быть рассчитан на работу с таким сигналом.
Пропускаемая ЦС полоса частот с ослаблением относительно сигнала на резонансной
частоте по уровню – 3 дБ (уровень 0,707) связана с резонансной частотой контура![]() и его нагруженной добротностью
и его нагруженной добротностью![]() соотношением:
соотношением:
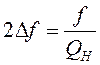 (5.10)
(5.10)
Коэффициент фильтрации n-ой гармоники Г-образной ЦС:
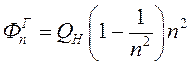 (5.11)
(5.11)
Рассчитаем
полученные параметры для ЦС в базовой и коллекторной цепи УМ, приняв
добротность катушки индуктивности равной ![]() [3].
[3].
Согласно выражению (5.7):
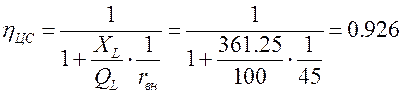
Нагруженная добротность по (5.9):
![]()
Относительна полоса пропускания ЦС по (5.10):
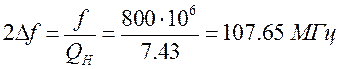
Поскольку ЦС в базовой цепи Г-образная, используем для определения коэффициентов фильтрации формулу (5.12):
o
по
второй гармонике 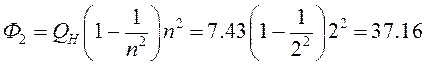
o
по
третьей гармонике 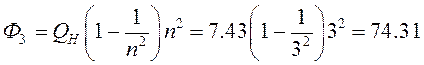
o
по
четвертой гармонике 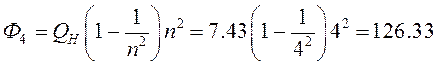
Cписок литературы
1. Вовченко П.С., Дегтярь Г.А.Устройства генерирования и формирования сигналов (радиопередающие устройства). Практикум для студентов: учеб.пособие. – Новосибирск: Изд-во НГТУ,2009. – 108с.
2. Проектирование радиопередающих устройств СВЧ: учеб.пособие для вузов / Г.М. Уткин, М.В. Благовещенский, В.П. Жуховицкая и др.; под ред. Г.М. Уткина. – M.: Сов. радио, 1979. – 320с.
3. Дегтярь Г.А. Устройства генерирования и формирования сигналов: учебное пособие / Г.А. Дегтярь. – 2-е изд., перераб. и доп. – Новосибирск: Изд-во НГТУ,2007. – 998с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.