












































Совокупность орбиталей, которые имеют одинаковое значение главного квантового числа, называется энергетическим уровнем.
Энергетические уровни обозначаются большими буквами латинского алфавита.
|
Значение n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Обозначение уровня |
K |
L |
M |
N |
O |
P |
Q |
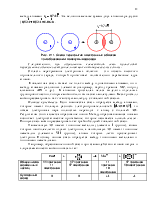
Б. Рассмотрим теперь систему, состоящую из
неподвижного ядра с зарядом ![]() и движущегося вокруг
него электрона. Если
и движущегося вокруг
него электрона. Если ![]() , то это атом водорода, при
, то это атом водорода, при ![]() система называется водородоподобным
ионом. Такой электрон обладает потенциальной энергией [см. формулу (2.4)]
система называется водородоподобным
ионом. Такой электрон обладает потенциальной энергией [см. формулу (2.4)]
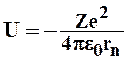 ,
,
где ![]() - расстояние между
электроном и ядром;
- расстояние между
электроном и ядром; ![]() - заряд электрона и протона;
- заряд электрона и протона; ![]() - количество протонов в ядре.
- количество протонов в ядре.
|
|
Состояние электрона также
описывается некоторой волновой функцией При этом в качестве параметров в
уравнение будет входить не только полная энергия |
зависящая от момента импульса
электрона ![]() ,собственные значения которого вычисляются
по формуле:
,собственные значения которого вычисляются
по формуле:
![]() , (2.12)
, (2.12)
где ![]() - целое число:
- целое число: ![]() .
.
Снова получается набор целочисленных значений параметра,
определяющего момент импульса, а также энергию частицы. Однако в отличие от ![]()
![]() может принимать и
нулевое значение. Это объясняется тем, что движение по кругу не ограничено.
Величина
может принимать и
нулевое значение. Это объясняется тем, что движение по кругу не ограничено.
Величина ![]() называется орбитальным квантовым числом.
На одном энергетическом уровне могут находиться орбитали (электронные облака),
имеющие различные геометрические формы.
называется орбитальным квантовым числом.
На одном энергетическом уровне могут находиться орбитали (электронные облака),
имеющие различные геометрические формы.
Форма орбиталей характеризуется орбитальным квантовым
числом ![]() .
.
Для орбиталей энергетического уровня ![]() орбитальное квантовое число
орбитальное квантовое число ![]() принимает значения от
принимает значения от ![]() до
до ![]() (табл. 2.1).
(табл. 2.1).
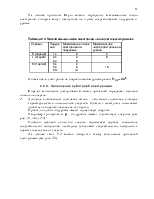
Таблица 2.1. Связь между главными и орбитальными квантовыми числами
|
Уровень |
Главное квантовое число |
Значения орбитальных квантовых чисел |
|
K |
1 |
0 |
|
L |
2 |
0 ,1 |
|
M |
3 |
0, 1, 2 |
|
N |
4 |
0, 1, 2, 3 |
Орбитали, для которых ![]() , имеют
форму шара и называются
, имеют
форму шара и называются ![]() - орбиталями
- орбиталями
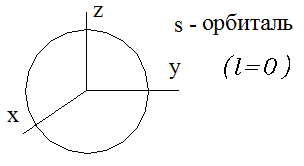
![]() - орбитали, как видно из табл. 2.1, имеются на всех энергетических уровнях.
- орбитали, как видно из табл. 2.1, имеются на всех энергетических уровнях.
На ![]() - уровне (на первом
энергетическом уровне) имеется только
- уровне (на первом
энергетическом уровне) имеется только ![]() - орбиталь.
- орбиталь.
Орбитали, для которых ![]() , имеют
форму гантели (объемной восьмерки) и называются
, имеют
форму гантели (объемной восьмерки) и называются ![]() -орбиталями.
-орбиталями.
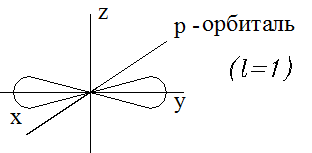
![]() -
орбитали имеются на всех энергетических уровнях, кроме первого (К)
уровня.
-
орбитали имеются на всех энергетических уровнях, кроме первого (К)
уровня.
Орбитали с большими
значениями ![]() имеют более сложную форму и обозначаются
так:
имеют более сложную форму и обозначаются
так:
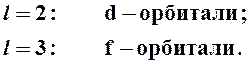
![]() -
орбитали есть на всех энергетических уровнях, кроме первого (К) и
второго (L) уровней.
-
орбитали есть на всех энергетических уровнях, кроме первого (К) и
второго (L) уровней.
![]() -
орбитали есть на всех энергетических уровнях, кроме первого (К),
второго (L) и третьего (М)
уровней. Энергия орбиталей, которые находятся на одном энергетическом уровне,
но имеют различную форму (различные квантовые орбитальные числа
-
орбитали есть на всех энергетических уровнях, кроме первого (К),
второго (L) и третьего (М)
уровней. Энергия орбиталей, которые находятся на одном энергетическом уровне,
но имеют различную форму (различные квантовые орбитальные числа ![]() ), неодинакова:
), неодинакова:
![]() .
.
Поэтому энергетические уровни состоят из энергетических подуровней.
![]() Энергетический подуровень – это совокупность орбиталей,
которые находятся на одном энергетическом уровне и имеют одинаковую форму.
Энергетический подуровень – это совокупность орбиталей,
которые находятся на одном энергетическом уровне и имеют одинаковую форму.
Таким образом, орбитали
одного подуровня имеют одинаковые значения главного квантового числа ![]() и одинаковые значения орбитального квантового
числа
и одинаковые значения орбитального квантового
числа ![]() .
.
Энергетический подуровень
обозначается так: главное квантовое число записывается арабской цифрой,
орбитальное квантовое число записывается соответствующей латинской буквой ![]() . Например,
. Например, ![]() -
-
![]() - подуровень первого
энергетического уровня
- подуровень первого
энергетического уровня ![]() ;
; ![]() - d - подуровень
четвертого энергетического уровня
- d - подуровень
четвертого энергетического уровня ![]() .
.
Число значений ![]() для каждого уровня равно главному
квантовому числу (см. табл. 2.1). Поэтому число подуровней на уровне тоже равно
главному квантовому числу.
для каждого уровня равно главному
квантовому числу (см. табл. 2.1). Поэтому число подуровней на уровне тоже равно
главному квантовому числу.
Орбитали на каждом
подуровне различаются не только формой, но и ориентацией в пространстве,
которая определяется так называемым магнитным квантовым числом. Проекция
орбитального момента импульса (2.12) на ось (например, ось ![]() ) записывается в виде:
) записывается в виде:
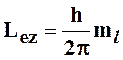 ,
,
где ![]() - магнитное квантовое
число. Оно может принимать значения:
- магнитное квантовое
число. Оно может принимать значения:
![]() , (2.13)
, (2.13)
иначе: от ![]() через
через ![]() до
до
![]() .
.
![]() Магнитное квантовое число
Магнитное квантовое число ![]() характеризует
расположение орбитали (электронного облака) в пространстве.
характеризует
расположение орбитали (электронного облака) в пространстве.
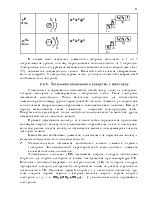
Число значений ![]() определяет число
орбиталей на подуровне (рис. 2.1). Оно равно:
определяет число
орбиталей на подуровне (рис. 2.1). Оно равно:
![]() .
.
Таким образом, квантовые числа определяют движение электрона:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.