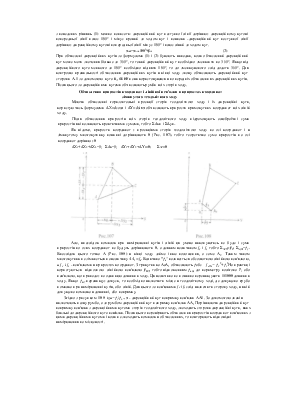


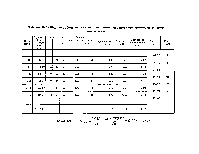


Якщо ƒвід перевищує допуск, то необхідно визначити місце в теодолітному ході, де допущена груба помилка при вимірюванні кутів, або ліній. Для цього за нев'язкими fx і fy слід визначити сторону ходу, в якій допущена помилка в довжині, або напрямку.
Згідно з рисунком 108 tga=ƒу/ƒx-, α - дирекційний кут напрямку нев'язки АА1. За допомогою знаків визначають назву румба, а за румбом дирекційний кут напрямку нев'язки АА1 Порівнюючи дирекційний кут напрямку нев'язки з дирекційними кутами сторін теодолітного ходу, знаходять сторони дирекційні кути, яких близькі до дирекційного кута нев'язки. Після цього перевіряють обчислення приростів координат пов'язаних з цими дирекційними кутами і коли не знаходять помилок в обчисленнях, то повторюють відповідні вимірювання на місцевості.
Якщо відносна нев'язка не перевищує допуск, то нев'язки в приростах координат розподіляють по приростах пропорціонально до довжини ліній з протилежним знаком так, щоб після розподілу нев'язок суми приростів координат дорівнювали "0", тобто ΣΔХП=0; Хдуп=0,
ΣΔУП =0. Для цьоro визначають поправку на 1 метр довжини лінії. З цією метою величини нев'язок ділять на периметр полігона δХ =-ƒ, δу=-ƒу/Р, а потім визначають поправку на всю довжину лінії δхі=-ƒх/Рdi; δvj=-ƒ/Рdi..В тих випадках, коли нев'язки ƒх і ƒу за абсолютною величиною малі, то обчислюють поправки не на 1 м довжини лінії, а на 100 м, тому що на 1 м ці поправки дуже малі, тоді δХі = -ƒх100/Рdi; δуі = -ƒу100/Рdi,
Додаючи алгебраїчно обчислені поправки δхі, δуі до обчислених приростів координат, одержимо виправлені прирости координат.
ΔХ1 =ΔX1'+ -ƒx/Рd1; ΔYl =ΔY1' + -ƒу/Рd1
ΔХ2 = ΔХ'2 + -ƒх/Рd2; ΔY2 = Y2' + -ƒy/Рd2
В приведених формулах:
ΔХ1'; ΔХ2'...обчислені прирости координат
ΔУ1; ΔУ2'... обчислені прирости координат
ΔХ1; ΔХ2...виправлені прирости координат
ΔУ1; ΔУ2... виправлені прирости координат
Сума виправлених приростів координат в зімкнутому полігоні повинна дорівнювати "0", тобто теоретичній сумі приростів.
Маючи виправленні прирости координат, обчислюють координати всіх точок ходу за правилом: координата наступної точки дорівнює координаті попередньої точки плюс приріст координат.
Xn+1=Xn+ΔXn; Yn-H=Yn+1+ΔYn
Для контролю правильності обчислення координат в зімкнутому теодолітному ході необхідно до координати останньої точки Хn і Уn додати відповідні прирости ΔХn і ΔYn і обчислити координати вихідної точки.
Обчислення розімкнутих теодолітних ходів Обчислення кутової нев'язки
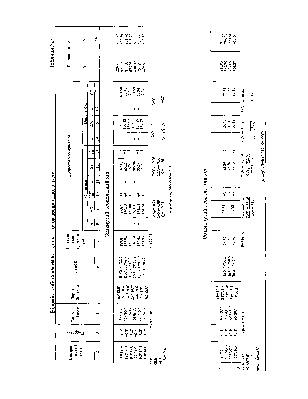
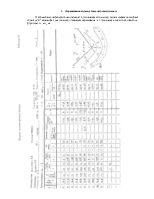
Обчислення кутової невязки в розімкнутому теодолітному ході виконується так само, як і в зімкнутому ході. Спочатку підраховують суму всіх виміряних кутів (Таблиця 7 графа 2), тобто: Σвп=βа+Рі+Р2+...+Рп- Після цього, розв'язуючи обернені геодезичні задачі, за відомими координатами вихідних пунктів А, С, В, Д обчислюють дирекційні кути вихідних сторін СА і ВД.
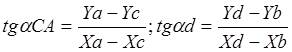 |
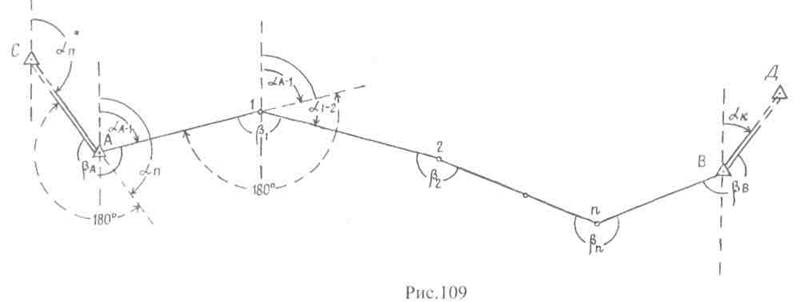
Знаючи початковий дирекційний кут αп=αСА, згідно Рис.109, можна обчислити дирекційні кути всіх наступних сторін ходу: αА-1=αп+180°-βА
α1-2=αА+180о-β1
..........................
αк=αп-в+180°-βв
Додавши всі ці рівняння почленно і скоротивши одержимо:
αк =αп +180°n-Σβ або Σβт=αn+180°п-ак
За цією формулою обчислюється теоретична сума кутів в розімкнутому теодолітному ході для кутів лежачих справа за ходом. Якщо в теодолітному ході вимірювались кути лежачі зліва за ходом, то застосовується формула: Σβт= ак + 180° п-ап, де п - кількість кутів в теодолітному ході.
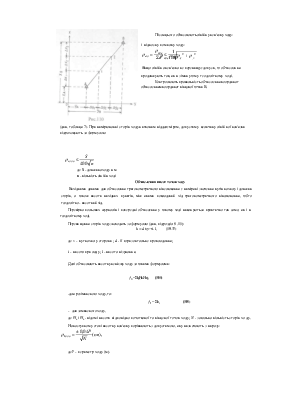
Маючи Σβп і Σβт підраховують величину кутової нев'язки ƒβ=Σβп-Σβт- Одержану нев'язку порівнюють з допустимою, яка підраховується за формулою
кути з оберненим знаком δК = -ƒβ/nПісля введення поправок в виміряні кути Σβп повинна дорівнювати Σβт.
Обчислення дирекційних кутів і румбів сторін розімкнутого теодолітного ходу
За виправленими кутами обчислюють дирекційні кути і румби всіх
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.