Лекція № 20. Зрівнювання теодолітних ходів.
План лекції:
1. Мета зрівнювальних робіт.
2. Зрівнювання системи теодолітних ходів з одною вузловою точкою.
1. Мета зрівнювальних робіт
Для виконання топографічних зйомок на місцевості створюють геодезичну знімальну основу, прокладаючи теодолітні та нівелірні ходи. Ці ходи будуть спиратися на вихідні планові і висотні пункти старших класів, які вважаються безпомилковими.
Вони також будуть перетинатися, утворюючи одну або декілька вузлових точок або зімкнені полігони. Якби вимірювання були безпомилковими, то кожна обчислена точка (координата або відмітка) теодолітного або нівелірного ходів від будь-якої вихідної точки в будь-якому напрямі мала би одне й те саме значення.
Але тому, що вимірювання супроводжується випадковими та систематичними помилками, обчислені координати або відмітки одної і тої точки з різних ходів будуть мати різні значення, які відрізняються одне від одного на невеликі величини.
Така невизначеність недопустима тому, що нам необхідно знати найімовірніше значення вимірюваної величини, щоб одержати однозначні значення координат або відміток точок теодолітного або нівелірного ходів їх необхідно зрівнювати.
Сутність зрівнювання полягає в обчисленні поправок до виміряних величин, щоб координати або відмітки точок обчислені за виміряними величинами з урахуванням поправок задовольняли необхідним висунутим до них вимогам, тобто не змінювали свого значення.
2. Зрівнювання системи теодолітних ходів з одною вузловою точкою
Зрівнювання системи теодолітних ходів виконують в такій послідовності:
1. Складають схему прокладених теодолітних ходів (Рис. 1), на яку з польових журналів виписують значення виміряних кутів, довжини ліній, нумерують ходи, показують стрілками напрями ходів і намічають одну із ліній, яка прилягає до вузлової точки. Цю лінію приймають за вузлову (лінія 4-5).
2. Виписують із схеми у відомість обчислення координат у відповідні графи виміряні кути, довжини ліній, дирекційні кути вихідних ліній та координати вихідних точок.
|
|
3. Вибравши вузлову лінію, наприклад, лінію 4-5, підраховують суми виміряних кутів по кожному ходу: Σβ1, Σβ2, Σβ3.
4. По всіх трьох ходах обчислюють значення дирекційного кута вузлової лінії 4-5. Обчислення ведуть за формулами:
α'4-5 = αДА + 1800 n1 - Σβ1
α"4-5 = αРВ + 1800 n2 - Σβ2
α"'4-5 = αЕС + 1800 n3 - Σβ3,
n1; n2; n3 - число кутів у кожному ході.
Якщо в теодолітних ходах виміряні кути розташовані зліва за ходом, тоді обчислення дирекційного кута вузлової лінії виконують за формулою:
αК = αП + Σβ - 1800n
5. Із обчислених трьох значень дирекційних кутів вузлової лінії 4-5 обчислюють її найімовірніше значення.
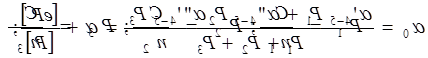 |
Для зручності обчислень "с" взято рівним 20. Схема обчислення найімовірнішого значення дирекційного кута лінії 4-5 і оцінки точності приведена в таблиці 25.
|
|
Таблиця 25.
6. Обчислюють кутові нев'язки в ходах, користуючись формулами:
fβ1 = α0 - α'4-5, fβ2 = α0 - α''4-5, fβ3 = α0 - α'''4-5 - якщо в ходах виміряно кути, які розташовані справа за ходом і fβі = αі' - α0 якщо в ходах виміряно кути, розташовані зліва за ходом.
|
|
7. За обчисленими нев'язками виконують оцінку точності вимірювання кутів.
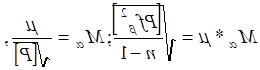 |
де n - число ходів в системі.
8.
де n - число кутів в ходу.
9. За виправленими кутами і дирекційними кутами вихідних ліній обчислюють дирекційні кути всіх ліній в ходах.
10. Користуючись формулами: Δх=dcosα; Δy=dsinα обчислюють прирости координат по всіх сторонах ходів.
11. Підраховують суми обчислених приростів координат по кожному ходу:
[Δx1]; [Δy1]; [Δx2]; [Δy2]; [Δx3]; [Δy3] і довжини ходів [d1], [d2], [d3].
12. За координатами вихідних пунктів і сумах приростів координат по ходах обчислюють координати вузлової точки Х5 і У5 по кожному ходу (таблиця 26).
X'5 = XA + [ΔX1], Y'5 = YA + [ΔY1]
X''5 = XB + [ΔX2], Y''5 = YB + [ΔY2]
X'''5 = XC + [ΔX3], Y'''5 = YC + [ΔY3]
|
|
13.
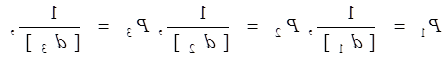 |
А також обчислюють їх суми.
14. Обчислюють найімовірніше значення координат вузлової точки за формулами:
15.
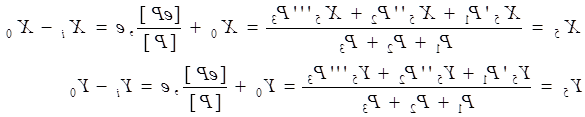 |
fX1 = X5' - X5 fY1 = Y5' - Y5
fX2 = X5'' - X5 fY2 = Y5'' - Y5
fX3 = X5''' - X5 fY3 = Y5''' - Y5
16. Виконують оцінку точності обчислення найімовірнішого значення координат вузлової точки. Обчислюють середню квадратичну помилку одиниці ваги μ і середню квадратичну помилку координат М.
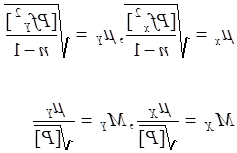 |
де n в - число ходів.
17. Величина нев'язок кожного ходу вписують у відомість обчислення координат точок теодолітних ходів і підраховують їх абсолютні і відносні величини по кожному ходу за формулами:
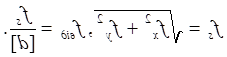 |
18. Якщо відносні помилки в ходах не перевищують допуски, то нев'язки в приростах координат розподіляють у відповідні прирости з оберненими знаками пропорційно довжинам ліній і підраховують суми виправлених приростів координат кожного ходу. Вони повинні дорівнювати різниці координат кінцевих точок, тобто:
[ΔX1вип] = X5 - XA [ΔY1вип] = Y5 - YA
[ΔX2вип] = X5 - XB [ΔY2вип] = Y5 - YB
[ΔX3вип] = X5 - XC [ΔY3вип] = Y5 - YC.
19. За виправленими приростами координат і вихідними координатами точок теодолітних ходів обчислюють координати всіх точок ходів. Контролем правильності обчислення координат точок є сходимість координат вузлової точки Х5 і У5, обчисленої в таблиці 26.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.