Вследствие циклического изменения температуры окружающего воздуха и величины солнечного баланса в течение суток принимаем, что нагрев и охлаждение рассола также будут осуществляться циклически. Число циклов принимаем равным числу суток в расчетном интервале. Тогда, при условии, что начальной температурой, от которой происходит нагрев рассола, является температура окружающего воздуха.
![]() ,
(11)
,
(11)
где
![]() – масса рассола, приходящегося на 1 м2
поверхности бассейна, кг;
– масса рассола, приходящегося на 1 м2
поверхности бассейна, кг;
![]() – теплоемкость рассола,
Дж/(кг×оС);
– теплоемкость рассола,
Дж/(кг×оС);
![]() – температура
окружающего воздуха, оС.
– температура
окружающего воздуха, оС.
При
уровне рассола в бассейне ![]() , м,
, м,
![]() .
(12)
.
(12)
Теплоемкость
рассола, если принять теплоемкость воды ![]() =4190 Дж/(кг×оС),
определяется по уравнению
=4190 Дж/(кг×оС),
определяется по уравнению
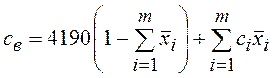 , (13)
, (13)
где
![]() – массовая доля
– массовая доля ![]() -го
компонента рассола, кг/кг;
-го
компонента рассола, кг/кг;
![]() – теплоемкость
– теплоемкость ![]() -го компонента рассола, Дж/(кг×оС).
-го компонента рассола, Дж/(кг×оС).
Уравнение (11) с учетом (12) представляется в виде
![]() .
(14)
.
(14)
Потери тепла в окружающую среду не представляется определить расчетным путем. Поэтому величину этих потерь, по нашему мнению, целесообразно представить следующим образом:
![]() ,
(15)
,
(15)
где
![]() – доля потерь тепла от поглощенной
энергии.
– доля потерь тепла от поглощенной
энергии.
Количество поглощенной 1 м2 поверхности бассейна энергии
![]() ,
(16)
,
(16)
где
![]() – продолжительность поглощения энергии в
течение суток, с.
– продолжительность поглощения энергии в
течение суток, с.
Для упрощения расчетов с учетом уравнения (15) зависимость (7) можно записать в виде
![]() ,
(17)
,
(17)
где ![]() –
количество эффективно поглощенной 1 м2 бассейна энергии, Дж/м2.
–
количество эффективно поглощенной 1 м2 бассейна энергии, Дж/м2.
![]() ; (18)
; (18)
![]() (19)
(19)
Из приведенных зависимостей следует, что скорость
испарения может быть определена путем совместного решения уравнений (10),(12),
(13), и (19) методом последовательных приближений. При этом задаются
температурой рассола ![]() . Условие сходимости при решении
– выполнение с заданной точностью равенства (24). С целью оптимизации задания
. Условие сходимости при решении
– выполнение с заданной точностью равенства (24). С целью оптимизации задания ![]() в первом приближении, сокращения числа
итераций и объема вычислений оценим максимально возможную температуру
в первом приближении, сокращения числа
итераций и объема вычислений оценим максимально возможную температуру ![]() , оС. Это температура, до
которой может быть нагрет рассол при выполнении следующего условия: количество
тепла
, оС. Это температура, до
которой может быть нагрет рассол при выполнении следующего условия: количество
тепла ![]() расходуется только на нагрев рассола.
Тогда
расходуется только на нагрев рассола.
Тогда
![]() .
(20)
.
(20)
При выполнении первой итерации можно принять ![]() несколько меньше
несколько меньше ![]() ,
например, на 0,5о.
,
например, на 0,5о.
Из анализа приведенных выше уравнений следует, что для проведения расчетов скорости испарения должны быть подготовлены и заданы следующие исходные параметры:
1) состав и плотность рассола;
2) глубина налива его в бассейн (глубина бассейна).
3)
свойства компонентов рассола (их
теплоемкость, коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() );
);
4) климатические условия для места проведения упаривания в расчетном месяце (температура воздуха, парциальное давление паров воды в нем, скорость ветра, величина солнечного баланса).
Состав рассола по результатам химических анализов
обычно представляется концентрациями составляющих его компонентов ![]() , кг/м3. Для расчетов по
уравнениям (4) и (13) концентрации пересчитываются в величины
, кг/м3. Для расчетов по
уравнениям (4) и (13) концентрации пересчитываются в величины ![]() и
и ![]() следующим
образом:
следующим
образом:
![]() ; (21)
; (21)
![]() , (22)
, (22)
где ![]() и
и ![]() – молярные массы воды и
– молярные массы воды и ![]() -го компонента рассола соответственно,
кг/кмоль;
-го компонента рассола соответственно,
кг/кмоль;
![]() –
массовая доля воды в рассоле, кг/кг.
–
массовая доля воды в рассоле, кг/кг.
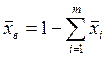 . (23)
. (23)
Приняв ![]() =18 кг/кмоль,
выражение (22) представим в виде
=18 кг/кмоль,
выражение (22) представим в виде
![]() . (24)
. (24)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.