Исследование спектров амплитудно-модулированных колебаний, страница 5

Рассчитаем спектр боковых частот по формуле: ω₀±kΩ, где

            ω₀- частота несущей;

            Ω – частота модулирующего сигнала;

            k – порядок гармоники.

1.  ω₀ + 1Ω = 200 ± 1x20 = 220 (180) kГц

2.  ω₀ + 2Ω = 200 ± 2x20 = 240 (160) kГц

3.  ω₀ + 3Ω = 200 ± 3x20 = 290 (140) kГц

4.  ω₀ + 4Ω = 200 ± 4x20 = 320 (120) kГц

М=5

Рассчитаем высоты гармоник S_i(t)=A₀J_i(M)

1.  S_i(t)=A₀J_i(M)=2x0.18=0.36

2.  S_i(t)=A₀J_i(M)=2х0.33=0.66

3.  S_i(t)=A₀J_i(M)=2х0.04=0.08

4.  S_i(t)=A₀J_i(M)=2х0.36=0.72

5.  S_i(t)=A₀J_i(M)=2х0.39=0.78

Получим спектр ЧМ колебаний. Сравним полученный спектр с результатами расчета.

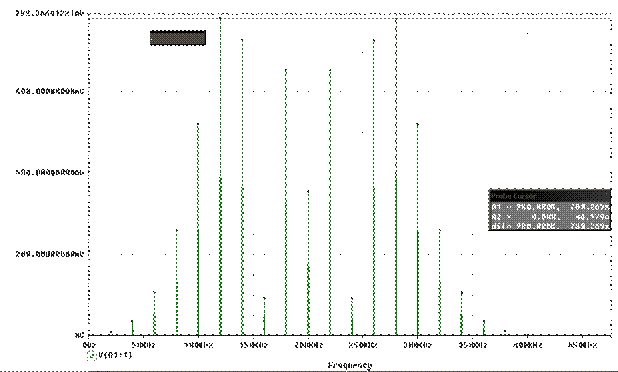
Рис. 2.3. Спектр ЧМ-колебаний

S(t) по экспериментальным данным	0.354	0.654	0.09	0.73	0.78
S(t) расчетная	0.36	0.66	0.08	0.72	0.78

М=3

Рассчитаем высоты гармоник S_i(t)=A₀J_i(M)

6.  S_i(t)=A₀J_i(M)=2x0.26=0.52

7.  S_i(t)=A₀J_i(M)=2х0.34=0.68

8.  S_i(t)=A₀J_i(M)=2х0.48=0.96

9.  S_i(t)=A₀J_i(M)=2х0.31=0.62

10.  S_i(t)=A₀J_i(M)=2х0.13=0.26

Получим спектр ЧМ колебаний. Сравним полученный спектр с результатами расчета.

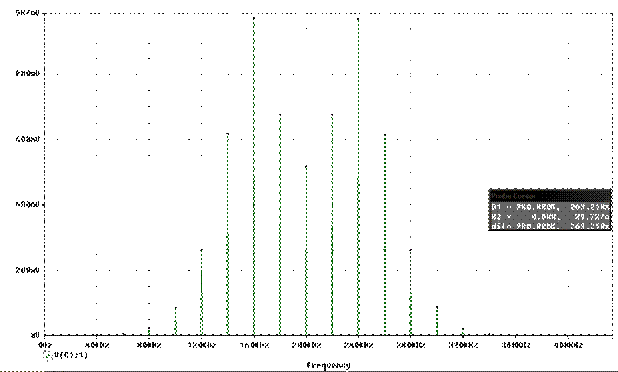
Рис. 2.4. Спектр ЧМ-колебаний

S(t) по экспериментальным данным	0.52	0.67	0.97	0.61	0.26
S(t) расчетная	0.52	0.68	0.96	0.62	0.26

Вывод: полученный спектр ЧМ колебаний практически совпадает с результатами расчета.

Лабораторная работа № 3

Исследование спектров импульсных сигналов

         Цель лабораторной работы

Целью лабораторной работы является изучение основных по­ложений преобразования Фурье, определение спектрально­го состава последовательности видеоимпульсов, определение спектрально­го состава  сигналов при импульсной модуляции.