Анализ системы автоматического управления, состоящей из 4-х элементов, страница 2

Передаточная функция ошибки по возмущению:

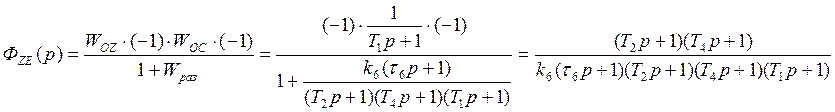
Ступенчатое воздействие:

;

;

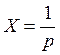
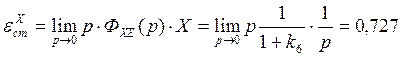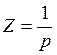
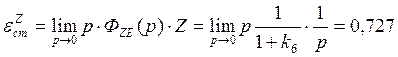Сигнал постоянной скорости:

.

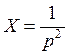
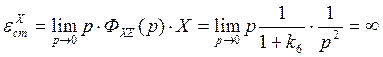1,7 Определим показатели качества переходных процессов, выполнив моделирование на ЭВМ по программе COMPAS. Для моделирования используется структурная схема, в которой все элементы представлены в виде типовых звеньев, содержащихся в программе COMPAS.

Переходные процессы получаем как реакцию системы на единичные ступенчатые задающие и возмущающие воздействия.

На рис.5 представлен график переходного процесса при подаче постоянного сигнала по управлению и возмущению, а на рис.6 представлен график переходного процесса при подаче сигнала постоянной скорости.

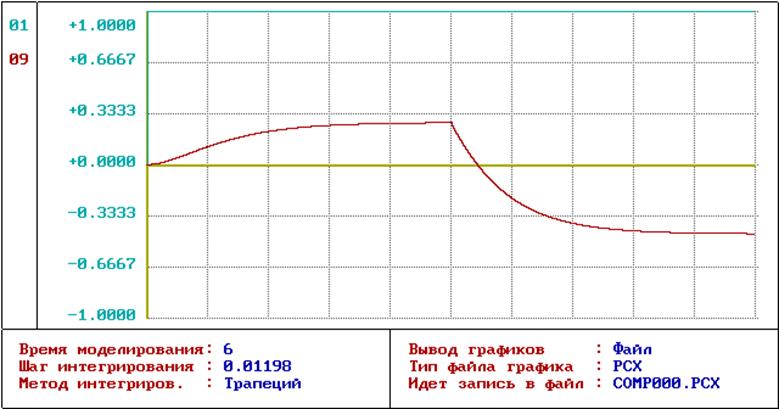
Рис. 5. График переходного процесса исходной системы при единичном ступенчатом задающем и возмущающем воздействиях

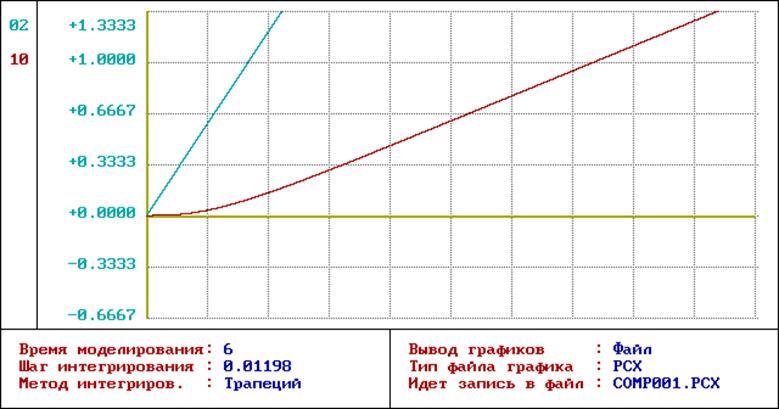
Рис. 6. График переходного процесса исходной системы при подаче сигнала постоянной скорости.

1.7.  Анализируя исходную систему, заключаем, что

1)  Время переходного процесса t_nn = 3с

2)  Перерегулирование отсутствует.

Глава 2. Синтез корректирующего звена.

Для того, чтобы система соответствовала нужным показателям по точности, и одновременно соблюдалось условие устойчивости необходимо произвести коррекцию исходной системы, т.е. ввести в цепь регулятора корректирующее звено.

Синтез корректирующего звена производят с помощью ЛАХ. Т.е. строим ЛАХ исходной системы и желаемую ЛАХ, а затем, вычитая из желаемой исходную, получим ЛАХ корректирующего звена По ней восстановим передаточную функцию корректирующего звена.

2.1 Построение ЛАХ исходной системы 

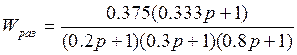 - передаточная функция исходной разомкнутой системы

Для построения ЛАХ исходной системы нам нужно построить ЛАХи типовых составляющих звеньев, а затем просуммировать их. Для усилительного звена определяем значение . Отмечаем это значение на оси ординат и проводим через эту точку прямую параллельно оси абсцисс.

Для апериодических звеньев также находим частоты среза, но лучи проводим под наклоном в -20дБ/дек.

                            

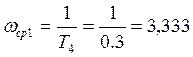
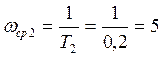
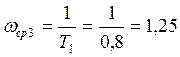
Для форсирующего звена находим частоту среза:

 

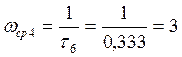
Откладываем это значение по оси частот в логарифмическом масштабе. Из полученной точки проводим луч под наклоном  +20 дБ/дек.

Суммируем последовательно, двигаясь от начала координат. Суммарная ЛАХ представлена жирной линией на рис. 7.

2.2  Построение желаемой ЛАХ

Желаемую ЛАХ (рис.7) строим по рекомендациям, т.е. строим такую ЛАХ, которая полностью удовлетворяет требованиям статического и динамического качества управления.

Алгоритм построения:

1)  Определяем частоту среза

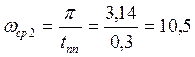
2)   Из точки  проводим среднечастотную связь с наклоном -20 дБ/дек.    Ограничения среднечастотной части -15-20 дБ.

3)   В низкочастотной части откладывается ордината 20lgK = 20lg 20 = 26

4)   В области высоких частот, т.к. она практически не влияет, то построение повторяет соответствующую ЛАХ исходной системы.

2.3  Нахождение ЛАХ корректирующего звена и восстановление передаточной функции корректирующего звена.

 ЛАХ корректирующего звена находим как разницу между желаемой ЛАХ и исходной (рис.7)

Восстанавливаем по графику передаточную функцию корректирующего звена:

                                            

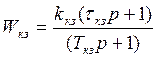
k_кз = 20log17.5 = 7.5

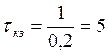
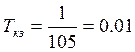
Однако в результате моделирования системы были найдены более благоприятные значения коэффициентов:

k_кз  = 53,333

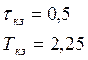
Тогда                                              

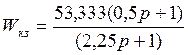
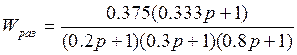
2.4Структурная схема скорректированной системы

Вставляем корректирующее звено в цепь исходной системы как последовательный элемент ,так как проводили последовательную коррекцию.

Вычислим установившиеся ошибки по задающему и возмущающему воздействиям, приняв для задающего ступенчатую и линейную функции, а для возмущающего только ступенчатую функцию. Статические ошибки определяем в процентном отношении к модулю ступенчатого воздействия и скорости изменения линейного воздействия.

Передаточная функция скорректированной системы:

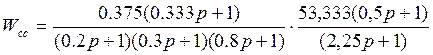
Передаточная функция ошибки по управлению:

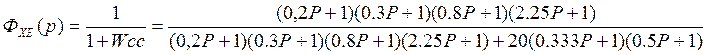
Передаточная функция ошибки по возмущению:

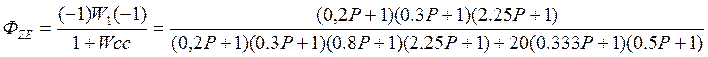
Ступенчатое воздействие:

;

;

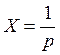
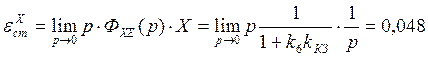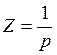
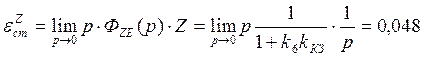Сигнал постоянной скорости:

.

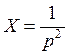
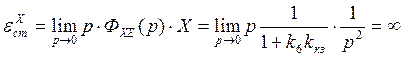Определим показатели качества переходных процессов скорректированной системы при ступенчатом единичном сигнале (рис.7) и при подачи сигнала постоянной скорости (рис.8).

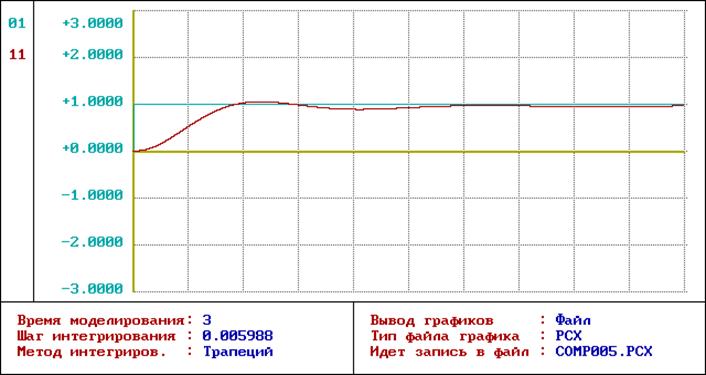
Рис. 7. График переходного процесса скорректированной системы при единичном ступенчатом задающем  воздействии

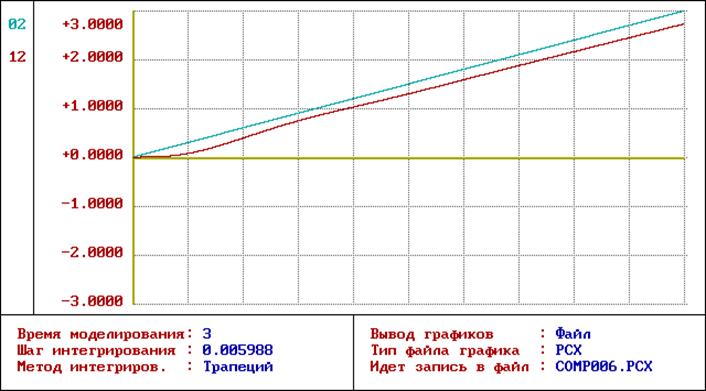
Рис. 6. График переходного процесса скорректированной системы при подаче сигнала постоянной скорости.

Вывод: в результате коррекции получили

              1.Быстродействие системы увеличилось с 3с до 0,6с.

              2.Статическая ошибка стала укладываться в пяти процентный продел.