Ітераційні методи розв’язання системи лінійних алгебраїчних рівнянь

Ітераційні методи розв’язання СЛАР

Розглянуті методи розв’язання СЛАР шляхом зведення до трикутного вигляду – метод послідовного виключення невідомих Гауса, за рекурентними формулами схеми Халецького і квадратного кореня – належать до класу так званих “точних методів”. Нажаль, характеристика “точний” у даному випадку не гарантує отримання точного розв’язку, а означає, що метод дозволяє за визначене число математичних операцій отримати точний розв’язок при умові відсутності похибки обчислень. На практиці, при використанні в обчисленнях на ЕОМ подання дійсних чисел з фіксованою кількістю розрядів завжди присутня похибка округлення а звідси і похибка обчислень. З збільшенням розмірів системи зростає кількість математичних операцій потрібних для її розв’язання і як наслідок похибка обчислень. У випадку так званих погано обумовлених систем похибка розв’язку отриманого за “точними” методами може виявитися неприйнятною.

Розроблені ітераційні методи розв’язання СЛАР, які дозволяють послідовно уточнювати розв’язок, починаючи з деякого наближення. Для цих методів також існують межі точності, яку можна досягнути при їх застосуванні, але вони можуть виявитися роботоспроможними , коли “точні” вже не працюють. Крім того, вони, у певних випадках, вимагають меншої пам’яті ЕОМ.

Метод простої ітерації

Перетворимо СЛАР        до еквівалентної системи       .  (1)

Виберемо початкове наближення розв’язку  і використаємо (1) як ітераційну формулу:

  ,                                               (2)

 за допомогою якої отримаємо послідовність наближень розв’язку    , 

Якщо ця послідовність збігається , то  є точним розв’язком (1) - і значить початкової системи.

Варіанти еквівалентних перетворень системи:

,             ,

де  - довільна матриця, а  -скаляр, від значень яких залежить збіжність методу.

Умови збіжності методу ітерацій:

(,    )

Тобто  послідовність наближень розв’язку буде збігатися, якщо при множенні на матрицю  у (1)  модуль вектора зменшується (іншими словами матриця  є оператором, що стискує): . Умова збіжності може бути визначена через норму матриці.

Норми векторів та матриць

Норму матриці можна визначити наступним чином:

,

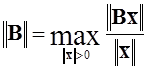де  є символом норми. Тобто норма матриці дорівнює максимальному значенню коефіцієнта збільшення норми векторів від множення на цю матрицю. В залежності від визначення норми векторів їм будуть відповідати такі норми матриць.

1.  Норма вектора визначається як його модуль: 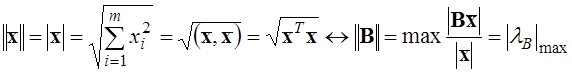, (3)

де  найбільше за модулем власне число матриці. Така норма матриці зветься спектральною.

2.  Норма вектора визначається як його найбільша за модулем координата:

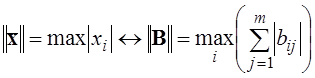 ,                                                       (4)

тобто норма матриці дорівнює максимальній з сум абсолютних значень елементів її рядків.

3.  Норма вектора визначається як сум абсолютних значень його координат:

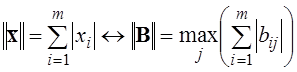,                                                            (5)

тобто норма матриці дорівнює максимальній з сум абсолютних значень елементів її стовпців.

Умовою збіжності :ітераційного процесу за формулою (2)    буде    , де норма обчислюється за однією з формул –(3), (4), або (5).

Метод Зейделя

Метод Зейделя заснований на наступному перетворенні системі рівнянь:

    ,

де: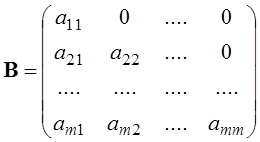;  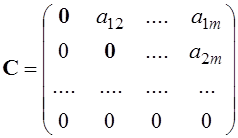           І       .

Відповідна ітераційна формула буде такою:

,

але, щоб не обчислювати обернену матрицю  , можна скористатися еквівалентною формулою:

,

Розв’язуючи в кожній ітераціі систему з трикутною матрицею.

Алгоритм методу Зейделя:

n:=0;    ;

цикл

обчислити   з        ;

n:=n+1;

до        або   n > n_max

Зв’язок задачі розв’язання СЛАР з симетричною додатно визначеною матрицею і мінімізації квадратичної форми

Матриця є симетрично, якщо  і додатно визначеною, якщо  при будь яких . Хоча СЛАР з такою матрицею є частинним випадком, вони зустрічають часто при розв’язанні прикладних задач. Для СЛАР з додатно визначеною матрицею розв’язок системи одночасно дає мінімум квадратичної форми:

і навпаки вектор, що мінімізує цю форму є розв’язком системи. Це дало основу для розробки так званих градієнтних методів які є ефективними при розв’язанні великих систем.

Метод найшвидшого градієнтного спуску

Метод найшвидшого градієнтного спуску побудований на пошуку наступного наближення за напрямом градієнту квадратичної форми:

,

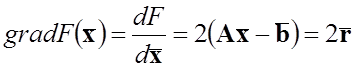так що:

,

при чому  визначається з умови мінімізації квадратичної форми на кожній ітерації:

.

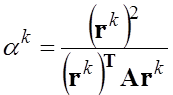Алгоритм методу найшвидшого градієнтного спуску:

k:=0;    ;

цикл

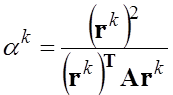;    ;         k:=k+1;

до 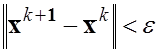       або   k > k_max

Метод спряжених градієнтів

За цим методом наступне наближення знаходиться на так званих А – ортогональних напрямах:

;    ,

при чому ці напрями обираються в площинах перпендикулярних поверхням рівня квадратичної форми:

.

Коефіцієнт  обчислюється з умови А – ортогональності:

,

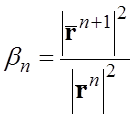а   -мінімуму квадратичної форми:

.

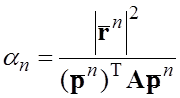Алгоритмметоду спряжених градієнтів: 

;     ;        ;       ;

цикл

;            ;

;         ;

;

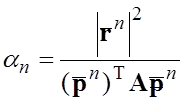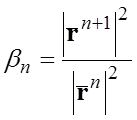до        або   n > n_max

Гр. K-2.

Лабораторна робота  N 7

Розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) за ітераційними методами.

Мета роботи : Навчитися розв’язувати системи лінійних алгебраїчних рівнянь з застосуванням ЕОМ за ітераційними методами.

Завдання  :

1. Скласти програму ЕОМ для розв’язання СЛАР за методом відповідно варіанту.

2.  Розв’язати дві СЛАР, матриця і праві частини яких були задані у лабораторній роботі N 6 (створюються програмами lr1AK2.exe та lr1bK2.exe відповідно варіанту).

3. Оцінити похибку значень невідомих.

Метод розв’язання СЛАР для варіантів:

1,4,7,10,13,16,19,22,25,28  - Зейделя;

2,5,8,11,14,17,20,23,26,29 - градієнтного спуску;

3,6,9,12,15,18,21,24,27,30 - спряжених градієнтів.

Методичні вказівки і вимоги до виконання роботи

Обчислення роботи виконуються на ЕОМ за створеною студентом програмою. Слід притримуватись структурного стилю програмування, виділяючи окремі кроки розв’язання задачі в окремі програмні модулі. Ці модулі доцільно робити універсальними і відповідно специфікувати  для можливості використання у подальших роботах і інших   курсах.

За результатами роботи оформлюється звіт, який повинен містити наступні розділи:

-  назву роботи;

-  мету;

-  конкретне завдання згідно варіанту;

-  конкретну схему розрахунків, що веде до розв’язання задачі і втілена у програмі ЕОМ;

-  текст програми ЕОМ;

-  результати з відповідними поясненнями і аналізом.

Звіт з роботи подається викладачу на перевірку. Якщо робота виконана з помилками, чи оформлення звіту не відповідає вимогам, він повертається для переробки. Умовою для зарахування роботи є наявність вірного звіту і спроможність студента відповісти на контрольні запитання.

Контрольні запитання

Поясніть сутність методу простої ітерації. Яка умова його збігання?

Поясніть сутність методу Зейделя. Яка умова його збігання?

Який зв’язок розв’язання СЛАР з мінімізацією квадратичної форми.

Поясніть сутність градієнтних методів розв’язку СЛАР.

Поясніть алгоритм методу найскорішого градієнтного спуску розв’язання СЛАР.

Поясніть алгоритм методу спряжених градієнтів розв’язання СЛАР.

Як практично оцінити похибку розв’язку СЛАР?

Як можна уточнити розв’язок СЛАР?

Що таке обумовленість СЛАР?

Які ви знаєте методи обчислення оберненої матриці?