Элементы и узлы ПЭВМ: Дешифраторы, шифраторы, мультиплексоры

Билет №16

Элементы и узлы ПЭВМ: Дешифраторы, шифраторы, мультиплексоры.

Дешифраторы

Дешифратором (избирательной схемой) называется ком-бинационная логическая схема без элементов памяти, в кото-рой определенная комбинация входных сигналов вызывает по-явление сигнала только на одной соответствующей выходной шине.

Пусть некоторая совокупность входных сигналов (цифро-вых кодов) выражается наборами  двоичных переменных . С помощью  переменных возможно образовать  различных кодов и, если требуется однозначно определить каждый из наборов переменных (кодов), дешифратор должен иметь  выходов. Такой дешифратор называется полным.

Условное обозначение дешифраторов на функциональных  схемах приведено на рис.4.11.

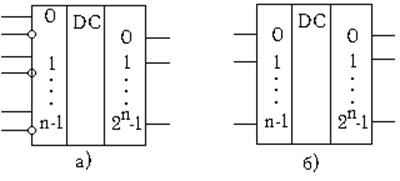
Рис.4.11. Условное обозначение дешифратора с парафазными входами(а) и с однофазными входами (б)

По способу логической организации дешифраторы делятся  на одноступенчатые (которые также называются линейны-ми, прямоугольными или матричными) и многоступенчатые,   которые, в свою очередь, подразделяются на секционные и пирамидальные.

Мультиплексоры

Мультиплексором на­зывается схема, осущест­вляющая передачу сигна­лов с одной из входных ли­ний в выходную. Выбор входной (информационной) линии производится кодом, поступающим на управляющие входы мульти­плексора. Мультиплексор с управляющими входа­ми  имеет 2^k информационных входов

Набор сигналов, поступающих на управляющие входы, за­дает двоичное число вида

 где – значение сигнала на входе. Выходной сиг­нал мультиплексора повторяет сигнал информационного входа D с номером X*.

Работа мультиплексора может иллюстрироваться контакт­ной схемой (рис. 3.20, а).

            Условное обозначение мультиплексо­ра, коммутирующего 2^k линий, показано на рис. 3.20, б.

Пример функциональной схемы мультиплексора с двумя управляющими входами дан на рис. 3.20, в.

Функция, реализуемая мультиплексором, может быть пред­ставлена в виде

где Rj — конъюнкция, равная 1 на наборе значений переменных

Рис. 3.20. Мультиплексор:

а — контактная модель; б — условное обозначение; в — функциональная схема

Xk-i Xk-2.. -Хо с номером / (т.е. на наборе, представляющем в двоичном виде число j).

Функция эта нелинейна, немонотонна и несамодвойственна и согласно теореме об ослабленной функциональной полноте позволяет при использовании булевых констант 1 и 0 путем суперпозиций реализовать любую булеву функцию  [15].

Синтез комбинационных схем на мультиплексорах удобно осуществлять с помощью теоремы разложения [15]. Эта теорема позволяет любую булеву функцию F (х_п-\, х_п~2, ..., х\_у хо) раз­ложить по i переменным Xn-i,x_n-2, . >., x_n-i и представить как

где Rj — конъюнкция, равная 1 на наборе значений перемен­ных х„-1, х_п-2, ..., ^xn~i с номером /, а Я — функция, получен­ная из F подстановкой в нее набора значений переменных х_п-\,Хп-2, ••♦, Xn-i с номером /.

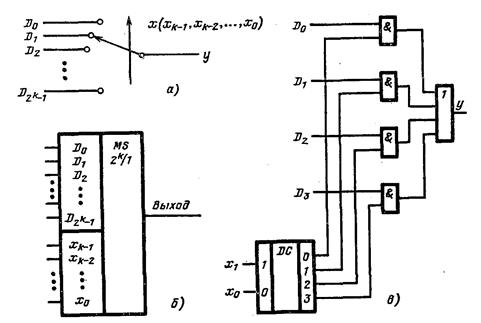
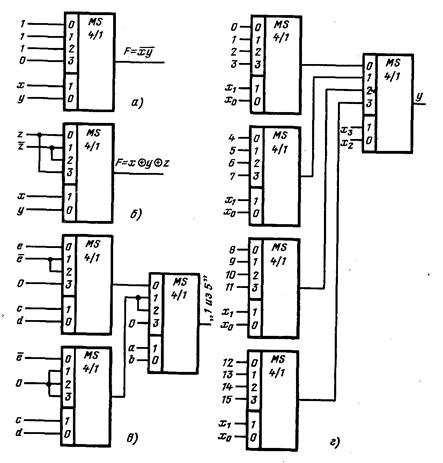
Рис. 3.21. Схемы из мультиплексоров:

а — И — НЕ; 6 — сложение по модулю 2; в ~ двухкаскадное мультиплексиро­вание; г — многокаскадный мультиплексор

Сравнивая (3.9) и (ЗЛО), легко заметить, что на основе разложения булевой функции F по к переменным можно строить реализующую ее схему на мультиплексорах. Для этого необхо­димо подать на входы мультиплексора D₀₎ D_u ..., D _k сиг­налы, представляющие функции разложения F°_t F^l, а на управ­ляющие входы — сигналы к переменных, по которым выпол­нялось разложение. Если функция F имеет п = к аргументов, то функции разложения F°, F^х... — константы, и на вход D, муль­типлексора подается константа, равная значению F на наборе с номером /\ При числе аргументов функции F, равном (£+1), функции разложения могут иметь вид х, либо х, либо 0, либо

1. Подавая на входы Do, D\... мультиплексора такие сигналы, можно реализовать на одной микросхеме мультиплексора любую функцию k-{-\ переменной. Если п>к-{-\_у то функции разложе­ния могут зависеть от нескольких переменных и для реализации их потребуются схемы, которые можно построить, разложив -функции разложения так же, как и исходную по к переменным, и т. д.

На рис. 3.21 даны примеры построенных ^%на мультиплек­сорах схем, реализующих функции И — НЕ, сложения по моду­лю 2 и функцию выделения наборов пяти переменных, содержа­щих одну 1.

Корпус (кристалл) микросхемы может содержать несколько мультиплексорных схем. Выход мультиплексора может быть как прямым, так и инверсным по отношению к сигналам D_o, D\...; мультиплексор может быть снабжен входом выборки (синхрони­зации). Число управляющих входов у микросхем мультиплексо­ров обычно находится в пределе 1—4. При необходимости по­строения мультиплексоров с большим числом входов строятся каскадные схемы. Пример такой схемы дан на рис. 3.21, г.