Форматы данных для персональных ЭВМ

Билет 6,7

Форматы данных для ПЭВМ.

Форматом числа называют представление числа в разрядной сетке ЦВМ с соблюдением определенных правил, таких как обозначение знака, размещение целой и дробной частей.

Рис. 1.1. Разрядная сетка 16-тиразрядной ЦВМ

В зависимости от размещения целой и дробной частей числа без учета размещения знака различают следующие форматы или формы представления чисел в ЦВМ:

- естественную, или с фиксированной запятой;

- нормальную, или с плавающей запятой, которую называют также полулогарифмической.

Естественная форма представления чисел нашла достаточно широкое применение в специализированных ЦВМ (бортовых, управляющих технологическими процессами), а также в вычислителях различных измерительных и управляющих устройств.

Числа с фиксированной запятой. При представлении чисел в форме с фиксированной запятой, положение последней фиксируется в определенном месте относительно разрядов числа и сохраняется неизменным при всех вычислениях.

Количество разрядов, отводимое для целой и дробной частей, устанавливают при конструировании машины. Обычно подразумевается, что запятая располагается или перед старшим разрядом (так принято в некоторых специализированных ЦВМ), или после младшего.

В первом случае - это дробные числа меньше единицы, а во втором - целые числа.

Шестнадцатиразрядная сетка специализированных ЦВМ (формат числа) изображена на рис.1.2. Разряд, стоящий слева от запятой, определяет знак числа и называется знаковым.

Рис.1.2. Формат числа с фиксированной запятой

Знаку "плюс" соответствует нуль в знаковом разряде, а знаку "минус" - единица. Например, последовательность  0,01011 является машинным изображением положительного числа, а последовательность  1,01011  - отрицательного.

На рис.1.2 изображено размещение двоичного числа   в разрядной сетке. Знаковый разряд хранится в 15-м разряде, старший разряд мантиссы числа  в 14-м, младший разряд мантиссы  в нулевом разряде.

Количество разрядов в разрядной сетке ЦВМ полностью определяет диапазон и точность представления чисел. Максимальное машинное число меньше единицы и с фиксированной запятой, которое может быть представлено в -разрядной ЦВМ без учета знака определяется выражением

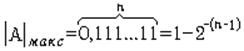                                 (1.15)

а минимальное - выражением

                                      (1.16)

Следовательно, диапазон  чисел  представляемых  в ЦВМ в естественной форме определяется неравенством

                                                (1.17)

или

                                          (1.18)

В ЦВМ, оперирующей числами, представленными в форме с фиксированной запятой, числа большие по величине, чем  не могут быть представлены, так как требуют дополнительных разрядов слева от предполагаемой  запятой. Если число выходит за верхний предел неравенства (1.17), то целая часть числа теряется, что приводит к искажению величины числа. Происходит, так называемое, переполнение разрядной сетки слева. В целях предотвращения этого проводится масштабирование чисел.

Масштабирование осуществляется введением масштабных коэффициентов, которые выбираются таким образом, чтобы для вводимых чисел и чисел, получаемых в процессе вычислений, выполнялось условие (1.17).

Масштабный коэффициент  связывает реальное (истинное)  число  и  его машинное изображение (код) соотношением

                                                    (1.19)

Числа меньшие, чем , также не могут быть представлены в ЦВМ, так как они требуют дополнительных разрядов правее младшего машинного разряда. Происходит, так называемое, исчезновение порядка. Появляются машинные нули, т.е. числа не равные в действительности нулю, но изображаемые в машине нулем из-за нехватки разрядов справа.

Ранее отмечалось, что в общем случае двоичное число  в форме с фиксированной запятой записывается в виде

                     ,                      (1.20)

а его абсолютное значение

                                             (1.21)

Так как знаковый разряд числа является самым левым в разрядной сетке, то любое число такой ЦВМ можно формально изменять на величину ,  и т.д. (на величину кратную  ), т.е. справедливо выражение

                                                      (1.22)

Например,

но ввиду ограниченности разрядной сетки слева единица старшего разряда теряется и результат сложения равен 0,11011.

Также справедливы выражения: ,

 и т.д.

Числа с плавающей запятой. Эта форма представления чисел является основной для ЦВМ серии ЕС ЭВМ, серии СМ и персональных компьютеров.

При представлении чисел в форме с плавающей запятой, число записывается в разрядную сетку ЦВМ в виде двух групп цифр  (рис.1.3). Одна группа цифр обозначает порядок числа, а другая - мантиссу.

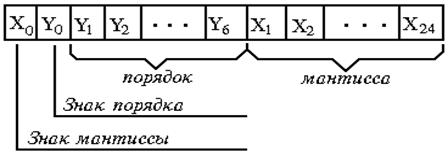
Рис.1.3. Формат числа с плавающей запятой

Для изображения чисел с плавающей запятой используется выражение

                                                           (1.23)

где - основание системы счисления;  - порядок числа (целое число);  - мантисса числа (дробное число).

Часть числа  называют характеристикой. Она выражена в логарифмической форме, поэтому такое представление числа называют полулогарифмическим. Значение  со знаком указывает истинное положение запятой в числе .

Для ЦВМ, использующих двоичную систему счисления,  выражение (1.23) принимает вид

                                                        (1.24)

Рассмотрим четыре различных положительных числа с одинаковыми мантиссами, представленных в форме с плавающей запятой.

В левой части приведенных равенств стоят истинные значения чисел в двоичном коде, а в правой части - их представления в форме с плавающей запятой. Из правых частей равенств видно, что числа имеют одинаковые мантиссы, но вследствие различных порядков для этих чисел, положение запятой в них различно. Таким образом, с помощью задания порядка можно изменить истинное положение запятой в числе. Отсюда  и  название "плавающая запятая".

Обычно ЦВМ, использующие числа в форме с плавающей запятой, оперируют с, так называемыми, нормализованными числами, т.е. числами у которых в старшем разряде мантиссы стоит единица. Поскольку первому разряду после запятой соответствует величина , то для мантиссы нормализованного числа справедливо неравенство

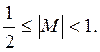                                                         (1.25)

Рассмотрим две записи числа 41,75 в двоичной системе счисления в форме с плавающей запятой

Пусть для мантиссы в машине отведено восемь разрядов. Тогда мантисса первой записи числа полностью разместится в этих разрядах, в то время как в мантиссе второй записи будут потеряны две единицы младших разрядов.

Первая запись относится к нормализованному числу, вторая - к ненормализованному. Из сравнения двух записей одного числа следует, что использование нормализованных чисел увеличивает точность вычислений, так как разряды, отведенные для мантиссы числа, используются полностью.

Операция приведения числа к нормализованному виду называется нормализацией. Нормализация осуществляется сдвигом мантиссы с соответствующим изменением порядка числа.