Составление логической функции для цифровых схем, представленных таблицей истинности

Билет № 12

Составление логической функции для цифровых схем, представленных таблицей истинности.

Логические выражения функций могут быть представлены в двух основных формах:

1. сумма произведений -

2. произведение сумм -

Булевое выражение в виде суммы произведений в технической литературе называют дизъюнктивной нормальной формой  (ДНФ).

А булевое выражение в виде произведения сумм называют конъюнктивной нормальной формой (КНФ).

Если в состав логической формулы входят наборы элементарных конъюнкций одинакового ранга, связанные дизъюнкцией, то такая форма представления логической функции получила название совершенной дизъюнктивной нормальной формы (СДНФ)

.

Функция  отвечает требованиям к СДНФ, так как:

а) в ней нет двух одинаковых конъюнкций;

б) ни одна конъюнкция не содержит двух одинаковых двоичных переменных;

в) никакая конъюнкция не содержит двоичную переменную вместе с ее отрицанием;

г) все конъюнкции  одного ранга.

Конъюнкции одинакового ранга, состоящие из одних и тех же переменных, называются соседними, если они отличаются инвертированием только одной переменной. Примером соседних конъюнкций являются элементарные конъюнкции

Соседние конъюнкции можно объединить, вынося за скобки повторяющиеся логические выражения. Это объединение соседних конъюнкций получило название метода склеивания и используется для понижения ранга конъюнкции в СДНФ. Если функция содержит конъюнкции разных рангов, то следует использовать следствие  для конъюнкции младшего ранга и повысить ранг конъюнкции для образования СДНФ функции . Например,

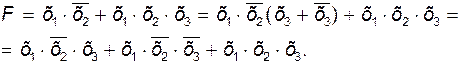
Совершенной конъюнктивной нормальной формой (СКНФ) логической функции принято называть такое ее выражение, которое содержит элементарные дизъюнкции одного ранга, связанные конъюнкцией

Функция  отвечает следующим условиям:

а) в ней нет двух одинаковых элементарных дизъюнкций;

б) ни одна дизъюнкция не содержит двух одинаковых двоичных аргументов;

в) ни одна дизъюнкция не содержит переменную вместе с ее отрицанием;

г) все дизъюнкции одного ранга.

Булево выражение - это удобный метод описания принципа  работы логической схемы реализующей переключательную функцию.

Таблица истинности - это другой точный метод описания того, как работает логическая схема.

Необходимо уметь преобразовывать информацию, представленную в форме таблицы истинности в булево выражение.

Приведем порядок перехода от табличного задания логической функции к аналитическому в дизъюнктивной (конъюнктивной) форме:

1. Составить логические произведения (суммы) переменных для строк таблицы истинности, в которых функция равна единице (нулю). Если значение переменной в строке равно нулю (единице), то в произведении (сумме) записывается отрицание этой переменной.

2. Написать логическую сумму (произведение) составленных произведений (сумм).

Например, пусть исследуемая логическая функция , трех переменных задана таблицей истинности, представленной в табл. 1.7.

Для составления СДНФ используем вторую, третью, пятую и восьмую строки таблицы истинности.

Для второй строки можно записать, что  при    т.е. .

                                              Таблица 1.7

Таблица истинности логической функции трех аргументов

№ строки
1	0	0	0	0
2	0	0	1	1
3	0	1	0	1
4	0	1	1	0
5	1	0	0	1
6	1	0	1	0
7	1	1	0	0
8	1	1	1	1

Аналогично, для третьей, пятой и восьмой строк запишем

, ,

Написав логическую сумму составленных конъюнкций, по-лучим аналитическое выражение, связывающее все наборы переменных, заданные таблицей истинности, при которых , в СДНФ

 

Для получения СКНФ используем первую, четвертую, шес-тую и седьмую строки табл. 1.7.

Для первой строки можно записать, что  если    т.е. .

Аналогично, для четвертой, шестой и седьмой строк запишем

, ,

Написав логическую сумму составленных конъюнкций, получим аналитическое выражение, связывающее все наборы переменных,  заданные таблицей истинности, при которых , в СДНФ

 

Применим операцию отрицания к левой и правой части  полученного равенства:

или на основании закона двойного отрицания и правила де- Моргана

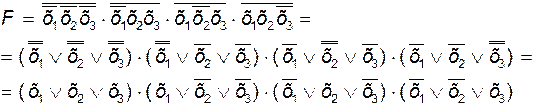
Последнее выражение можно записать сразу в соответст-вии с выше изложенным порядком перехода от табличного за-дания логической функции к аналитическому в конъюнктив-ной форме: 

Графический способ описания логических функций основан на использовании условных обозначений двоичных логических элементов по ГОСТ 2.743-72, каждая логическая функ-ция обозначается прямоугольником, который содержит основ-ное и, при необходимости, дополнительные поля. Двоичные переменные являются входами, а функция - выходом. Входы всегда располагаются слева, а выходы - справа.