Основы аппроксимации функциональных зависимостей

Лекция 3

Основы аппроксимации функциональных зависимостей

1.  Базовые положения теории приближения функций и классификация методов аппроксимации.

На практике не всегда представляется возможным представить связь величины (в общем случае) с величиной  (аргументом) в виде некоторой явно выраженной аналитической зависимости . В тех же случаях, когда это возможно, данная зависимость может быть настолько сложной (например, содержать трудно вычислимые выражения, интегралы и т.д.), что её использование в практических расчетах затруднительно.

            Наиболее распространенным и практически важным случаем, когда вид связи между параметрами и неизвестен, является задание этой связи в виде некоторой таблицы пар значений {,} (i=1,...,n). Этими значениями могут быть либо результаты расчетов, либо экспериментальные данные (т.е. данные, полученные в результате натурного либо математического эксперимента или моделирования).

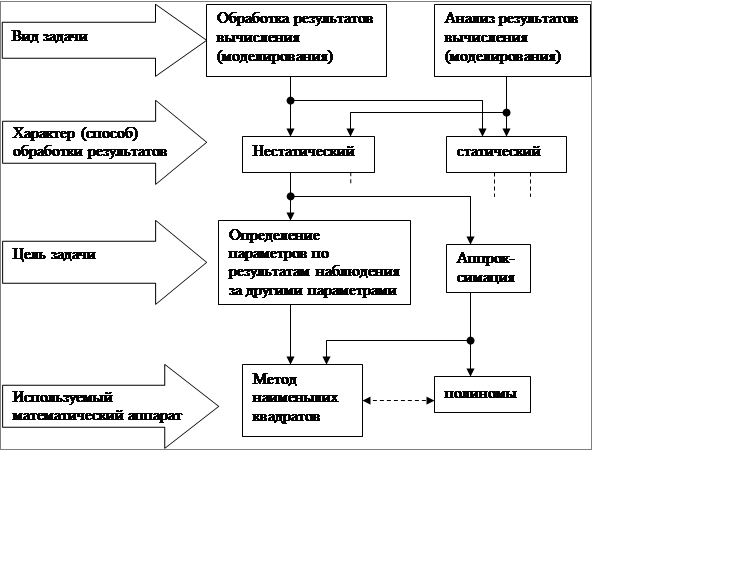
Рис.1  Место аппроксимации при решении

инженерных и исследовательских задач

На практике часто может возникать необходимость знания значений функции  в других точках, отличных от известных значений аргумента . Такая необходимость может иметь место, например, при проведении исследования поведения некоторой системы в моменты времени , находящиеся между значениями и . В свою очередь невозможность получения значений  обусловлена чаще всего жёсткими условиями на время проведения эксперимента, связанными, в свою очередь с необходимостью получения большого статического материала (именно в точках ()  )  с целью удовлетворения требованиям точности и достоверности результатов эксперимента.

            Задача определения значений  решается с помощью аппроксимации – замены функции некоторой приближенной функцией  таким образом, чтобы отклонение (по некоторому критерию)  от  было наименьшим в заданной области значений аргумента.

            Для практики весьма важным является аппроксимация функций  многочленом , коэффициенты  которого подбираются так, чтобы достигалось наименьшее отклонение значений  от  .

            Классификационная схема видов аппроксимации представлена на рис.1.

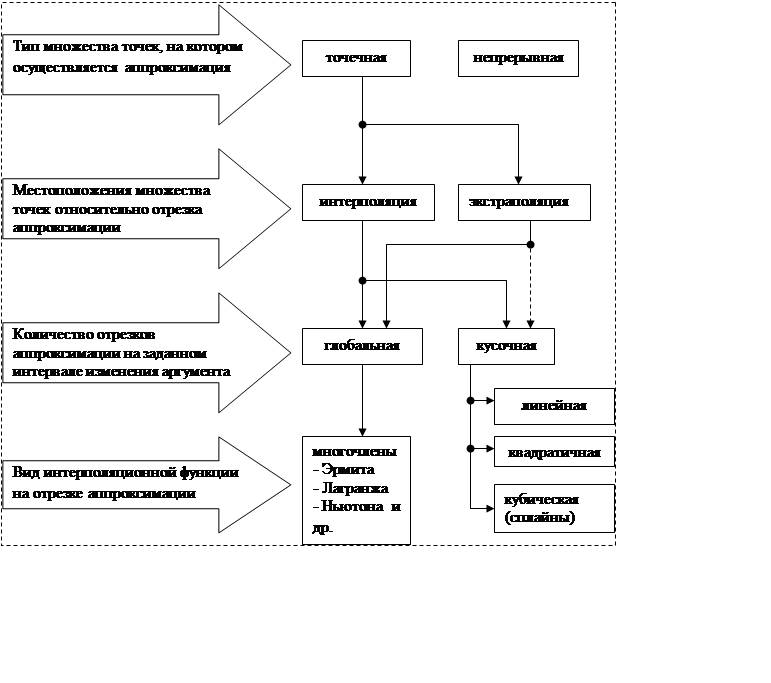
Основным типом точечной аппроксимации является интерполяция, состоящая в следующем: для данной функции  строится многочлен,  принимающий в заданных точках  те же значения , что и функция , т.е. . При этом предполагается, что среди значений  нет одинаковых, т.е.  при . Точки  называются узлами интерполяции, а многочлен  - интерполяционным многочленом. Таким образом, близость интерполяционного многочлена и заданной функции состоит в том, что их значения совпадают на заданной системе точек.

Максимальная степень интерполяционного многочлена ; в этом случае имеет место глобальная интерполяция, поскольку один многочлен  используется для интерполяции функции  на всём интервале измерения х.

В случае глобальной интерполяции при большом числе узлов интерполяции получается высокая степень интерполяционного многочлена.

Следует, однако, отметить, что построение аппроксимирующего многочлена с обязательным выполнением условия прохождения через узлы интерполяции  может означать повторение допущенных в ходе эксперимента ошибок, если такие ошибки имели место. Выход из этого положения может быть найден выбором такого многочлена, график которого проходит близко от данных точек .

Следует отметить, что могут существовать различные критерии «близости» интерполяционного многочлена по отношению к точкам .

Одним из наиболее распространённых видов приближения является