x=sin(2*pi*335*t);
plot(t,x)
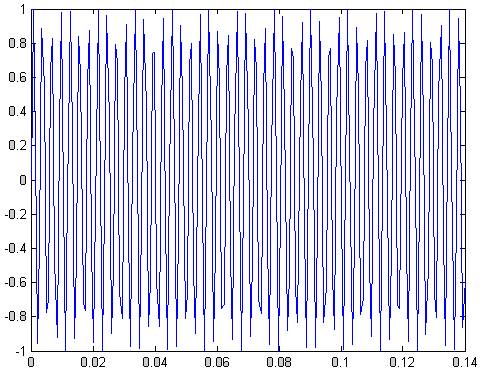
Рис.64 синусоидальный сигнал в зоне пропускания
x1=ifft(x,201);
x1=x1/0.0007;
plot(t,real(x1))
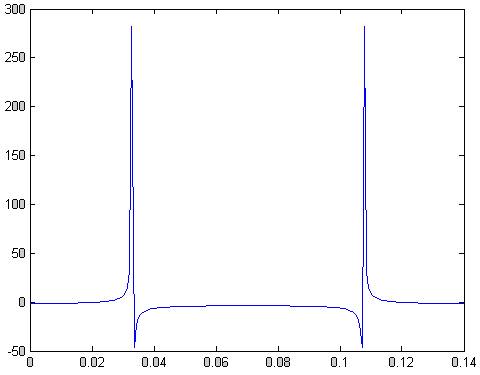
Рис.65 реальная часть
plot(t,imag(x1))
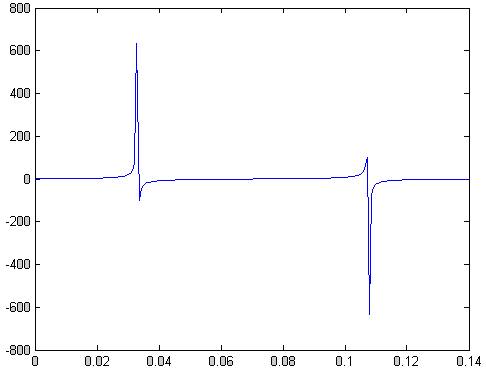
Рис.66 мнимая часть
x=sin(2*pi*455*t);
plot(t,x)
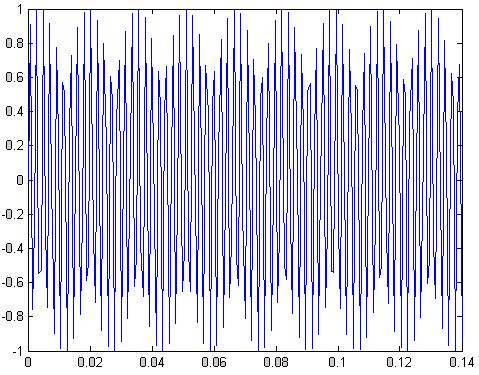
Рис.67 синусоидальный сигнал в зоне задерживания
x1=ifft(x,201);
x1=x1/0.0007;
plot(t,real(x1))
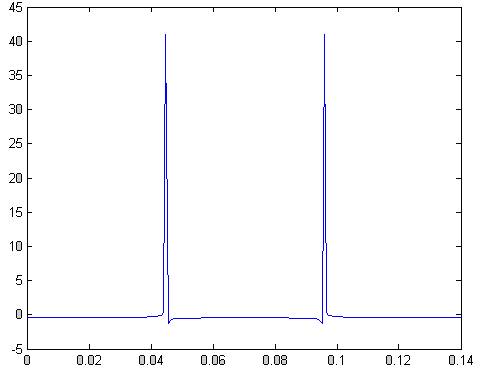
Рис.68 реальная часть
plot(t,imag(x1))
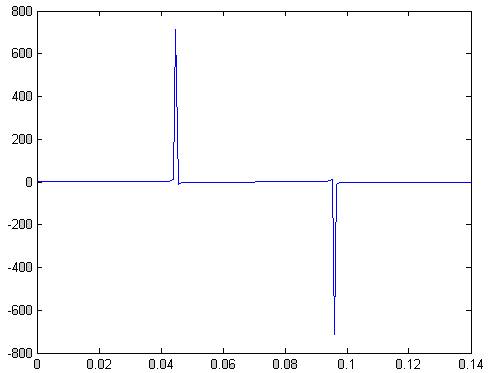
Рис.69 мнимая часть
Реакцмя на бигармонический импульс
x=sin(2*pi*335*t)+sin(2*pi*455*t);
plot(t,x)
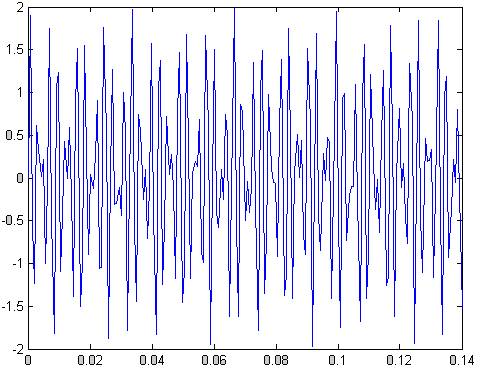
Рис.70 бигармонический сигнал
x1=ifft(x,201);
x1=x1/0.0007;
plot(t,real(x1))
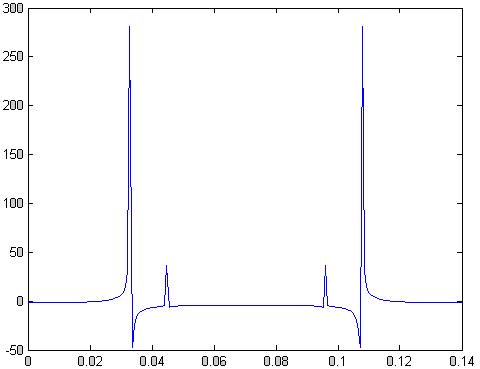
Рис.71 реальная часть
plot(t,imag(x1))
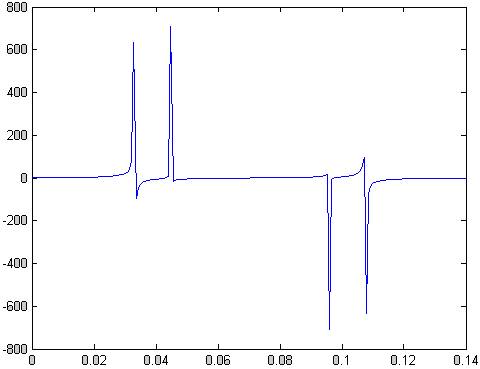
Рис.72 мнимая часть
3 Использование весовых окон при ДПФ.
Моделируем сигнал:
x=sin(2*pi*240.4*t)+sin(2*pi*489.5*t);
plot(t,x)
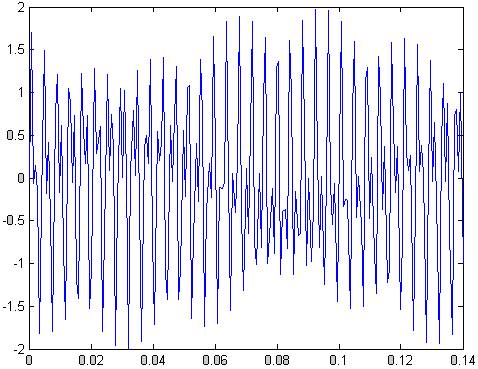
Рис.73 сумма двух синусоид
plot(f,abs(xf(1:101)))
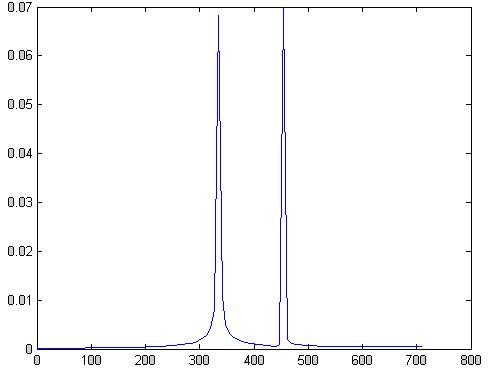
Рис.74 АЧХ
Весовое окно Бартлета
w=bartlett(201);
x=x';
x1=x.*w;
plot(f,abs(x1(1:101)))
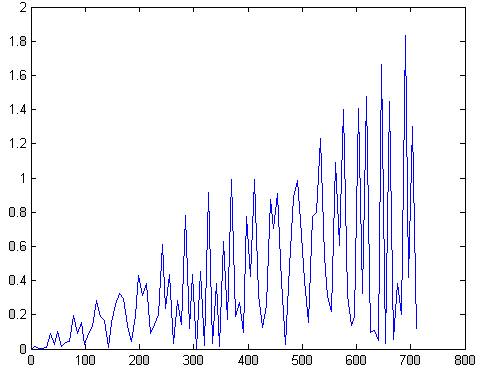
Рис.75 АЧХ сигнала умноженное на окно Барлетта
Весовое окно Блэкменса
w=blackman(201);
x1=x.*w;
plot(f,abs(x1(1:101)))
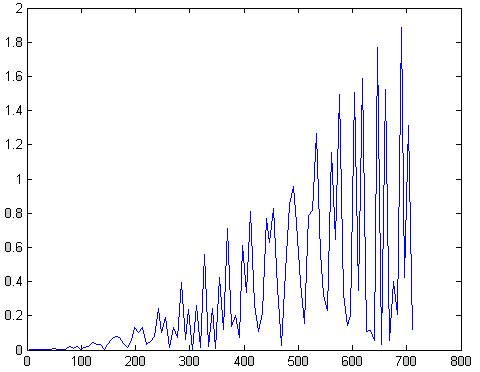
Рис.76 АЧХ сигнала умноженное на окно Блэкменса
Весовое окно Хамминга
w=hamming(201);
x1=x.*w;
plot(f,abs(x1(1:101)))
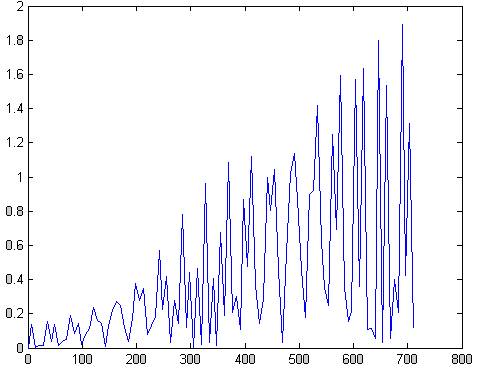
Рис.77 АЧХ сигнала умноженное на окно Хамминга
Весовое окно Ханна
w=hann(201);
x1=x.*w;
plot(f,abs(x1(1:101)))
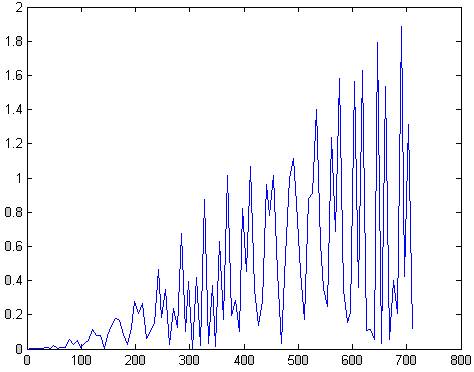
Рис.78 АЧХ сигнала умноженное на окно Ханна
Весовое окно Тьюки
w=tukeywin(201,0.5);
x1=x.*w;
plot(f,abs(x1(1:101)))
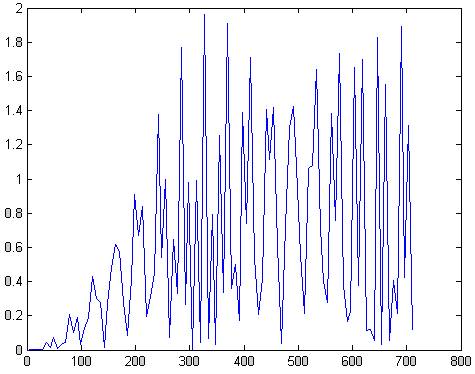
Рис.79 АЧХ сигнала умноженное на окно Тьюки
4 Наложение частот при использовании дискретного преобразования Фурье.
x=sin(2*pi*350*t)+sin(2*pi*875*t);
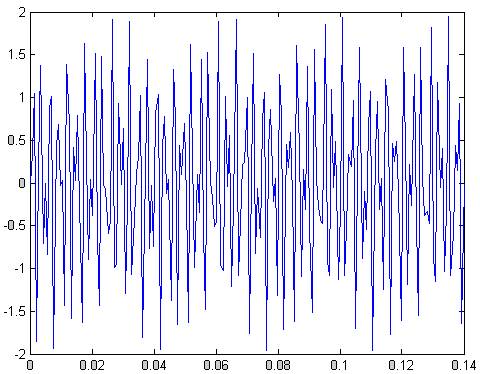
Рис.80 сумма двух синусоид
plot(f,abs(x(1:101)))

Рис.81 АЧХ смоделированного сигнала
Уменьшаем шаг квантования в два раза
t=0:0.00035:0.28;
x=sin(2*pi*350*t)+sin(2*pi*875*t);
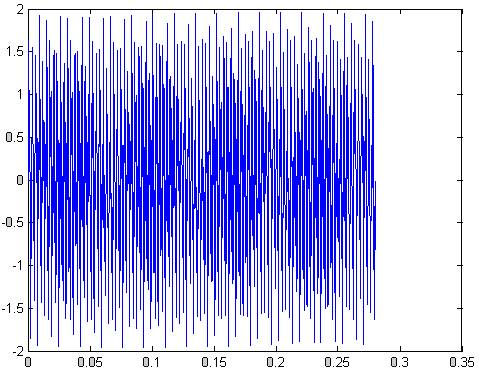
Рис.82 смоделированный сигнал
plot(f,abs(x(1:101)))
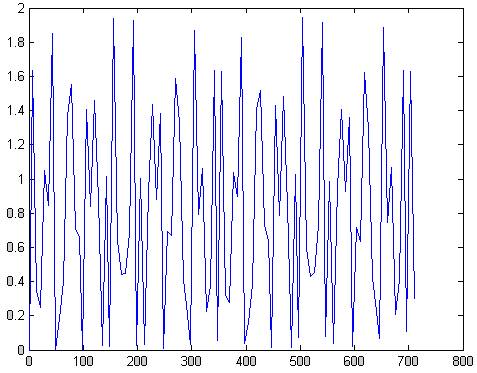
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.