</A></Q1><Q1 10> Вид функции, описывающей прозрачность энергетического барьера
<A 0> Гиперболический.
</A><A 0> Параболический.
</A><A 0> Полином.
</A><A 1> Экспонента.
</A><A 0> Синусоида.
</A></Q1><Q1 10> Как соотносятся точности нахождения неопределённостей координат и импульса микрочастицы?
<A 0> Точность определения координаты выше.
</A><A 0> Точность определения импульса выше.
</A><A 0> Нельзя найти с высокой точностью ни то, ни другое.
</A><A 1> По отдельности каждую из величин можно найти с какой угодно точностью.
</A><A 0> Это зависит от величины энергии и массы частицы.
</A></Q1><Q1 10> Туннельный эффект основывается на:
<A 1> Свойстве частиц с полной энергией, меньше, чем высота барьера, этот барьер с некоторой вероятностью преодолевать.
</A><A 0> Особенностях нахождения частицы в бесконечно глубокой яме с тонкими стенками.
</A><A 0> Принципе сверхпроводимости.
</A><A 0> Нерелятивистском подходе к излучению свойства преодоления частицами потенциальных барьеров.
</A><A 0> Следствии из второго уравнения Максвелла.
</A></Q1><Q1 10> Для описания состояния частицы в одномерной прямоугольной яме с бесконечно высокими стенками применяют
<A 0> Закон Стефана-Больцмана.
</A><A 1> Уравнение Шредингера
</A><A 0> Соотношение неопределённости Гейзенберга.
</A><A 0> Уравнение Бернулли.
</A><A 0> Второй закон Ньютона.
</A></Q1><Q1 10> Если в
уравнении Шредингера 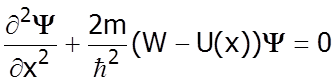 y-функция
имеет вероятностный смысл, и y(0)=0, y(l)=?:(для бесконечно глубокой ямы)
y-функция
имеет вероятностный смысл, и y(0)=0, y(l)=?:(для бесконечно глубокой ямы)
<A 0> 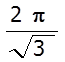
</A><A 0> 1
</A><A 0> 7,423
</A><A 1> 0
</A><A 0> -23,75+7.6j
</A></Q1><Q1 10> Что есть n
в уравнении 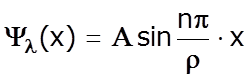 (уровень энергии)?
(уровень энергии)?
<A 0> Порядок уровня.
</A><A 1> Главное квантовое число.
</A><A 0> Степень свободы элемента.
</A><A 0> Коэффициент упругости.
</A><A 0> Заряд ядра элемента.
</A></Q1><Q1 10> Что
описывает функция ![]()
<A 0> Вероятность обнаружения частицы за потенциальным барьером.
</A><A 0> Плотность вероятности обнаружения частицы за потенциальным барьером.
</A><A 1> Свободное состояние частицы.
</A><A 0> Колебательный процесс в газе.
</A><A 0>
Колебательный процесс при условии наличия силы, не превышашающей по модулю ![]() ,
,
</A></Q1><Q1 10> Какова вероятность обнаружения частицы, полная энергия которой ни в один момент времени не превышает высоты потенциального барьера, за этим самым барьером?
<A 0>Нулевая.
</A><A 0>Полная.
</A><A 1> Ненулевая, но стремится к нулю.
</A><A 0> Стремится к нулю.
</A><A 0> Варьируется от нуля к единицы.
</A></Q1><Q1 10> Частица устойчиво существует лишь в таком элементарном состояниии, в таком ящике, когда:
<A 0> Её состояние можно описать уравнением Шредингера.
</A><A 0> Дает сплошной спектр.
</A><A 0> Обладает сплошной спектр.
</A><A 1> Образует стоячую волну де Бройля.
</A><A 0> Движется со скоростью света.
</A></Q1><Q1 10> Туннельный эффект основывается на :
<A 1> свойстве частиц с полной энергией меньшей энергии барьера, этот барьер с некоторой вероятностью преодолевать.
</A><A 0> особенностях нахождения частицы в бесконечно глубокой яме с тонкими стенками.
</A><A 0> принципе сверхпроводимости.
</A><A 0> нерелятивистком подходе к изучению свойств преодоления частицами потенциального барьера.
</A><A 0> следствие из второго уравнения Максвелла.
</A></Q1>
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.