Текущее
время t до середины первого участка ![]() мин
мин
до середины второго участка ![]() мин
мин
до середины третьего участка ![]() мин
мин
до середины четвертого участка ![]() мин
мин
Проекции наклонных участков на ось ординат (высота ступенек):
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Нормальная амплитудно – фазовая характеристика:
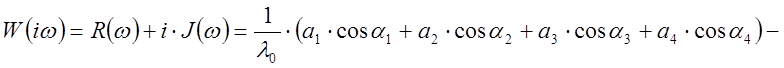
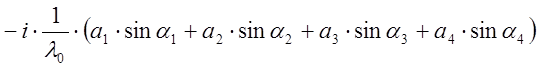
где
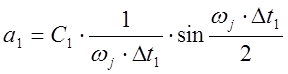 ,
, ![]()
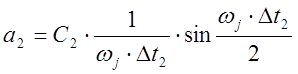 ,
, ![]()
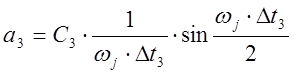 ,
, ![]()
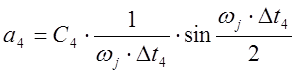 ,
, ![]()
Все вычисления сведем в табл. П3. Расчеты приведены для частот w=0,001; 0,002; 0,004; 0,008 рад/с.
Табл. П3
|
Наименование величин |
w=0,001 |
w=0,002 |
w=0,004 |
w=0,008 |
|
|
0.06 |
0.12 |
0.24 |
0.48 |
|
|
0.21 |
0.42 |
0.84 |
1.68 |
|
|
0.45 |
0.9 |
1.8 |
3.6 |
|
|
0.84 |
1.68 |
3.36 |
6.72 |
|
|
16.67 |
8.33 |
4.17 |
2.08 |
|
|
11.11 |
5.56 |
2.78 |
1.39 |
|
|
6.67 |
3.33 |
1.67 |
0.83 |
|
|
4.17 |
2.08 |
1.04 |
0.52 |
|
|
0.06 |
0.12 |
0.238 |
0.462 |
|
|
0.208 |
0.408 |
0.475 |
0.994 |
|
|
0.435 |
0.783 |
0.974 |
-0.443 |
|
|
0.745 |
0.994 |
-0.217 |
0.423 |
|
|
0.998 |
0.993 |
0.971 |
0.887 |
|
|
0.978 |
0.913 |
0.667 |
-0.109 |
|
|
0.9 |
0.622 |
-0.227 |
-0.897 |
|
|
0.667 |
-0.109 |
-0.976 |
0.906 |
|
|
0.06 |
0.12 |
0.24 |
0.48 |
|
|
0.09 |
0.18 |
0.36 |
0.72 |
|
|
0.15 |
0.3 |
0.6 |
1.2 |
|
|
0.24 |
0.48 |
0.96 |
1.92 |
|
|
0.06 |
0.12 |
0.238 |
0.462 |
|
|
0.09 |
0.179 |
0.362 |
0.659 |
|
|
0.149 |
0.296 |
0.565 |
0.932 |
|
|
0.238 |
0.462 |
0.819 |
0.94 |
|
|
0.22 |
0.219 |
0.218 |
0.212 |
|
|
0.19 |
0.189 |
0.186 |
0.174 |
|
|
0.389 |
0.384 |
0.367 |
0.303 |
|
|
0.198 |
0.192 |
0.171 |
0.098 |
|
|
0.219 |
0.218 |
0.212 |
0.188 |
|
|
0.186 |
0.173 |
0.124 |
-0.019 |
|
|
0.35 |
0.239 |
-0.083 |
-0.272 |
|
|
0.132 |
-0.021 |
-0.167 |
0.089 |
|
|
0.887 |
0.608 |
0.086 |
-0.014 |
|
|
0.013 |
0.026 |
0.052 |
0.098 |
|
|
0.04 |
0.077 |
0.138 |
0.173 |
|
|
0.169 |
0.301 |
0.357 |
-0.134 |
|
|
0.148 |
0.191 |
-0.037 |
0.041 |
|
|
0.369 |
0.596 |
0.511 |
0.178 |
По данным таблицы определяем четыре точки амплитудно – фазовой характеристики:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пятая
точка АФХ соответствует ![]() , определяется
непосредственно по кривой разгона:
, определяется
непосредственно по кривой разгона:
![]()
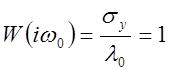
По пяти точкам строится график АФХ в комплексной плоскости (рис. П3)
Рис. П3
3. Аналитический метод расчета устойчивости системы регулирования термической печи.
В зависимости от характера кривой разгона применяют тот или иной линейный закон регулирования.
а) Если объект без самовыравнивания и с запаздыванием, то оптимальный закон регулирования - пропорциональный или пропорционально – дифференциальный:
![]()
б) Если объект с запаздыванием, с самовыравниванием, и малой термической инерцией, то оптимальный закон регулирования - интегральный :
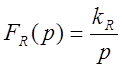
в) Для нашего случая, когда объект с запаздыванием, с самовыравниванием и значительной инерцией, выбирается ПИ – регулятор:
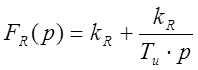
или ПИД – регулятор:
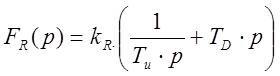
Рассчитаем область устойчивости регулирования температуры полости печи ПИ- регулятором.
Передаточную функцию термической печи в первом приближении рассматриваем как пропорциональное звено с отставанием 1-го порядка – апериодическое звено.
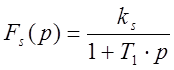
Динамические параметры термической печи:
![]() К/Вт
К/Вт ![]()
Для П – регулятора сигнал на выходе :
![]()
где
отклонение регулируемой температуры ![]() от заданного значения W
равно
от заданного значения W
равно![]()
Передаточная функция:
![]()
Для
И – регулятора 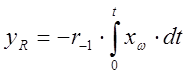 и соответственно передаточная
функция:
и соответственно передаточная
функция:
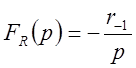 где
где 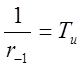
Для выбранного ПИ – регулятора :
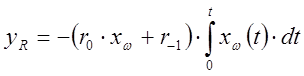
и передаточная функция:
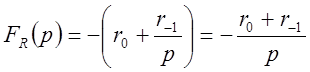 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.