Производство, распределение и использование энергоносителей на промышленном предприятии, страница 3

;

 кДж/кг;

;

 кДж/кг;

;

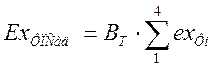 кВт;

 МВт;

Химическая эксергия продуктов сгорания не изменится, поэтому полная эксергия продуктов сгорания составит:

 МВт;

Эксергия золы при адиабатическом горении

;

 кВт;

 МВт;

Эксергия шлака при адиабатическом горении

;

 кВт;

 МВт;

Подставив полученные значения в исходное уравнение, получим:

 МВт;

Потеря эксергия, вызванная необратимой теплопередачей к окружающей среде:

;

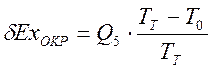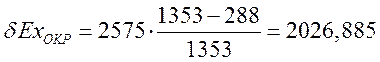 кВт;

 МВт;

Потери эксергии , вызванные внутренним теплообменом в котле и пылесистеме:

;

 МВт.

На основании вычисленных значений  составляем таблицу П3.

Таблица П3

Эксергетический баланс котлоагрегата

Вводимая эксергия				Выход эксергии и потери
№ п/п	В потоке	МВт	%	№ п/п	В потоке	МВт	%
1	Топливо	638,08	100	1	Прирост эксергии рабочего тела	318,59	49,93
				2	Продукты сгорания	21,13	3,31
				3	Зола	0,892	0,14
				4	Шлак	2,08	0,32
				5	Потери от необратимости горения	142,05	22,26
				6	Потери с охлаждением котлоагрегата	2,03	0,32
				7	Потери от внутреннего теплообмена	151,308	23,72
	Итого:	638,08	100		Итого:	638,08	100

Дебаланс: %.

4.  Определение присосов воздуха в газоходе от котлоагрегата к дымососу методом согласования балансов.

При расчете процесса горения получен состав продуктов сгорания на выходе из котлоагрегата:

;

.

Предположим, что через неплотности газохода до дымососа происходит подсос воздуха, и примем величину присоса  м³/м³. Уравнение баланса  при этих условиях:

,     (1)

баланс кислорода :

.     (2)

Используя эти уравнения, можно рассчитать:

;

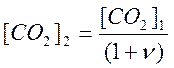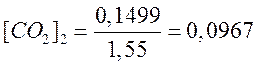, и:

;

.

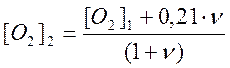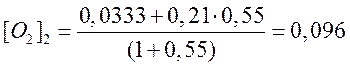Принятое значение  и полученные значения  и  являются истинными.

Если бы ,, и  измерялись в ходе эксперимента, то получены были некоторые приближенные значения. Предположим, что это было бы:

,  ,  ,  .

Обозначим измеренные значения:

;

;
;

.

Определим :

Из уравнения (1):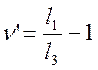

;

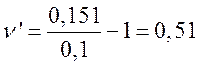Из уравнения (2):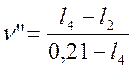

.

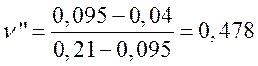Абсолютная погрешность вычисления:

.

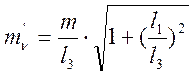Примем ;  - абсолютная погрешность измерения величины .

.

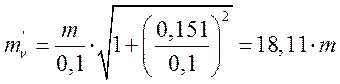Для : ;

.

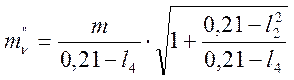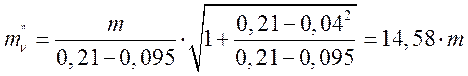Определим несогласование баланса. Основные балансовые уравнения:

;                           (3)

.              (4)

Первый вариант исходных уравнений получим после подстановки в уравнения (3) и (4) значений :

; ,

; .

Второй вариант – после подстановки :

; ,

; .

Для дальнейших расчетов принят вариант I.

Исходная система уравнений:

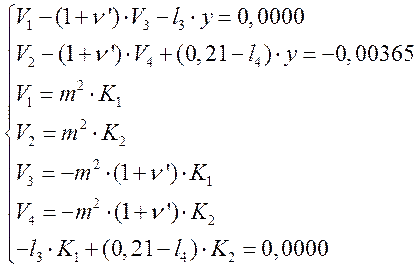
После подстановки численных значений получим:

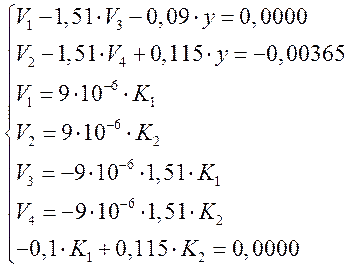
Из уравнения  получим . Тогда:

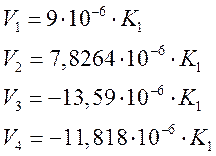
Подставив полученные выражения в первые два уравнения системы, запишем:

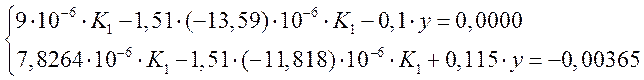
или:

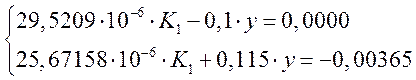
Умножив второе полученное уравнение из системы на  и сложив с первым уравнением получим:

, откуда получим:

.

Подставив полученное значение  в первок уравнение системы, определим :

.

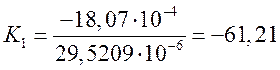Поправки к измеренным величинам:

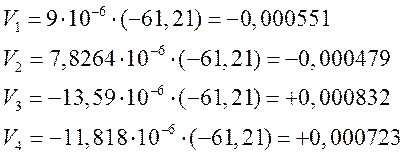
Полученные результаты сведем в таблицу П4.

Таблица П4

Результаты согласования баланса

Величина
Для согласования	0,151	0,04	0,1	0,095	0,51	0,0000	-0,00365
Поправка	-0,000551	-0,000479	0,000832	0,000723	-0,01807
После согласования	0,150449	0,039521	0,100832	0,095723	0,49193
Истинные значения	0,1499	0,0333	0,0967	0,096	0,550

Вывод.

       На основании расчета горения и материального баланса составили баланс энергии и эксергии для парового котла. В балансе эксергии разделили внутренние потери эксергии, учитывая отдельно необратимость горения, потери тепла в окружающую среду и остаточные явления необратимости.

Используя методику согласования баланса, определили присосы воздуха в газоходе парового котла.