Определение режима работы насоса, число оборотов которого = 1450 об/мин. Определение расхода воды через насос, напора насоса, КПД насоса, полезной мощности, затраченной мощности, страница 2

;

При данном расходе на характеристике сети значение напора:

Строим через эту точку  параболу подобных процессов:

                               

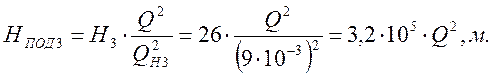
Таблица № 5

Q	0	2	4	6	8	10	12	14	16
HПОД	0	1.3	5.1	11.5	20.5	32.0	46.1	62.7	81.9

Наносим данную параболу на Рис.3.

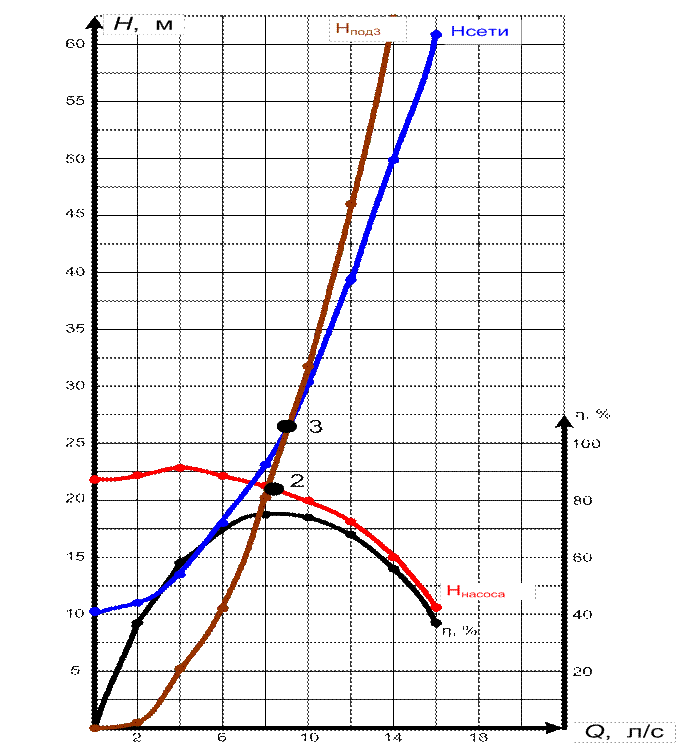
Рис. 3. Характеристика работы насосной станции

Находим точку пересечения параболы подобия и характеристики насоса (точка 2) и определяем расход в этой точке.

Точки 3 и 2 подобны, так как лежат на одной кривой подобия. Используя формулы подобия, найдем частоту оборотов двигателя в новом режиме

.

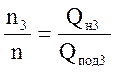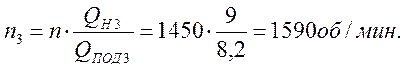
КПД насоса в данном режиме будет находиться с помощью точки 2:

η_н3 = 74%.

Находим полезную мощность насоса:

Определим затраченную мощность, зная полезную мощность и КПД:

;

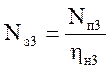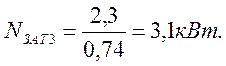
Задача №4

После частичного закрытия крана, при котором коэффициент гидравлического сопротивления φ_кр = 20, определить расход воды, напор, КПД, полезную и затраченную мощности насоса.

Строим характеристику сети при частично открытом кране:

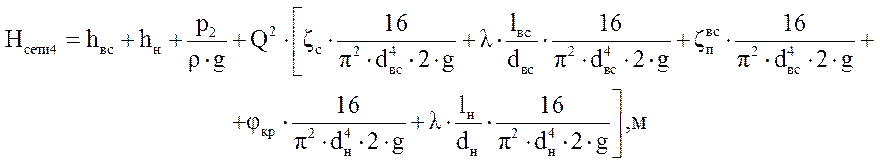
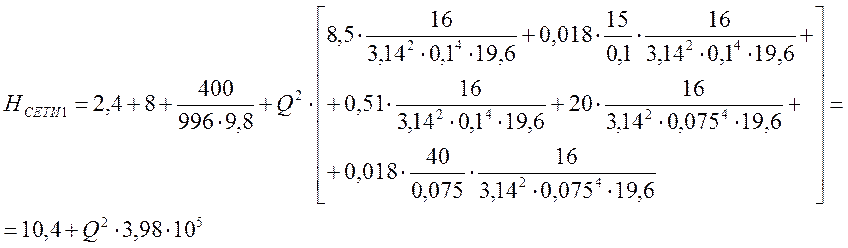
                                                                                                                                   Таблица № 6

Q	0	2	4	6	8	10	12	14	16
HСЕТИ4	10.4	12.0	16.8	24.7	35.9	50.2	67.7	88.4	112.3

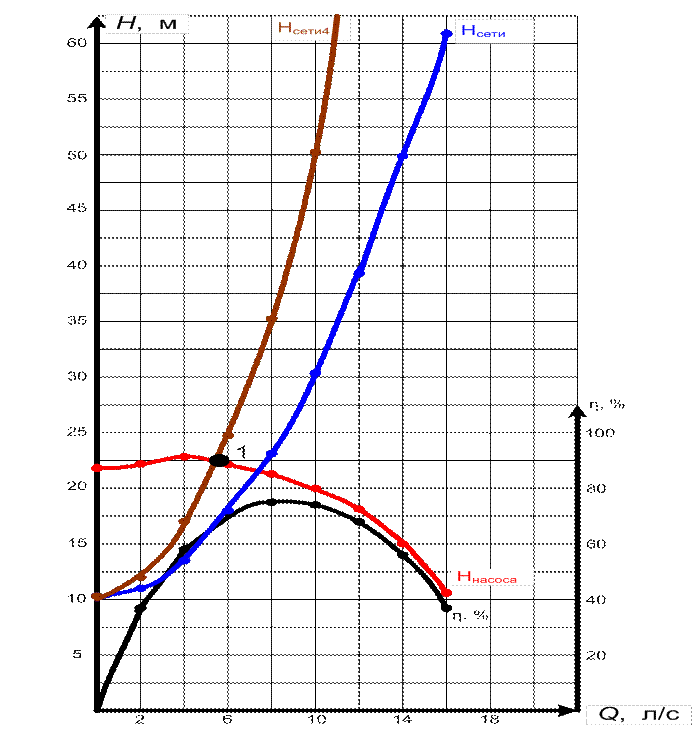
Рис. 4. Характеристика работы насосной станции

Находим точку пересечения характеристик сети и насоса. В этой точке определяем расход, напор и КПД

Q_н4= 5,8 л/с;

H_н4= 22 м;

η_н4= 69 %.

Находим полезную мощность насоса:

Определим затраченную мощность зная полезную мощность и КПД:

;

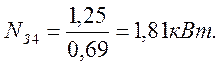
Задача №5

Как надо изменить обороты двигателя, чтобы получить такой же расход, какой получился при частичном закрытии крана, работая на ту же сеть при полном открытии крана. Определить расход воды, напор, КПД, полезную и затраченную мощности насоса.

Берем значение расхода из пункта 4. . При данном расходе найдем точку на характеристике сети  (точка 1) на Рис. 5. и определим напор, соответствующий этому режиму.

Через эту точку строим параболу подобных процессов:

                       

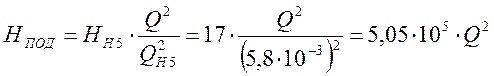
Таблица № 7

Q	0	2	4	6	8	10	12	14	16
HПОД	0	2.0	8.1	18.2	32.3	50.5	72.7	99.0	129.3

Наносим данную параболу на Рис.5.

Находим точку, подобную точке 1 и лежащую на характеристике насоса (точка 2). Расход для этой точки составит:

Из подобия точек 1 и 2 следует формула:

.

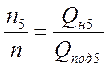Выразим отсюда :                

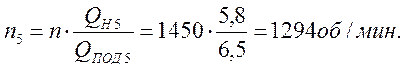
КПД насоса будет находиться при режиме, соответствующем               точке 2 (пересечение абсциссы точки 2 и ):

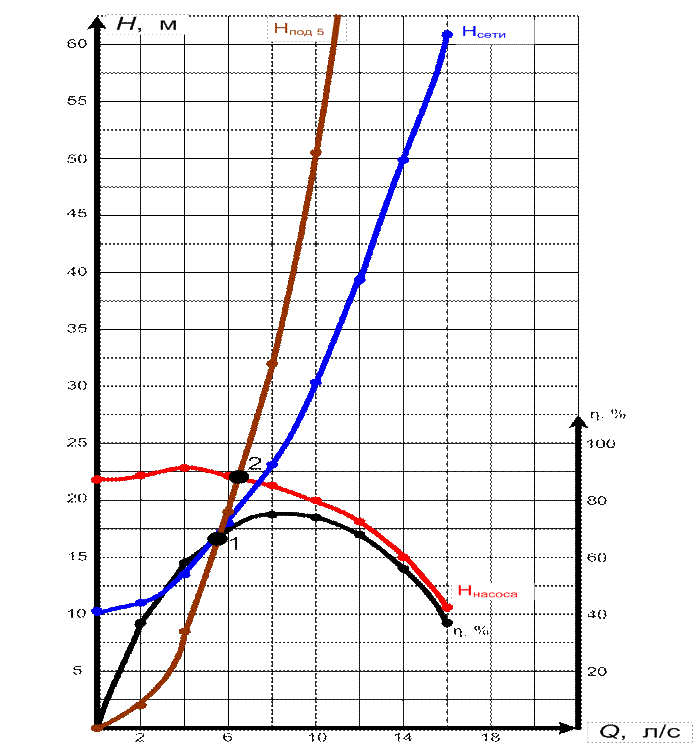
Рис. 5. Характеристика работы насосной станции

Находим полезную мощность насоса:

;

Определим затраченную мощность, зная полезную мощность и КПД:

;

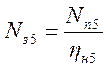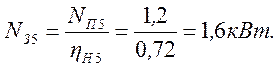
Задача №6

В каком интервале расходов и напоров КПД насоса будет выше 40%, если его скорость вращения уменьшится на α = 20%?

Частота оборотов двигателя при новом режиме:

Так как зависимости H_1(Q) и η_1(Q) нельзя определить однозначно при Q>16 л/с из за недостатка исходных данных, то найдем только одну точку, в которой η₁ = 40%

По характеристике насоса на Рис.1 находим значения напоров и расходов, при которых     η = 40%:

 

Найдем координаты точек, подобных данным двум точкам. Для этого используем формулы подобия:

;

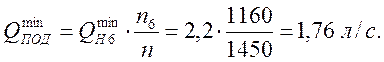
Итак, насос начинает работать с КПД выше 40% при расходе 1,76л/с при напоре 14,37м.