Шифрование информации методом гаммирования и по алгоритму RSA, страница 5

После раскодирования последовательности символов, мы получили исходный текст, что соответствует принципу работы шифрования методом гаммирования.

 Задание №2

Зашифровать фамилию и полное имя студента  по алгоритму RSA.

         Для работы RSA используются простые числа Табл. 5

Табл. 5

Цифра шифра	0	1	2	3	4	5	6	7	8	9
p	7	11	7	11	13	13	5	7	11	5
q	17	19	11	13	17	19	11	13	17	13

     Исходные данные взяты согласно варианту из таблицы 2.1.

p – выбирается по последней цифре шифра.

q – по предпоследней.

p=11

q=17

Решение:

1.     Вычислим произведение порождающих чисел p и q.

2.  Вычислим функцию Эйлера по формуле:

        

         Функция Эйлера показывает количество положительных чисел в интервале от 1 до N, которые взаимно просты с N.

        

3.  Выбираем  (открытый ключ), который должен удовлетворять следующим качествам

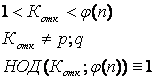
НОД – Наибольший Общий Делитель

4.  Вычислим секретный ключ так, чтобы:

, т. е. обратное число .

Секретный ключ является целым числом по модулю

Вычисление секретного ключа основано на малой теореме Фирма, которую расширил Эйлер.

Формула для вычисления секретного ключа: