








Вариант № 45
Дано:
R1=2 Ом;
R2=2 Ом;
R3=4 Ом;
R4=10 Ом;
R5=10 Ом;
Е1=24 В;
Е2=12 В;
Е3=24 В.
Рис.1-Электрическая схема.
Найти:
1.Определить все токи методом Кирхгофа.
2.Определить токи методом контурных токов.
3.Проверить результаты на баланс токов, напряжений и мощности.
4.Определить один из токов методом эквивалентного генератора.
5.Сделать выводы о проделанной работе
Ход расчета.
1.Определяем токи методом Кирхгофа.
Рис.2- Электрическая схема (метод законов Киргофа)
Число независимых узлов выражается:
ЧНУ= n – 1 = 4 – 1 = 3, где n – общее число узлов цепи.
Число независимых контуров выражается:
ЧНК= q – n + 1 = 6 – 4 +1 = 3, где q- общее число ветвей схемы.
Уравнения составляем для независимых узлов и контуров. Расставим произвольно направления токов в ветвях схемы. Направления обхода конту- ров выберем против часовой стрелки (см. рис. 2).
Составляем уравнения по 1 – му закону Киргофа:
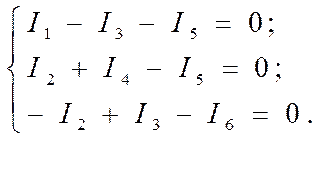
Составляем уравнения по 2 –му закону Киргофа:
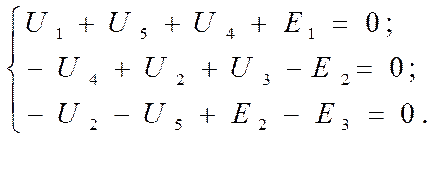
Напряжения на элементах находим по закону Ома:
U1=R1I1, U2=R2I2, U3=R3I3, U4=R4I4, U5=R5I5
Подставив численные значения в данную систему, решаем ее матричным способом и находим токи в ветвях схемы.
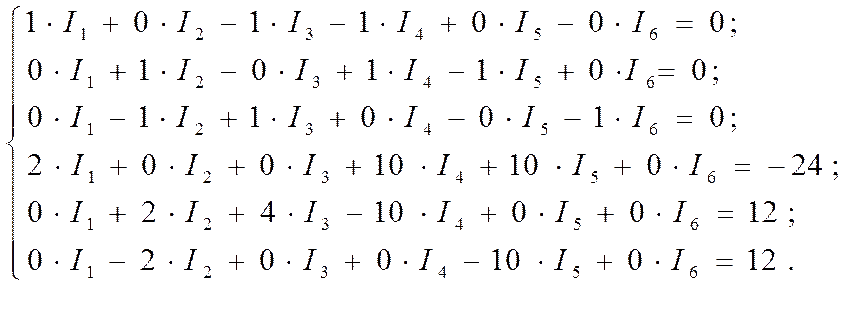
Решая полученную систему уровнений,найдём токи в ветвях системы:
I1 = -0,718A;
I2 = -0,103 A;
I3 = 0,359 A;
I4 = -1,077 A;
I5 = -1,18 A;
I6 = -0,462 A.
2.Определяем токи методом контурных токов.
Рис.3-Электрическая схема (метод контурных токов).
Размечаем стрелки контурных токов J1,, J2, J3. при этом направление стрелок выбираем произвольно. Также произвольно расставим токи в ветвях схемы.
Делая обход контуров против часовой стрелки, получим систему уравнений для контурных токов (см. рис. 3):
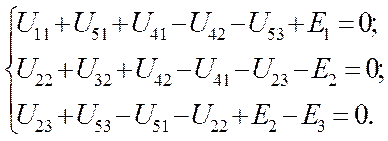
Раскрывая напряжения по закону Ома, получим:
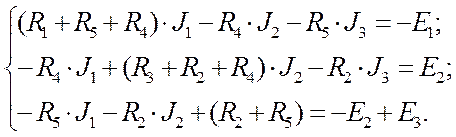
Подставляя числовые значения, получим:
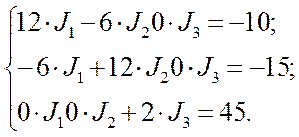
Решая данную систему матричным способом (используя программу МаthCad), находим контурные токи:
J1= -0,718А;
J2= 0,359А;
J3= 0,462А.
Определяем реальные токи в ветвях схемы. Реальные токи смежных, об- щих для двух контуров ветвей определяются как алгебраическая сумма соответствующих контурных токов. Токи в ветвях, входящих в один контур, равны соответствующему контурному току:
I1 = J1 = -0,718А;
I2 = J2-J3= 0,359-0,462= -0,103А;
I3 = J2 = 0,359А;
I4 = J1 - J2 = -0,718-0,359 = -1,077А;
I5 = J1 – J3 = -0,718-0,462= -1,18А;
I6 = J3 = 0,462А.
Если реальный ток получается с отрицательным знаком,то это означает, что ток течёт в направлении, противоположном направлению стрелки на черчеже. При этом ни каких изменений на схеме не делаем, а в дальнейших расчётах используем значение полученного тока с его знаком.
3.Проверка на баланс токов, напряжений и мощности.
а) Проверка на баланс токов.
I1 - I3 – I4 = 0
-0,718-0,359-(-1,077)= 0
0 = 0
I2 + I4 – I5 = 0
-0,103+(-1,077)-(-1,18)= 0
0 = 0
-I2 + I3 - I6 = 0
0,103+0,359-0,462= 0
0 = 0
б) Проверка на баланс напряжений.
![]()
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
U5 = R5 I5 = 10*(-1,18)= -11,8В
U1 + U4 +U5= -E1
-1,436+(-10,77)+(-11,8)= -24
-24 = -24
– U4 +U2+U3 = E2
10,77+(-0,206)+1,436= 12
12 = 12
-U2 –U5= E3 –U2
-(0.206) – (-11.8) = 24- 12
12 = 12
в) Проверка на баланс мощностей.
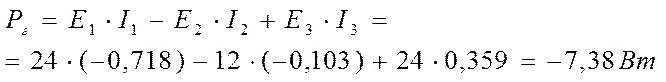 ;
;
![]()
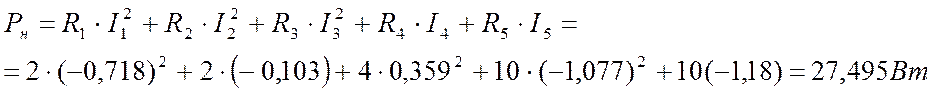 ;
;
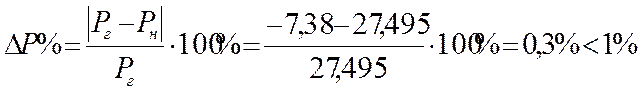
4.Определяем ток в первой ветви методом эквивалентного генератора.
Рис.4-Электрическая схема (метод эквивалентного генератора).
Для этого разомкнем 1-ю ветвь в схеме и найдем напряжение холостого хода (см. рис. 4).
Составим уравнение для контурных токов:
U21+U51-U22+E2-E3=0
U22+U32+U42-U21-E2=0
Раскрывая напряжение по закону Ома, получим:
(R2+R5)*J1-R2*J2= -E2+E3
-R2*J1+(R2+R3+R4)*J2=E2
Подставляя числовые значения, получим:
12J1-2J2=12
-2J1+16J2=12
Решаем данную систему методом Крамера.
Находим главный и побочные определители системы, и находим контурные токи
J1=1,149А
J2=0,894А
Реальные токи в цепи:
I1=J1=1,149
I2=J2=0,894
По второму закону Киргофа находим напряжение холостого хода:
U4+U5+UХХ=0
Откуда:
UХХ =-U4-U5=-I1 R4 –I2 R5= -1,149*10-0,894*10= -20,43В
![]()
Находим входное сопротивление цепи:
Сопротивления R2 и R5 соединены параллельно:
R25= R2*R5\R2+R5=2*10\2+10=1,67 Ом
Получаем следую схему:
Сопротивления R25 и R4 соединены последовательно:
R= R25 + R4 =1,67+10=11,67
Получаем следующую схему:
Находим входное сопротивление:
Rк = R R3\R+R3 = 11,67*4\11,67+4=2,9789 Ом
Находим ток в первой ветви:
I1 = -UХХ –E1\RК+R1=20,43-24\2,9789+2= -0,717026 А
Вывод: при расчёте данной цепи постоянного тока тремя различными методами удалось безошибочно определить искомые токи в ветвях, что подтвердилось результатами проверки и совпадением значений токов при расчёте всеми тремя методами.
Федеральное агенство по образованию
Сибирский государственный технологический университет
Кафедра электротехники
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ
тема: «Расчет цепи постоянного тока»
Выполнил:
cтудент группы 21-01
Кокшаров А.В.
Проверил
преподаватель:
Лурье О.М.
Красноярск 2005
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.