Термодинамическое равновесие носителей заряда, страница 3

Другой фактор, который следует принять во внимание, это то, что электрон в кристалле имеет эффективную массу m^*. Тогда задача сводится к движению электрона с массой m^* вокруг ядра с зарядом Zq в среде с диэлектрической проницаемостью e. В данном случае под Z подразумевается кратность ионизации примесного атома.

Условием устойчивости электрона в классическом понимании будет равенство центробежной и центростремительных сил:

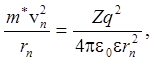                                              (8.1)

где r_n - радиус орбиты; n - номер орбиты.

              В квантовой теории момент количества движения может принимать лишь дискретные значения, кратные постоянной Планка:

                                 (8.2)

Из (8.1) и (8.2) получим

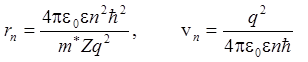.                        (8.3)

Отсюда найдем кинетическую (E) и потенциальную (U) энергию электрона на стационарной орбите:

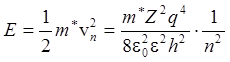,                                (8.4)

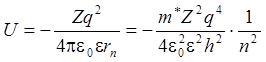.                             (8.5)

Полная энергия связанного электрона равна сумме (8.4) и (8.5)

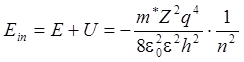 .                              (8.6)

Если принять за начало отсчета энергии дно зоны проводимости E_c = 0, то уровни энергии связанного электрона будут располагаться ниже края зоны проводимости на величину E_in.

              Энергия ионизация примесного атома равна по абсолютной величине E_in при n = 1:

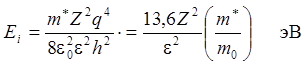.                          (8.7)

Боровский радиус связанного электрона в основном состоянии (n=1), определяется  из   (8.3):

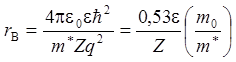        Å .                          (8.8)

Для определения энергии ионизации примесей, образованных элементами V группы в кремнии и германии, которые относятся к непрямозонным полупроводникам, в формуле (8.7) вместо изотропной эффективной массы m^* нужно использовать усредненную комбинацию компонент эффективной массы 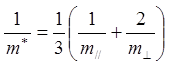, физический смысл которой мы рассмотрим позже.  Из данных табл. 7.1 для Si из получим m^*  = 0,26m₀ и для Ge m^* = 0,12m₀. Значения диэлектрической проницаемости  у кремния e_Si=11,7, а у германия e_Ge=16. Энергия E_i, полученная из (8.7) для кремния имеет величину 25,8 мэВ, а для германия - 6,4 мэВ. Боровский радиус, вычисленный из (8.8) равен 24 Å у Si и 74 Å у Ge.

              Видно, что  в германии  и  кремнии энергия ионизация примесей E_i << E_g. Следовательно, уровни электронов примесных пятивалентных атомов располагаются в запрещенной зоне вблизи дна зоны проводимости. Такие уровни называются мелкими.

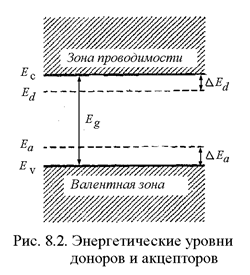
              Согласно водородоподобной модели энергетические уровни электронов трехвалентных примесных атомов также являются мелкими и располагаются вблизи потолка валентной зоны . На зонной схеме (рис. 8.2) донорные уровни обозначаются E_d , акцепторные - E_a, энергия ионизации доноров и акцепторов равны соответственно

.   (8.9)              

              Наличие в полупроводниках небольшого атомов примеси, расположенных на достаточно больших расстояниях друг от друга, приводит к образованию в запрещенной зоне дискретных уровней энергии. При увеличении концентрации примеси волновые функции электронов, вращающихся на боровской орбите, начнут перекрываться. Такое перекрытие должно обусловить “размытие“ примесных энергетических уровней в целую область разрешенных расстояний, которую называют примесной зоной. В германии и кремнии, легированных элементами V группы, примесная зона начинает возникать при концентрациях порядка 10¹⁸  см^-3 атомов примеси.

              Экспериментально установлено, что многие примеси, например Au в кремнии, образуют уровни, лежащие далеко от дна зоны проводимости и, соответственно, от потолка валентной зоны. Эти уровни называют глубокими. Они могут иметь несколько зарядовых состояний. Если мелкие уровни определяют тип проводимости и концентрацию носителей в зонах, то глубокие уровни играют важную роль в процессах рекомбинации  неравновесных электронов и дырок, которые мы рассмотрим далее.

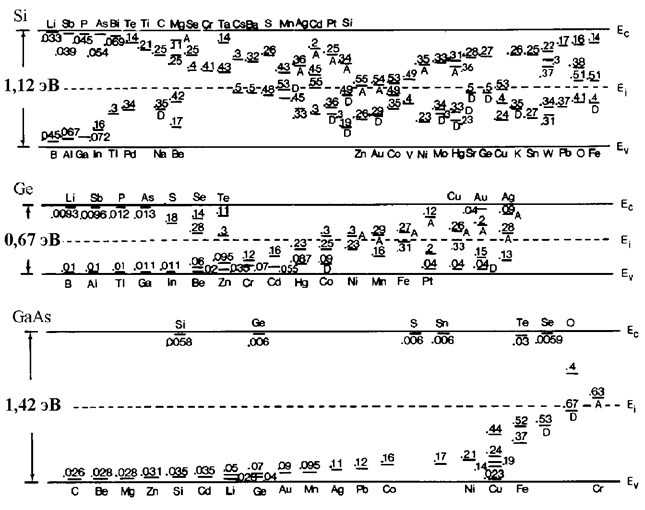
              На рисунке 8.3. приведены энергии ионизации различных примесей в Si, Ge и GaAs.

Рис. 8.3. Энергии ионизации различных примесей в Si, Ge и GaAs.