Структура молекул. Гибридизация (Раздел 2.5. учебного пособия), страница 2

Электронная конфигурация стабильного атома углерода  предполагает наличие двух неспаренных р электронов, т.е. валентность 2, что подтверждается наличием молекулы . Однако, хорошо известны молекулы углерода (), где валентность равна четырем. Можно предположить (как показано в таблице 10), что подобная валентность является просто результатом возбуждения одного электрона, то есть возникновением электронной конфигурации . Энергетических противоречий нет. Затраты энергии на возбуждение электрона с лихвой компенсируются наличием четырех связей, сопровождающихся выделением энергии. Противоречие связано с конфигурацией молекулы. Одна s-орбиталь и три -орбитали не могут создать четыре равноценные, энергетически одинаковой прочности связи, образующие фигуру формы тетраэдра.

Точно с такими же трудностями можно встретиться при рассмотрении валентности бериллия, бора (см. табл. 10) и т.д.

Как было показано [6], состояние любой системы может быть представлено как суперпозиция собственных функций (если они ортогональны и нормированы). В нашем случае можно рассмотреть состояние атома углерода как линейную комбинацию

                               (70)

где i = 1,2,3,4, то есть должно быть получено четыре новых состояния . Критерием выбора  является максимальная, по модулю, энергия связи в молекуле.

Рис. 18.Комбинация двух 1s-волновых функций атома              водорода, образующая симметричную волновую              функцию  молекулярного иона .

Рис. 20. Соотношения между орбиталями отдельных атомов Р,               молекулы  и объединенного атома Не

Рис. 21. Валентные атомные орбитали в . Угол между               связями в действительности равен .

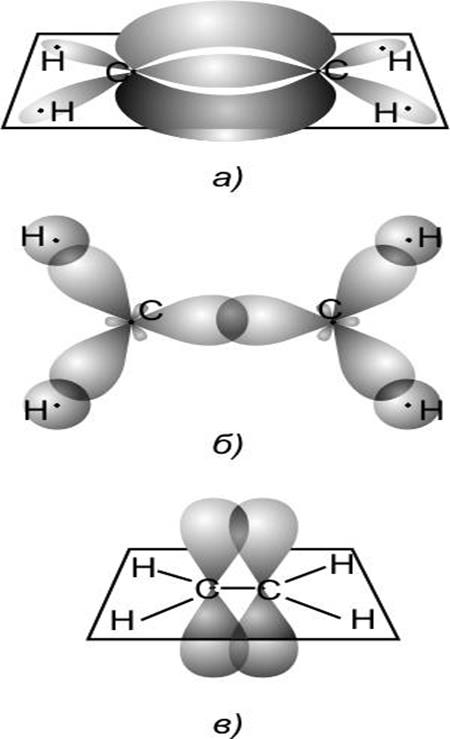
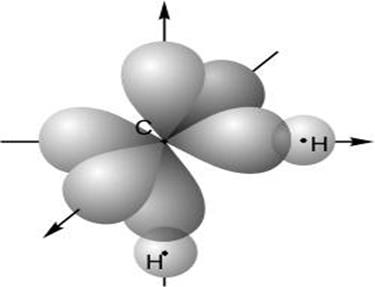
Рис. 22. Молекула этилена (а). Все  атомы лежат в плоскости

              перпендикулярной  плоскости рисунка. Вид  сверху, пока-

               зывающий гибридные -орбитали, образующие -связи

              между  атомами  С,  а  также между  каждым  атомом С и

              двумя  атомами Н(б).  Вид сбоку  показывающий  чистые

              -орбитали, обра зующие -связь между атомами С(в).

Коэффициенты могут быть определены из условия нормировки и ортогональности:  или

,

.

Выберем направление одной из связи  вдоль оси Х. Тогда  и  в этом направлении равны нулю и мы получим

                                          (71)

и ,

окончательно

.                                 (72)

В  входят как радиальные, так и угловые волновые функции. Предположим, в нулевом приближении, что радиальные части собственных функций (69) при заданном n идентичны, то есть не зависят от , тогда сферическую часть (69) можно отнормировать на  и переписать в виде

,

,

,                                         (73)

.

Тогда выражение (72) с учетом (73) в направлении оси связи X ( равно

.                                              (74)

Значение а₁ должно быть таким, чтобы  имело наибольшую величину. Из   находим  а₁ = 1/2 и  из (71) b₁ = /2, следовательно

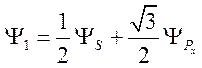.                                             (75)

Предположим, что вторая линия связи расположена в плоскости xz, в которой , тогда

,                                         (76)

,                                                 (77)

.                                                  (78)

Тогда из (75,77,78) находим , следовательно

.

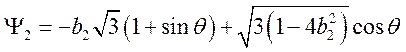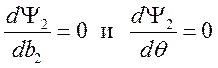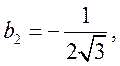
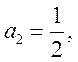
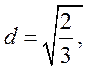
Здесь учтено, что . Из  находим    . Окончательно имеем

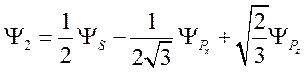                                (79)

и угол между первой и второй гибридной связью , равный тетраэдрическому углу.

Аналогичным образом можно получить

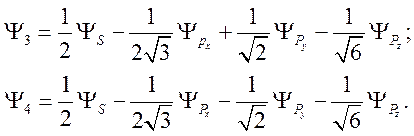                               80)

Все эти функции отличаются друг от друга только поворотом на тетраэдрический угол .

Итак, линейная комбинация (гибридизация)  собственных функций приводит к образованию тетраэдрически ориентированных собственных функций, которые могут обеспечить четыре одинаковых связи. Наиболее ярко подобная связь проявляется в алмазе.

При sp-гибридизации кроме образования тетраэдрических связей, есть большая вероятность образования тригональных связывающих собственных функций, образующих на плоскости между собой углы .