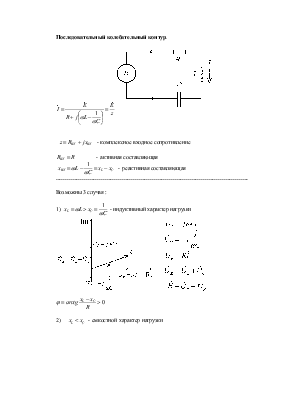





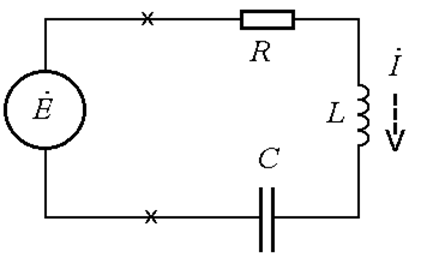
Последовательный колебательный контур.
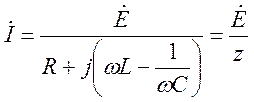
![]() -
комплексное входное сопротивление
-
комплексное входное сопротивление
![]() - активная составляющая
- активная составляющая
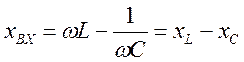 -
реактивная составляющая
-
реактивная составляющая
------------------------------------------------------------------------------------------------------
Возможны 3 случая :
1) 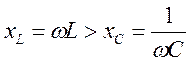 -
индуктивный характер нагрузки
-
индуктивный характер нагрузки
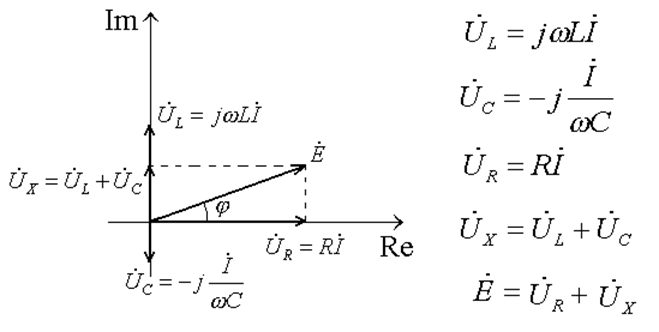
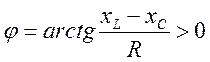
2) ![]() - емкостной характер нагрузки
- емкостной характер нагрузки
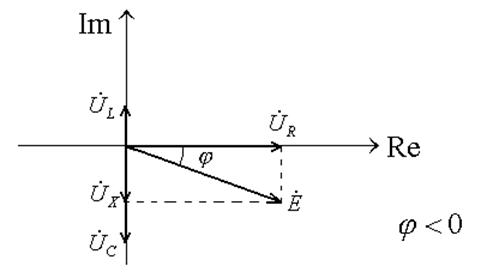
---------------------------------------------------------------------------------------------------
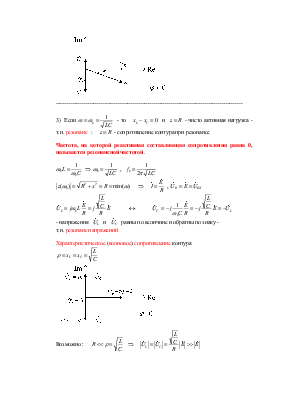
3)
Если 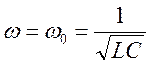 - то
- то ![]() и
и ![]() - чисто активная нагрузка - т.н. резонанс ;
- чисто активная нагрузка - т.н. резонанс ; ![]() - сопротивление контура при резонансе
- сопротивление контура при резонансе
Частота, на которой реактивная составляющая сопротивления равна 0, называется резонансной частотой.
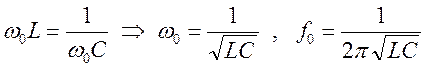
![]() Þ
Þ 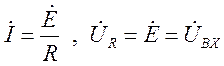
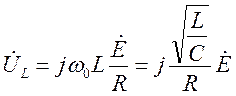 «
« 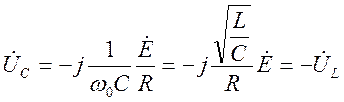
- напряжения ![]() и
и ![]() равны
по величине и обратны по знаку -
равны
по величине и обратны по знаку -
т.н. резонанс напряжений
Характеристическое (волновое) сопротивление контура
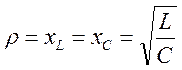
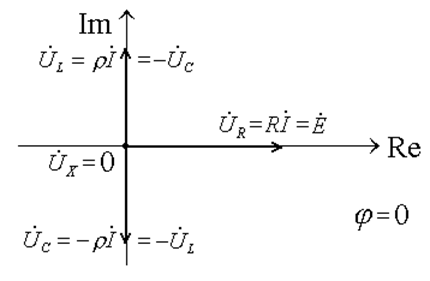
Возможно : 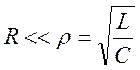 Þ
Þ 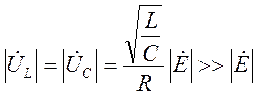
Отношение  - добротность
контура
- добротность
контура
В частности, добротность показывает, во сколько раз при резонансе напряжение на каждом из реактивных элементов выше, чем приложенное к контуру.
------------------------------------------------------------------------------------------------------
Мгновенные значения энергии в L и C при резонансе
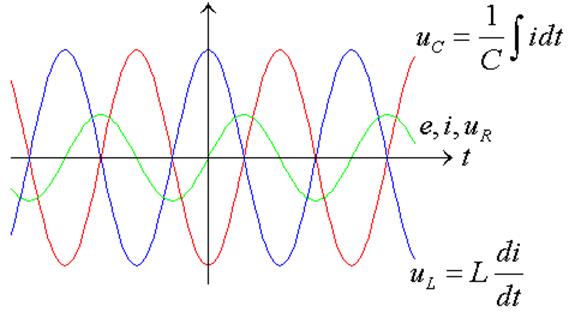
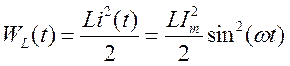
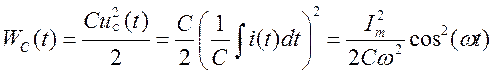
При резонансе 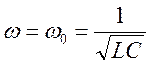 Þ
Þ 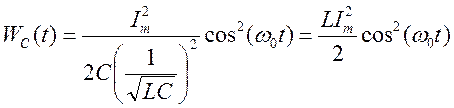
- т.е. при резонансе
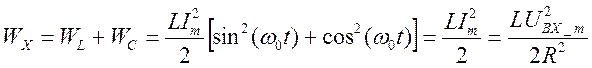 и запасенная в реактивных элементах
энергия "перекачивается" из L в C и наоборот
("колеблется"), сохраняя свою величину
и запасенная в реактивных элементах
энергия "перекачивается" из L в C и наоборот
("колеблется"), сохраняя свою величину
Потери энергии на активном сопротивлении :
мгновенная мощность ![]()
средние потери за период 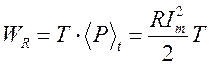 Þ
Þ
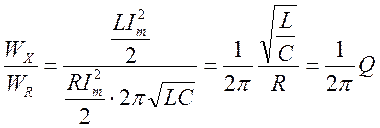 -
т.е. энергия, теряемая за период на активной
составляющей, в
-
т.е. энергия, теряемая за период на активной
составляющей, в ![]() раз меньше энергии, запасенной в
реактивных элементах.
раз меньше энергии, запасенной в
реактивных элементах.
Þ
в другой записи  - добротность через
энергетические соотношения при резонансе
- добротность через
энергетические соотношения при резонансе
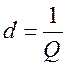 - т.н. затухание
- т.н. затухание
Обычно ![]() - специальными методами
делают контура с
- специальными методами
делают контура с ![]()
------------------------------------------------------------------------------------------------------
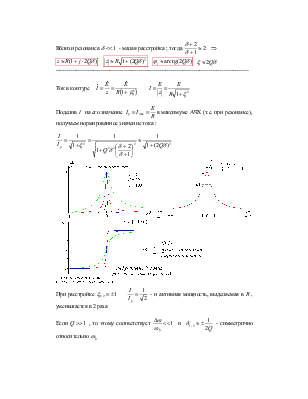
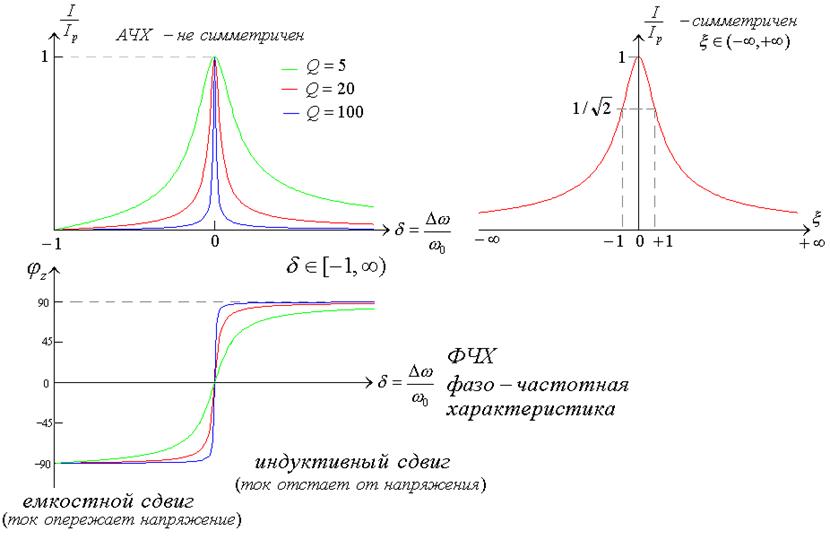
Частотные характеристики - амплитудно-частотная характеристика (АЧХ)
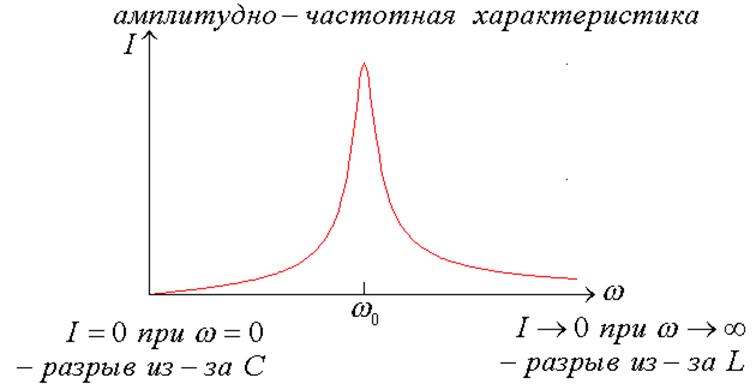
Интересует - поведение АЧХ
вблизи ![]()
Введем 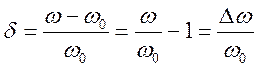 - относительную
расстройку; тогда
- относительную
расстройку; тогда
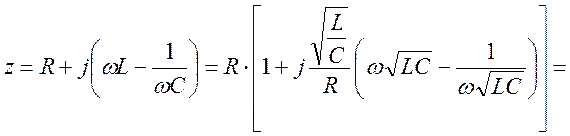
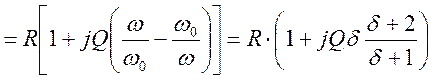
Иногда вводят 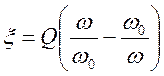 - обобщенную расстройку контура ("кси")
- обобщенную расстройку контура ("кси")
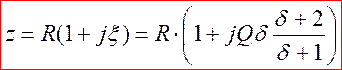


Вблизи резонанса ![]() - малая
расстройка ; тогда
- малая
расстройка ; тогда 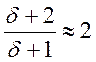 Þ
Þ
![]()
![]()
![]()
![]()
------------------------------------------------------------------------------------------------------
Ток в контуре 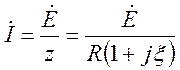
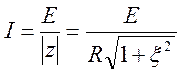
Поделив
![]() на его значение
на его значение 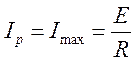 в
максимуме АЧХ (т.е. при резонансе), получаем нормированное значение тока :
в
максимуме АЧХ (т.е. при резонансе), получаем нормированное значение тока :
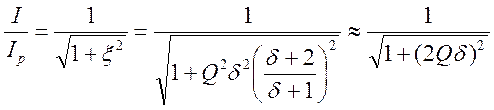
При
расстройке ![]()
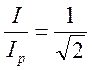 - и
активная мощность, выделяемая в
- и
активная мощность, выделяемая в ![]() , уменьшается в 2 раза
, уменьшается в 2 раза
Если
![]() , то этому соответствует
, то этому соответствует 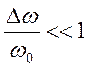 и
и 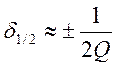 -
симметрично относительно
-
симметрично относительно ![]()
При
малых добротностях максимум смещен, но выполняется соотношение 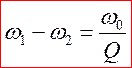 - полоса частот
вблизи резонансной, на границах которой ток снижается до
- полоса частот
вблизи резонансной, на границах которой ток снижается до ![]() от резонансного, а рассеиваемая мощность
снижается в два раза, называется полосой пропускания контура.
от резонансного, а рассеиваемая мощность
снижается в два раза, называется полосой пропускания контура.
Соответственно, добротность колебательного контура - так же отношение его резонансной частоты к полосе пропускания.
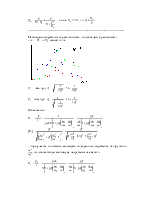
На границах полосы пропускания активная и реактивная составляющие сопротивления равны по величине :
![]() ,
, ![]() Þ
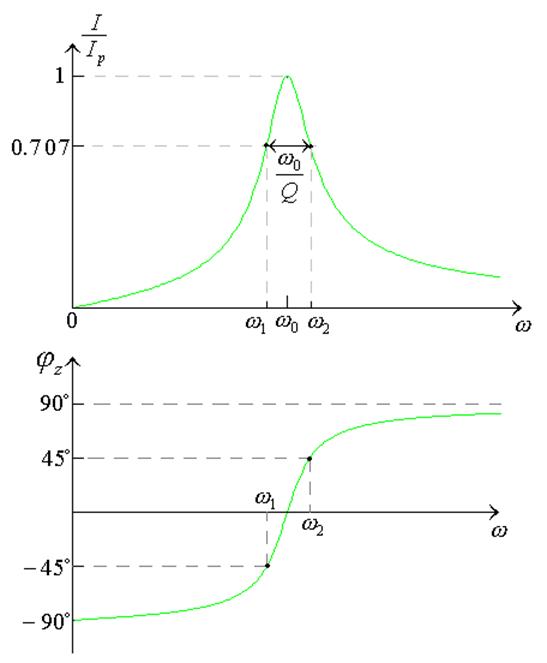
Þ ![]() - т.е. на границах полосы пропускания
сдвиг фазы тока равен ±45° :
- т.е. на границах полосы пропускания
сдвиг фазы тока равен ±45° :
------------------------------------------------------------------------------------------------------
Влияние параметров генератора на избирательность
Ранее
негласно полагали, что ![]() - т.е. выходное напряжение
источника не зависит от тока. Если же
- т.е. выходное напряжение
источника не зависит от тока. Если же ![]() , то
избирательность ухудшается :
, то
избирательность ухудшается :
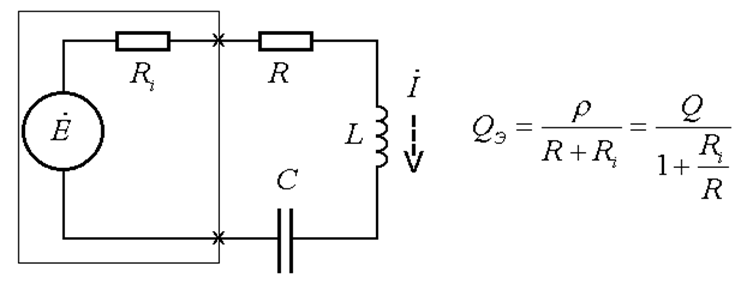
Þ для достижения
избирательности выгодно применять последовательный колебательный контур, если
внутреннее сопротивление источника достаточно мало (![]() )
)
------------------------------------------------------------------------------------------------------
Добротность нагруженного колебательного контура
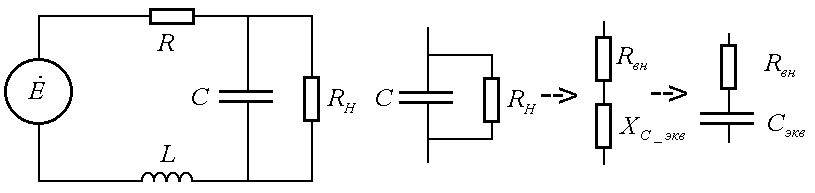
![]()
![]()
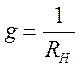
![]()
![]()
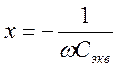
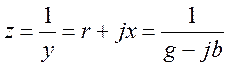 Þ
Þ 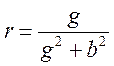 ,
, 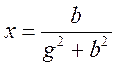 Þ
Þ
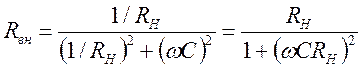
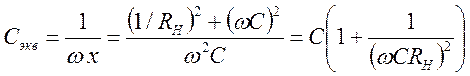
Если контур нагружен не
сильно и ![]() , то
, то 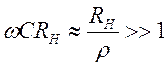 ;
тогда
;
тогда
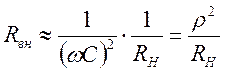 и
и ![]()
Т.о. добротность нагруженного контура
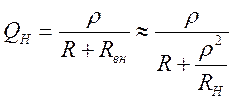 и если
и если ![]() , то
, то 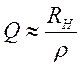 .
.
------------------------------------------------------------------------------------------------------
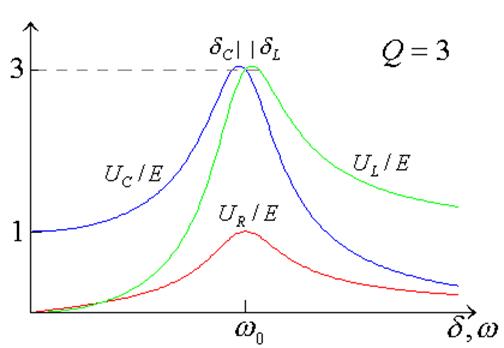
Максимумы напряжения на реактивностях - не совпадают с резонансом !
- т.к. ![]()
![]() и
и ![]() зависят от
зависят от ![]()
![]() при
при 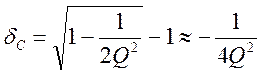
![]() при
при 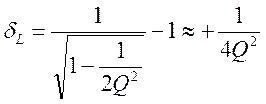
Обоснование :
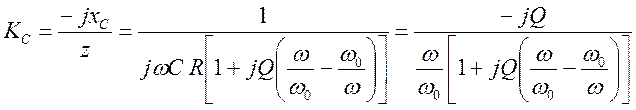
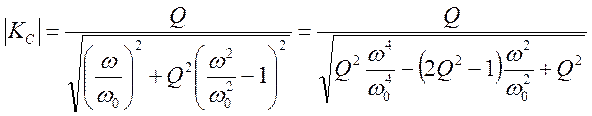
-
определяется положение минимума подкоренного выражения как функции ![]() , что соответствует максимуму напряжения на
емкости
, что соответствует максимуму напряжения на
емкости
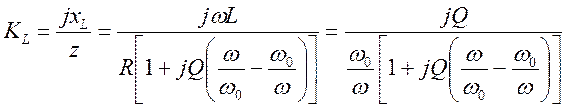
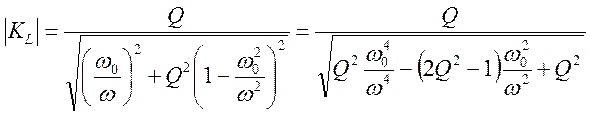
-
определяется положение минимума подкоренного выражения как функции ![]() , что соответствует максимуму напряжения на
индуктивности
, что соответствует максимуму напряжения на
индуктивности
------------------------------------------------------------------------------------------------------
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.