Основы теории переноса излучения. Введение и основные понятия, страница 2

Представим себе неограниченную излучающе-поглощающую среду, находящуюся в состоянии термодинамического равновесия при постоянной температуре Т. В стационарном случае поле излучения также будет равновесно. Это означает, что число квантов или количество лучистой энергии, испускаемых веществом 1сек в 1см³ в данном интервале частот dv и в данном интервале направлений должно быть равно числу поглощаемых квантов или количеству поглощаемой веществом лучистой энергии в тех же интервалах dv, . Поле равновесного излучения изотропно, т.е. не зависит от направления и от конкретных свойств среды, являясь универсальной функцией частоты и температуры. Спектральная плотность равновесного излучения U_vpбыла получена Планком на основе квантовой статистики для фотонного газа.

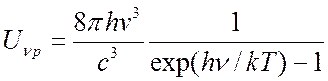                                                      (12.10).

Поскольку 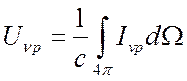 и I_vpне зависит от  то:

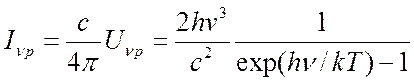                                        (12.11).

В астрофизике часто вместо I_vp употребляется обозначение B_v.

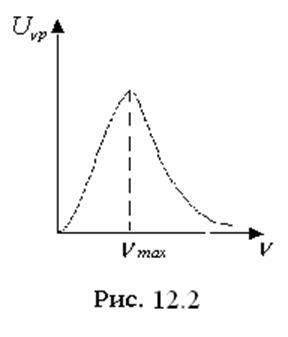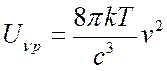Построим график U_vp (рис. 12.2). При малых vU_vpведет себя как парабола, при больших vкак экспонента; . Основная доля лучистой энергии переносится квантами в диапазоне частот от инфракрасной области, до ультрафиолетовой, доля энергии в остальных участках спектра менее 1% от всей энергии. При повышении температуры максимум смещается в сторону больших частот. В области малых частот   - закон Рэлея-Джинса. В области больших частот 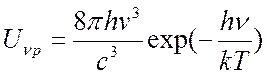 - формула Вина.

 Полная плотность равновесного излучения есть

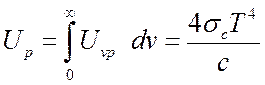                                                                (12.12),

где 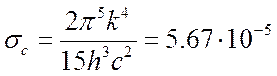 - постоянная Стефана-Больцмана.

Очевидно для равновесного излучения, полный спектральный поток равен нулю, т.е. через любую поверхность справа налево и слева направо потоки в точности равны и противоположны по направлению, а односторонний поток

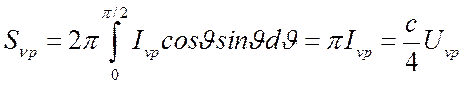                                  (12.13).

Интегральный по спектру односторонний поток получим из (12.13) интегрированием по всему спектру

                                                                      (12.14).

Рассмотрим теперь неограниченную среду, находящуюся при температуре Т в термодинамическом равновесии, внутри которой имеется полость, заполненная излучением. Очевидно, что излучение также будет равновесным. Из полости на поверхность вещества падает поток S_vр, этот поток частично отражается от поверхности, а частично проходит во внутрь среды и поглощается. Пусть коэффициент отражения R_v, а поглощающая способность вещества А_vи А_v = 1 – R_v. Количество излучения, которое поглотится в веществе есть , в силу равновесия такое же количество излучения должно излучиться в сторону полости, которое есть по определению лучеиспускательная способность поверхности , т. е.  и отношение

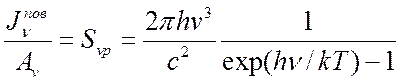                                             (12.15)

есть универсальная функция температуры, известное как закон Кирхгофа, в то время как поглощающая способность, коэффициент отражения, лучеиспускательная способность поверхности являются характеристиками состояния вещества.

Тело, которое полностью поглощает все падающее на него излучение, называется абсолютно черным. Для него по определению R_v= 0, А_v= 1, с поверхности его выходит поток S_vр, а интегральный по спектру поток есть .

Уравнения радиационной газодинамики.

          В задачах теплофизики и газодинамики знание характеристик поля излучения необходимо в основном для расчета газодинамических полей и теплообмена, т.е. для решения уравнений гидродинамики в присутствии поля излучения. В общем случае перенос излучения и лучистый теплообмен влияют на состояние вещества и на его движение.

          Для оценки вклада радиационных членов в уравнении РГД заменим поток излучения 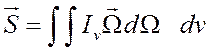 односторонним равновесным потоком . При этом будем считать, что для газодинамических величин справедливо , тогда для уравнений РГД (1.1) -- (1.3), (1.32) -- (1.38) можно записать следующие оценочные соотношения

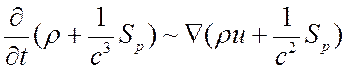                                                              (12.16),

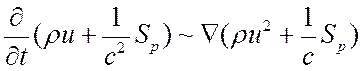                                                            (12.17),

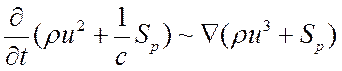                                                     (12.18).

Из (12.16) – (12.18) следует, что наибольший вклад радиационного поля в исходной системе уравнений связан с потоком энергии излучения в правой части уравнения энергии. Если считать, что ru³~S_р, то плотность энергии излучения в левой части уравнения энергии и давление излучения в правой части уравнения движения отличаются от соответствующих газодинамических множителем ~ и/с, а радиационные члены, учитывающие импульс фотонов и поток массы, связанной с переносом излучения – множителем ~ (и/с)².

Проведем оценку для типичных параметров высокоскоростного потока: р ~ 10 бар, и ~ 1 км/с. Тогда из условия  следует оценка на температуру, при которой необходим учет потока энергии излучения , что соответствует уровню температур за отраженной от тела ударной волной. Учет плотности энергии излучения и давления необходим при температурах , а в связи с тем, что при таких температурах давление газа и его внутренняя энергия значительно возрастают за счет многократной ионизации, необходимая температура становится еще выше. В земных условиях подобная ситуация может возникнуть только при исследовании задач, связанных с ядерными взрывами и управляемым термоядерным синтезом, а так же высокоскоростным соударением тел. Вкладом радиационных членов, пропорциональных (и/с)² практически всегда пренебрегают. Таким образом, в практических задачах радиационной газодинамики наличие радиационного поля сводится к учету дивергенции лучистого потока в правой части уравнения энергии.