Некоторые приложения двойных и тройных интегралов, страница 2

Следствия.

а) Если плоская кривая l задана явно: , и , то

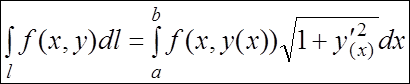                                 .                                      (5.2)

б) Если плоская кривая l задана в полярных координатах: , то

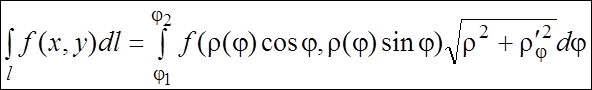                               .             (5.3)

Некоторые приложения КИ-1

1. Масса материальной линии. Пусть , - линейная плотность массы материальной линии l. Тогда масса этой линии есть:

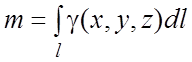                                            .                                                         (5.4)

2. Длина пространственной (или плоской) кривой l есть L:   .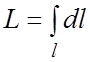

3. Статические моменты и координаты центра тяжести.

 а) Для плоской линии  c плотностью  и массой m статические моменты относительно координатных осей Oy и Ox: 

                                             ,       ;

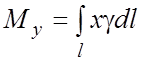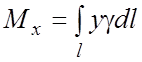координаты центра тяжести:

                                            ,         .

б) Для пространственной линии l c плотностью  и массой m статические моменты относительно плоскостей  и Oxy:

                       ,       ,           ;

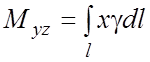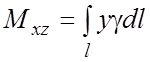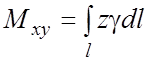  координаты центра тяжести:

                      ,      ,     .

Пример 17. Вычислить КИ-1: 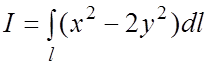, где l – прямолинейный отрезок, соединяющий точки  и .

Ñ Уравнения отрезка прямой AB в параметрической форме: 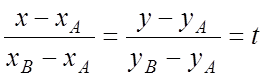,  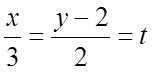  или . Тогда 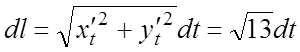 и из (5.1) имеем  .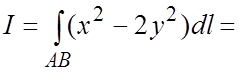

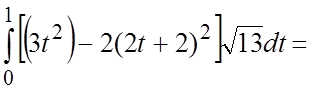
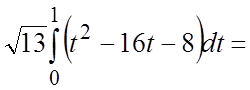
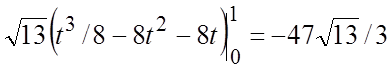Замечание. В случае явного задания отрезка прямой    следует воспользоваться формулой (5.2). #

Пример 18. Вычислить КИ-1: 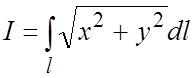, где l– кривая, заданная уравнением  при условии .

Ñ Для построения кривой l преобразуем уравнение ее к виду ; таким образом, l есть полуокружность с центром в точке  радиуса 1, расположенная слева от  оси Oy (рис. 14.22).

Наличие комбинации  в подынтегральной функции и в уравнении l наводит на мысль провести вычисления в полярных координатах, которые связаны с декартовыми координатами формулами . Тогда: из
               Рис. 14.22          получаем  – уравнение l в полярных координатах; из рис. 14.22 (или условий , ,  следует: 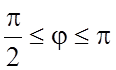; 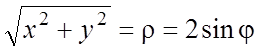, 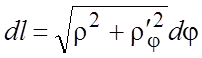= ==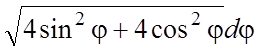,  и  из (5.3)   . #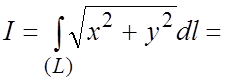

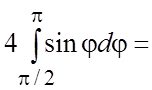
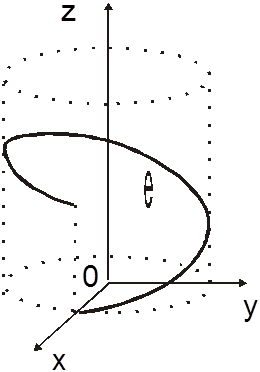
Пример 19. Найти массу одного витка материальной винтовой линии , ,  (рис. 14.23), если линейная плотность в точке обратно пропорциональна квадрату расстояния этой точки от начала координат.

Ñ По условию задачи плотность +

 =, где k – коэффициент про-

L

Рис.14.23.

порциональности, . Для одного витка  . Из формул (5.4) и (5.1) имеем:  =  

=   . #

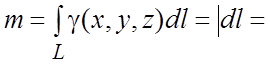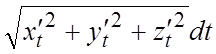
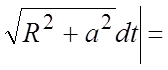
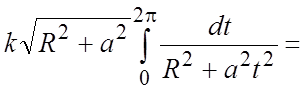
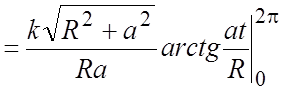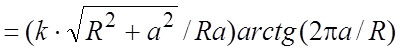Задачи для самостоятельного решения

Вычислить криволинейные интегралы первого рода:

81. 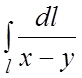, где l – отрезок прямой , заключенный между точками  и .

82. 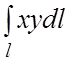, где l – контур прямоугольника с вершинами:   .

83. 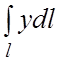, где l– дуга параболы , отсеченная параболой .

84. 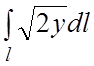, где l– первая арка циклоиды .

85. 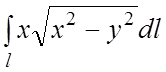, где l- половина лемнискаты   .

86. 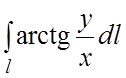, где l – часть спирали Архимеда , заключенная внутри круга радиуса R с центром в точке .

87. 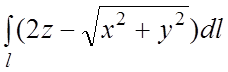, где l – первый виток конической винтовой линии ,  , .

88. 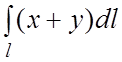, где l –четверть окружности , лежащая в первом октанте.

89. 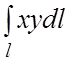, где l – дуга гиперболы ,  .

90. 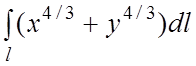, где l– дуга астроиды  в первом квадранте.

91. Найти массу первого витка винтовой линии , плотность которой в каждой точке равна полярному радиусу этой точки. 

92. Найти массу линии , , от точки, соответствующей t=0, до произвольной точки, если плотность в каждой точке обратно пропорциональна квадрату полярного радиуса и в точке равна единице.

93. Найти массу дуги параболы , если линейная плотность в текущей точке равна .

Вычислить координаты центра тяжести дуги однородной кривой :

94. , от точки до точки .

95. .

96. .

14.5.2       Криволинейные интегралы второго рода (КИ-2)

          Пусть : 1) в точках непрерывной кривой AB из пространства  определены ограниченные скалярные функции ;

2) - произвольное разбиение кривой AB на элементарные дуги с длинами  и проекциями , ,  на соответствующие оси координат;  3) - произвольный набор точек;

4) 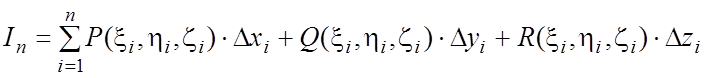- интегральная сумма, соответствующая данному разбиению и данному выбору точек.

       Определение. Конечный предел интегральной суммы  при  , не зависящий ни от способа разбиения AB , ни от выбора точек , называется криволинейным интегралом второго рода от функций по пути AB:   .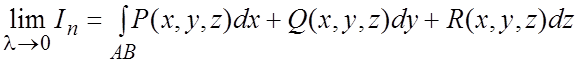

Механически КИ-2 представляет собой работу переменной силы , точка приложения которой описывает кривую AB.