











4. Координаты центра тяжести материальной поверхности s :
![]() .
.
Задания
1. Записать линейные свойства ПИ-1.
2. Записать свойство аддитивности для ПИ-1.
Пример 23.
Вычислить ПИ-1 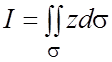 , где s - часть плоскости
, где s - часть плоскости
![]() , вырезанная цилиндром
, вырезанная цилиндром ![]() (рис.14.26).
(рис.14.26).
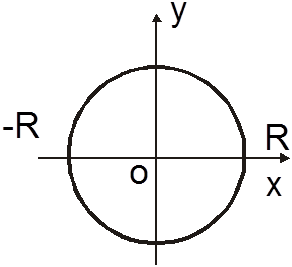 |
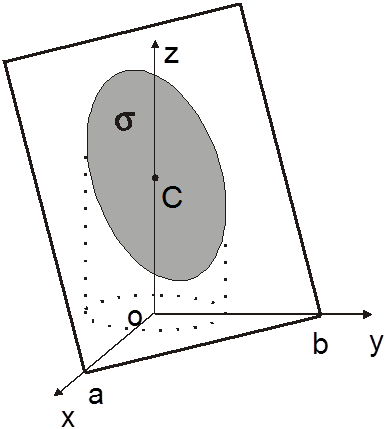
Рис. 14.26
Ñ Поверхность s проецируется на плоскость ![]() в круг
в круг ![]() . По
формуле (6.4)
. По
формуле (6.4) 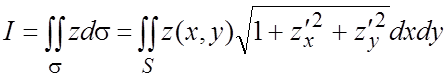 . Из уравнения s следует
. Из уравнения s следует ![]() ,
, ![]()
![]()
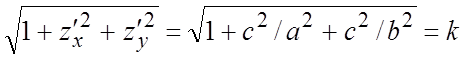 ; тогда
; тогда
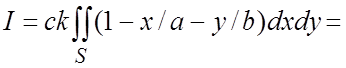
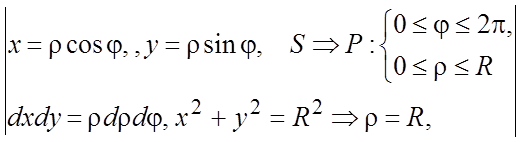 =
=
=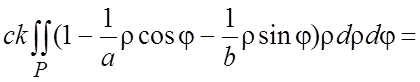
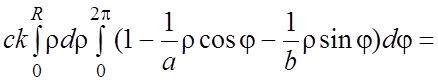
=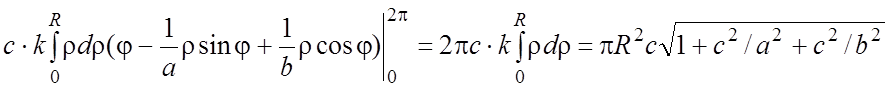 .#
.#
Пример 24. Вычислить ПИ-1 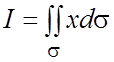 , где s - полная поверхность тетраэдра, отсекаемого от первого
октанта плоскостью
, где s - полная поверхность тетраэдра, отсекаемого от первого
октанта плоскостью ![]() .
.
Ñ Полная поверхность s тетраэдра складывается из его
граней: ![]() ,где
,где![]() (рис.14.27).
(рис.14.27).
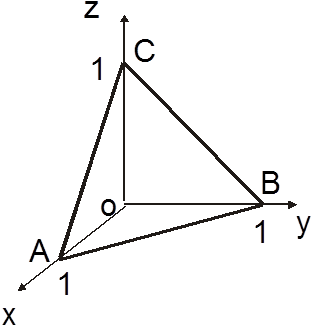 Выпишем уравнения поверхностей
Выпишем уравнения поверхностей ![]() и вычислим для них элементы
и вычислим для них элементы ![]() :
:
а) 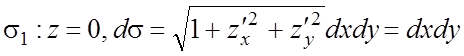 ;
;
б) 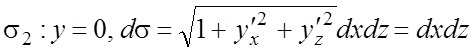 ;
;
|
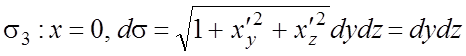 ;
;
г) 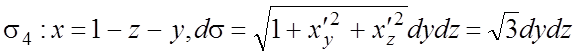 .
.
Задав уравнения поверхностей в явном
виде, мы определили тем самым плоскости проецирования их; ![]() - области, на которые проецируются
- области, на которые проецируются ![]() .
.
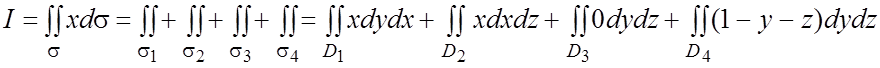 .
.
По поводу последней записи напомним,
что следует в подынтегральной функции ![]() независимые
переменные (переменные из области
независимые
переменные (переменные из области ![]() ) оставлять без изменения,
зависимую переменную заменить из явного уравнения соответствующей поверхности,
а
) оставлять без изменения,
зависимую переменную заменить из явного уравнения соответствующей поверхности,
а ![]() заменить выражением, полученным выше,
причем
заменить выражением, полученным выше,
причем ![]() . Находим:
. Находим:
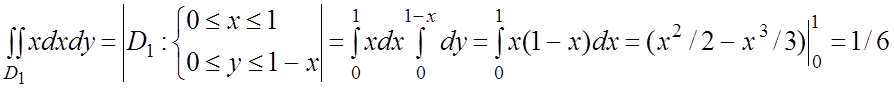 ;
;
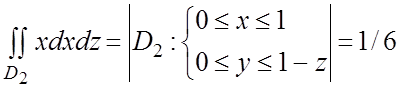 , так как области
, так как области ![]() и
и ![]() переходят
одна в другую заменой
переходят
одна в другую заменой ![]() на
на ![]() ;
;
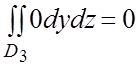 ;
;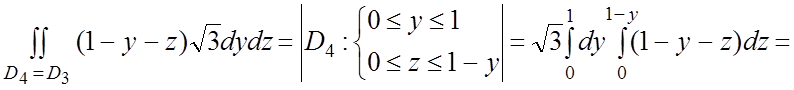
=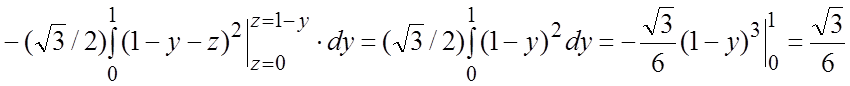 .
.
![]() .#
.#
Вычислить поверхностные интегралы первого рода:
120. 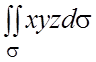 , где s - часть плоскости
, где s - часть плоскости ![]() , лежащая в первом октанте.
, лежащая в первом октанте.
121. 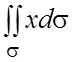 , где s - часть сферы
, где s - часть сферы ![]() , лежащая в первом октанте.
, лежащая в первом октанте.
122. 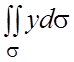 , где s - полусфера
, где s - полусфера 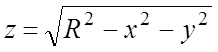 .
.
123. 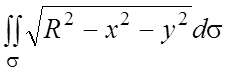 , где s - полусфера
, где s - полусфера 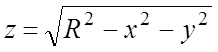 .
.
124. 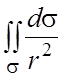 , где s - цилиндр
, где s - цилиндр ![]() ,
ограниченный плоскостями
,
ограниченный плоскостями ![]() , а r –расстояние от точки поверхности до
начала координат.
, а r –расстояние от точки поверхности до
начала координат.
125. 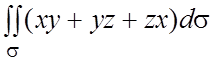 , где s - часть конической поверхности
, где s - часть конической поверхности 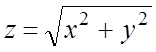 , вырезанная поверхностью
, вырезанная поверхностью ![]() .
.
126. Найти массу сферы, если поверхностная плотность в каждой точке равна расстоянию этой точки от некоторого фиксированного диаметра сферы.
127. Найти массу параболической оболочки ![]() , плотность которой меняется по закону
, плотность которой меняется по закону ![]() .
.
128. Найти массу полусферы ![]() , плотность которой в каждой ее точке равна
, плотность которой в каждой ее точке равна
![]() .
.
129. Найти координаты центра тяжести
части однородной поверхности 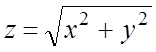 , вырезанной
поверхностью
, вырезанной
поверхностью ![]() .
.
14.6.3. Поверхностные интегралы второго рода (ПИ-2)
Пусть : 1) в точках
двусторонней гладкой (или кусочно- гладкой) поверхности s задана ограниченная функция ![]() ; 2) выбрана положительная сторона
поверхности; 3)
; 2) выбрана положительная сторона
поверхности; 3) ![]() - разбиение s на nчастей
- разбиение s на nчастей ![]() с площадями
с площадями ![]() и диаметрами
и диаметрами ![]() ; 4)
; 4) ![]() - произвольный набор точек;
- произвольный набор точек;
5) ![]() - проекция элемента
- проекция элемента ![]() на
плоскость
на
плоскость ![]() (проекция определенной стороны поверхности
связана со знаком “+” или “–“ ); 6)
(проекция определенной стороны поверхности
связана со знаком “+” или “–“ ); 6) 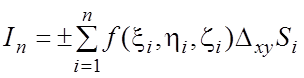 - интегральная сумма,
соответствующая данному разбиению и выбору точек.
- интегральная сумма,
соответствующая данному разбиению и выбору точек.
Определение. Конечный предел ![]() при
при ![]() называется
поверхностным интегралом второго рода от
называется
поверхностным интегралом второго рода от ![]() по
определенной стороне поверхности s :
по
определенной стороне поверхности s :
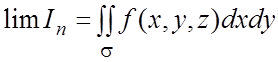
(здесь ![]() напоминает
о проекции
напоминает
о проекции ![]() на
на ![]() и
содержит знак).
и
содержит знак).
При проецировании
ориентированной поверхности s на плоскости ![]() и
и ![]() получаем
ПИ-2:
получаем
ПИ-2:
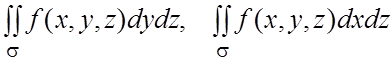 .
.
Вычисление ПИ-2.
Теорема 14.11. Пусть
ориентированная гладкая поверхность ![]() задана явно. Тогда
задана явно. Тогда
а) если ![]() , то
, то 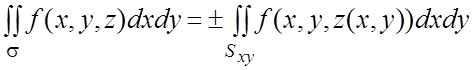 ;
;
б) если ![]() , то
, то 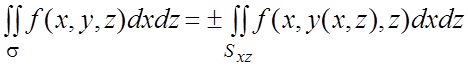 ; (6.5)
; (6.5)
в) если ![]() , то
, то 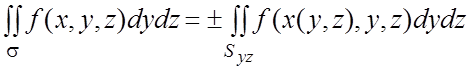 .
.
Связь между ПИ-1 и ПИ-2. Теорема
14.12. Если s - гладкая двусторонняя поверхность,
ориентация s
характеризуется нормалью ![]() =
=![]()
![]() - функции, определенные и непрерывные на s, то
- функции, определенные и непрерывные на s, то
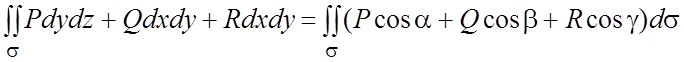 . (6.6)
. (6.6)
Связь между ПИ-2 и
тройным интегралом (формула Гаусса – Остроградского). Теорема 14.13. Пусть
функции ![]() - непрерывные вместе со своими частными
производными (первого порядка) в некоторой пространственной области V, ограниченной гладкой замкнутой поверхностью
s с положительной внешней стороной.
Справедлива формула
- непрерывные вместе со своими частными
производными (первого порядка) в некоторой пространственной области V, ограниченной гладкой замкнутой поверхностью
s с положительной внешней стороной.
Справедлива формула
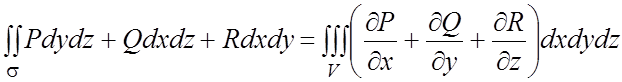 .
.
Замечание. О приложениях ПИ-2 смотри в разделе “Элементы теории поля”.
Пример 25. Вычислить ПИ-2: 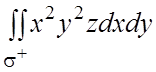 , где
, где ![]() - положительная
(внешняя) сторона сферы.
- положительная
(внешняя) сторона сферы.
|
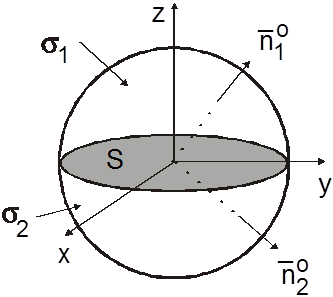 Ñ Для вычисления ПИ-2 замкнутую
поверхность
Ñ Для вычисления ПИ-2 замкнутую
поверхность 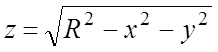 и
и 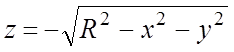 (рис.14.28).
Тогда на основании (6.2) положительная сторона поверхности
(рис.14.28).
Тогда на основании (6.2) положительная сторона поверхности ибо угол между ![]() и положительным направлением Oz, т.е. (
и положительным направлением Oz, т.е. (![]() ,ÙOz), – острый, а положительная сторона
поверхностности
,ÙOz), – острый, а положительная сторона
поверхностности ![]() - вектором
- вектором ![]() , ибо угол (
, ибо угол (![]() ,ÙOz)- тупой. Проекция каждой из поверхностей
,ÙOz)- тупой. Проекция каждой из поверхностей
![]() и
и ![]() есть
область
есть
область ![]() - круг радиуса R с центром в начале координат. Поэтому по формуле
(6.5)
- круг радиуса R с центром в начале координат. Поэтому по формуле
(6.5) 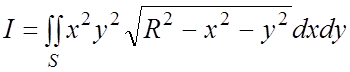 +
+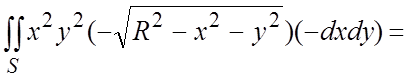 =
=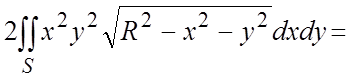 ½переходим к полярным координатам :
½переходим к полярным координатам : ![]()
![]() ,
, ![]() ½= =
½= =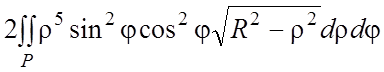 =
= 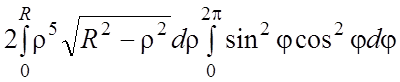 =½двойной интеграл “расщепился” в произведение определенных
интегралов½=
=½двойной интеграл “расщепился” в произведение определенных
интегралов½=![]() ;
;
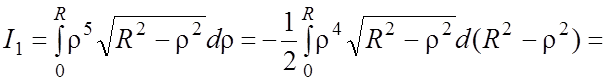
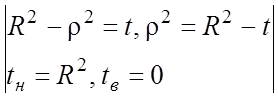 =
=
=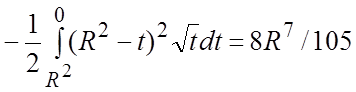 ;
; 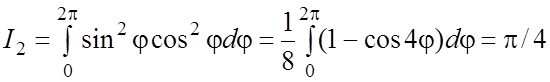 .
.
Итак, ![]() . #
. #
Пример 26. Вычислить ПИ-2 общего вида: 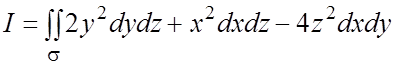 , где
, где ![]() -
внешняя сторона конической поверхности
-
внешняя сторона конической поверхности 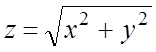 ,
ограниченной плоскостью z=2.
,
ограниченной плоскостью z=2.
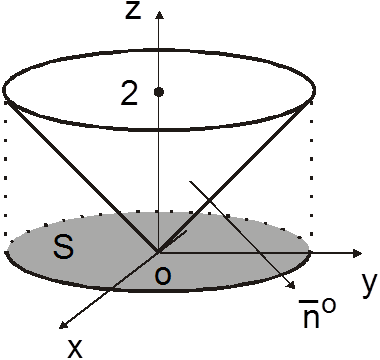 ÑВнешняя сторона поверхности
ÑВнешняя сторона поверхности ![]() характеризуется нормальным вектором,
который составляет тупой угол с положительным направлением оси Oz (рис.14.29),
характеризуется нормальным вектором,
который составляет тупой угол с положительным направлением оси Oz (рис.14.29),
|
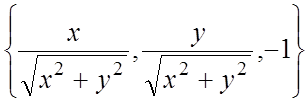 ,
, 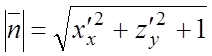 =
= 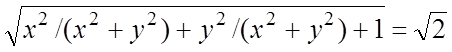 .
.
Тогда 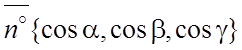 ,
,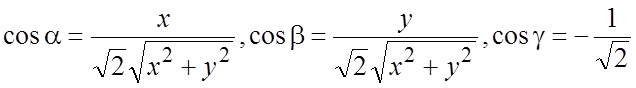 .
.
Данный ПИ-2 можно вычислять по разному. Первый способ – вычислять три ПИ-2, составляющих данный поверхностный интеграл. Второй способ – использовать связь ПИ-2 с ПИ-1, что и сделаем. По формуле (6.6)
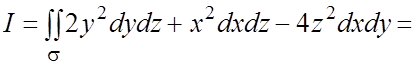
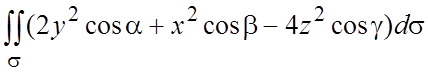 =
=
|
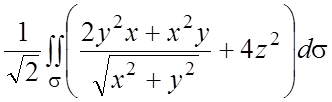 .
Последний поверхностный интеграл есть ПИ-1. Проекция
.
Последний поверхностный интеграл есть ПИ-1. Проекция 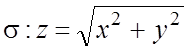 на плоскость Oxy есть область
на плоскость Oxy есть область 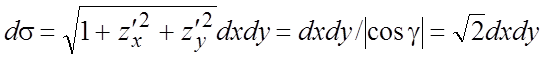 , то по
формуле (6.3) (или (6.4))
, то по
формуле (6.3) (или (6.4)) 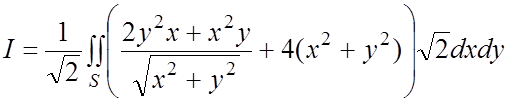 =½переходим к полярным координатам
=½переходим к полярным координатам 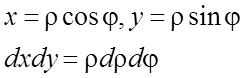
=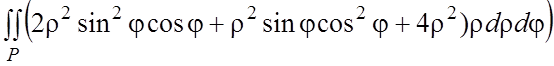 = =
= =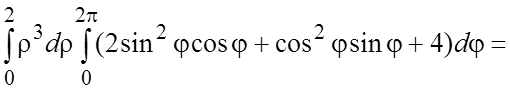
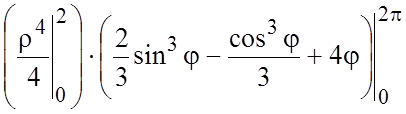 =
= ![]() .#
.#
Задачи для самостоятельного решения
Вычислить следующие поверхностные интегралы второго рода:
130. 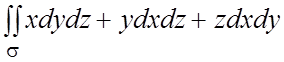 , где s - положительная сторона куба,
составленного плоскостями
, где s - положительная сторона куба,
составленного плоскостями ![]() .
.
131. 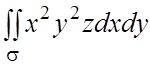 , где s - положительная сторона нижней
половины сферы
, где s - положительная сторона нижней
половины сферы ![]() .
.
132. 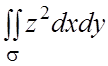 , где s - внешняя сторона эллипсоида
, где s - внешняя сторона эллипсоида 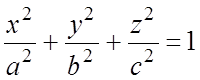 .
.
133. 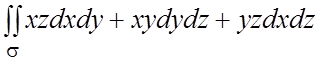 , где s - внешняя сторона пирамиды,
составленной плоскостями
, где s - внешняя сторона пирамиды,
составленной плоскостями ![]() .
.
Применяя формулу Гаусса –
Остроградского, преобразовать следующие поверхностные интегралы, если гладкая
поверхность s ограничивает
конечную область (тело) V
и ![]() ,
, ![]() ,
, ![]() - направляющие косинусы внешней нормали к s:
- направляющие косинусы внешней нормали к s:
134. 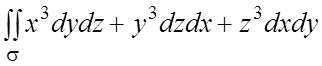 .
135.
.
135. 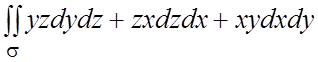 .
.
136. 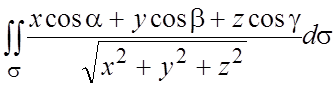 .
.
137. 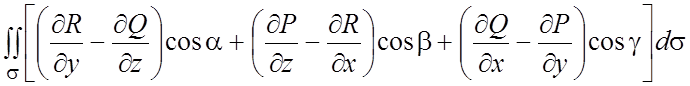 .
.
138. 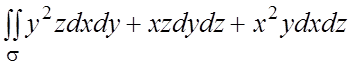 , где s - внешняя сторона поверхности, расположенной
в первом октанте и составленной из параболоида
, где s - внешняя сторона поверхности, расположенной
в первом октанте и составленной из параболоида ![]() ,
цилиндра
,
цилиндра ![]() и координатных плоскостей.
и координатных плоскостей.
139. Вычислить интегралы 132, 133, применяя формулу Гаусса – Остроградского.
Ответы
1. 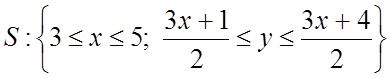 . 2.
. 2. ![]() .
.
3. ![]() . 4. 1. 5. 1/ 40. 6.
. 4. 1. 5. 1/ 40. 6. ![]() .
.
7. ![]() . 8.
. 8. 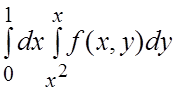 . 9.
. 9.
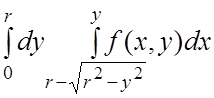 . 10.
. 10.
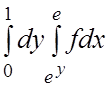 . 11.
. 11. 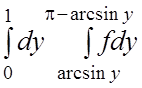 . 12.
. 12.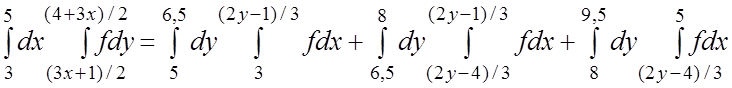 .
.
13. 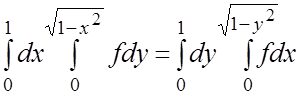 . 14.
. 14. 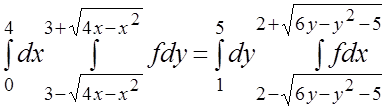 .
.
15. 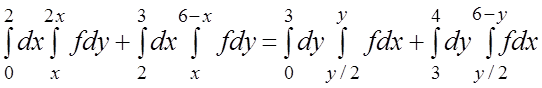 .
.
16. 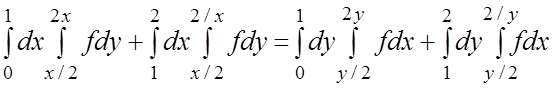 .
.
17. 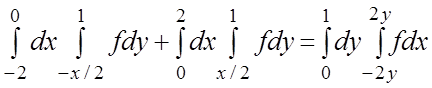 . 18.
. 18. 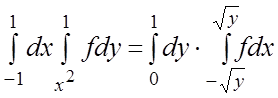 .
.
19. ![]() . 20. 0. 21.
33/140. 22. 9/4. 23. –2. 24.
. 20. 0. 21.
33/140. 22. 9/4. 23. –2. 24. ![]() .
.
25. ![]() . 26.
. 26. ![]() .
27.
.
27. 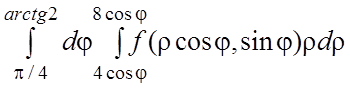 .
.
28. 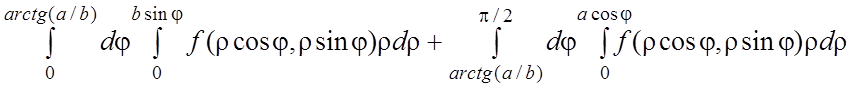 .
.
29. 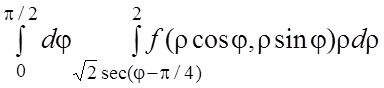 . 30.
. 30. 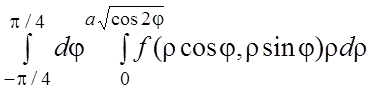 .
.
31. 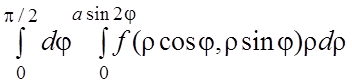 .
.
32. 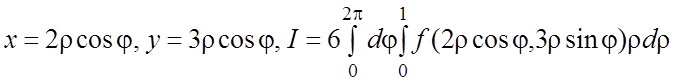 .
.
33. 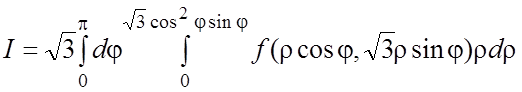 .
.
34. 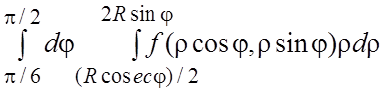 . 35.
. 35. 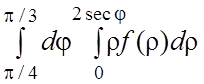 .
.
36. 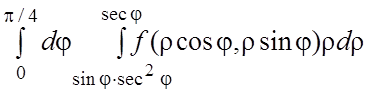 . 37.
. 37.![]() .
.
38. ![]() . 39.
. 39. ![]() .
40.
.
40. ![]() . 41.
. 41. ![]() .
42.
.
42. ![]() . 43.
. 43. ![]() .
.
44. а) ![]() ,
, ![]() ;
;
б) ![]() .
.
45. а) 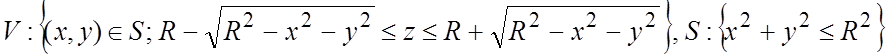 ;
;
б) 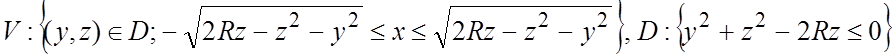 .
.
46. а) ![]() ;
;
б) 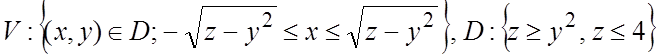 .
.
47. ![]() . 48.
. 48. ![]() .
49. 1/180. 50.
.
49. 1/180. 50. ![]() . 51.
. 51. ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.