Определение закона изменения угловой скорости платформы

Задание для контрольной работы по теоретической механике (динамика Д3)
	a. Однородная горизонтальная платформа (прямоугольная плита со сторонами 2R и R, R=0.5м) имеющая массу m1=16 кг, жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси z с угловой скоростью w0=2 с-1. В момент времени t0=0 на вал начинает действовать вращающий момент М=6t, направленный противоположно w0; одновременно груз D массой m2=10 кг, находящийся в желобе AB в точке С, начинает двигаться по желобу под действием внутренних сил по закону s=CD=0.4t2. Определить закон изменения угловой скорости платформы w=f(t).
	b. Механическая система состоит из грузов 1 и 2 (m1=0кг, m2=6кг), ступенчатого шкива 3 (m3=4кг) с радиусами ступеней R3=03.м и r3=0.1м и радиусом инерции относительно оси вращения r3=0.2м, блока 4 (m4=0) радиуса R4, подвижного блока 5 (m5=5кг). Тело 5 считать сплошным однородным цилиндром. Коэффициент трения грузов о плоскость f=0.1.  Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. К одному из тел прикреплена пружина с коэффициентом жесткости c=200 Н/м, ее начальная деформация равна нулю.  Система приводится в движение из состояния покоя под действием силы F=80(4+5s) Н, зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М=1.2 Н*м сил сопротивления. Определить w3 в тот момент времени, когда s=0.2 м.

Решение задачи  a

Рассмотрим механическую систему, состоящую из платформы и груза D. Для определения w применим теорему об изменении кинетического момента системы относительтно оси z :

На систему действуют внешние силы Р1, Р2 (вес платформы и груза), реакции в оси и момент М. Все силы параллельны или пересекают ось z, поэтому в сумму моментов в правой части теоремы они не войдут, так как их моменты относительно оси z равны нулю. Тогда, считая положительным направление w0 против хода часовой стрелки, запишем теорему в виде:

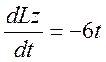
Разделяя переменные и интегрируя это уравнение, получим

              (*)

Для рассматриваемой механической системы

                (**)

где L_z^пл и L_z^D – кинетические моменты платформы и груза относительно оси z соответственно

Так как платформа вращается вокруг оси z, то . Значение  найдем по теореме Гюйгенса:

где - момент инерции относительно оси z:’, параллельной оси z и проходящей через центр С платформы.

Но, как известно, . Тогда  и, следовательно,

 .

Для определения  обратимся к рисунку и рассмотрим движение груза D как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси z переносным движением. Тогда абсолютна скорость груза . Так как груз D движется по закону s=CD=0.4t², то . Изображаем вектор  с учетом знака ds/dt (при ds/dt<0 направление этого вектора было бы противоположным). Затем, учитывая направление w, изображаем вектор , численно v_пер=w OD. Тогда, по теореме Вариньона

.

Но из рисунка видно, что OD²=R²+s²=R²+0.16t⁴. Подставляя эту величину в выражение для кинетического момента груза D, а затем значения кинетических моментов груза и платформы в равенство (**), получим с учетом данных задачи

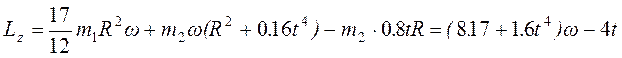
Тогда уравнение (*) примет вид

       (***)

Постоянную интегрирования С₁ определяем по начальным условиям: при t=0 w=w₀. Получим С₁=8.17w₀=16.34. При этом значении С₁ из уравнения (***) находим искомую зависимость w от t:

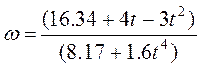, где t - в секундах, w - в с^-1.

Решение задачи  b

Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 2,3,5 и невесомых тел 1,4, соединенных нитями.

1. Изобразим действующие на систему силы: активные F, Fупр, Р3, Р2,  Р5, реакции N2, N3, натяжение нити S5, силу трения F2тр и момент М. Для определения угловой скорости вращения шкива 3  воспользуемся  теоремой об изменении кинетической энергии: 2. Определяем кинетическую энергию системы Т0 и Т. Так как в начальный момент система находилась в покое, то Т0=0.

Величина Т равна сумме энергий всех тел системы, имеющих массу:

Т=Т₃+ Т₂+ Т₅

Учитывая, что тело 3 вращается вокруг неподвижной оси, тело 2 движется поступательно, а подвижный блок 5 – плоскопараллельно, получим:

 (*)

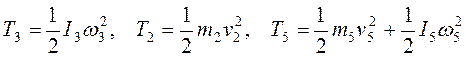Все входящие сюда скорости нужно выразить через искомую w₃. Для этого предварительно заметим, что v₅ (скорость центра подвижного блока 5) и w₅ (угловая скорость вращения блока 5) связаны соотношением w₅r₅=v₅, где r₅- радиус блока 5. Из кинематики также знаем, что v₅=v₂ / 2 и v₂=w₃r₃. Кроме того, входящие в (*) моменты инерции имеют значения

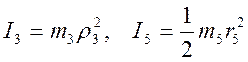
Подставляя все выражения для скоростей и моментов инерции в (*) получим окончательно выражение для кинетической энергии системы

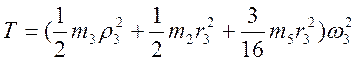
3. Теперь найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда точка приложения силы F пройдет путь s=0.2 м. Введя обозначения s₂ – перемещение груза 2, s₅ – перемещение центра подвижного блока 5, j₃ – угол поворота шкива 3, l₀ и l₁ – начальное и конечное удлинение пружины, получим

; ;  ;

 ; ;

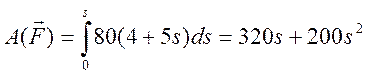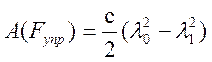
Работы остальных сил равны нулю, так как сила Р₃ и  реакция N₃ приложены к неподвижной оси шкива 3, реация N₂ перпендикулярна перемещению груза 2, а сила натяжения нити S₅ – приложена к мгновенному центру скоростей подвижного блока 5.

              По условию задачи l₀=0 (начальная деформация пружины равна нулю), тогда l₁=s₅ (удлинение пружины равно перемещению центра подвижного блока 5). Кроме того, перемещение s точки приложения силы F связано с углом поворота шкива 3 соотношением j₃R₃=s (то есть j₃=s/R₃). Величины s₂ и s₅ нужно также выразить через заданное перемещение s. При этом учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Так как, например, v₂=w₃r₃, то и s₂=j₃r₃; v₅=v₂ / 2, то и s₅=s₂ / 2. Тогда для перемещений s₂ и s₅ будем иметь: s₂=(r₃/R₃)s, s₅=(r₃/2R₃)s. При найденных значениях j₃, s₂ и s₅ для суммы вычисленных работ получим

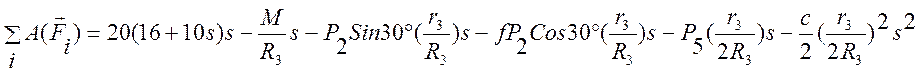
Подставляя полученные выражения для работы и кинетической энергии системы в теорему об изменении кинетической энергии будем иметь:

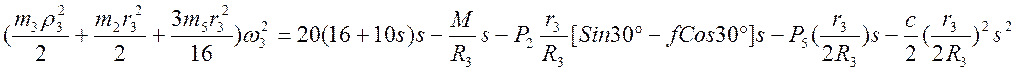
и, подставляя в это равенство численные значения заданных величин, найдем искомую угловую скорость: