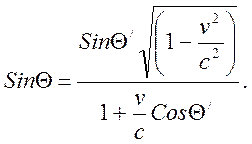 (7.10)
(7.10)
Ускорение в интервале углов Θ2~(1-v2/c2) имеет наибольшее значение из-за релятивистского сокращения времени и преобразований скорости. Подстановка ускорения (7.2) с учетом релятивистской массы в (7.9) и интегрирование по периоду обращения частицы дает следующее выражение:
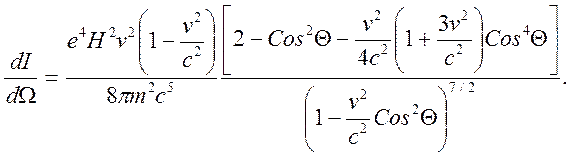
![]() (7.11)
(7.11)
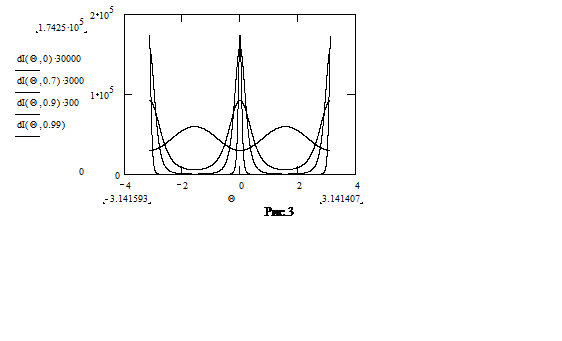
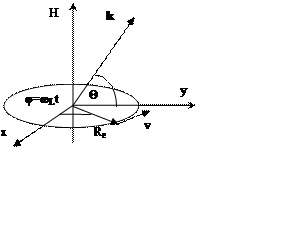
На рис. 3 приведены графики распределения (7.11) при отношениях v/c=0, 0.7, 0.9, 0.99. Видно, что угловое распределение сужается при увеличении скорости частицы. Отношение интенсивностей излучения под углом Θ=π/2 (перпендикулярно плоскости орбиты) и под углом Θ=0 в плоскости орбиты равно:
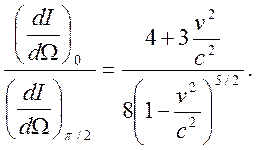 (7.12)
(7.12)
Для определения спектра синхротронного излучения нужно векторный потенциал (7.7) разложить в ряд Фурье, поскольку движение периодическое.
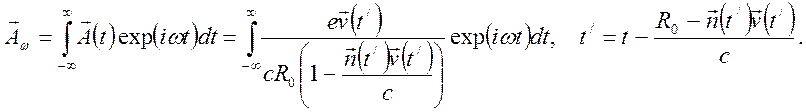 (7.13)
(7.13)
Переходя к интегрированию по времени t/ в движущейся системе координат можно в дальнейшем перейти к интегрированию по траектории частицы в силу периодичности движения:
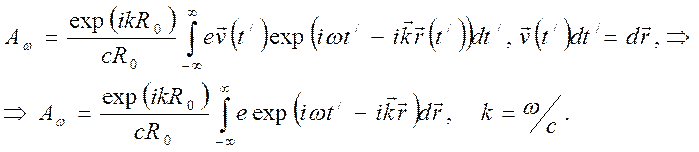 (7.14)
(7.14)
В (7.14) от интегрирования по бесконечности перейдем к интегрированию по периоду и к номеру гармоники n=ω/ωL.
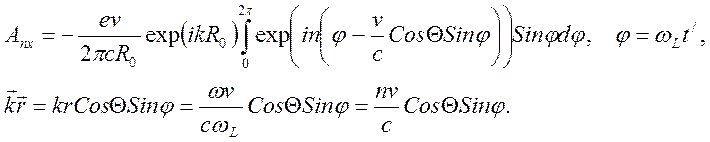 (7.15)
(7.15)
Y – компонента векторного потенциала вычисляется аналогично. Обе эти компоненты выражаются через функции Бесселя. Угловое распределение гармоник синхротронного излучения дается выражением:
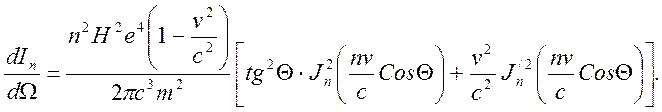 (7.16)
(7.16)
Полная интенсивность представляет собой набор гармоник, распределение интенсивностей в которых дается выражением:
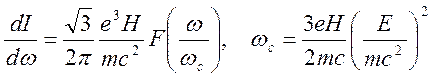 (7.17)
(7.17)
Функция F(x) имеет максимум при x=0.29 F(x=0.29)=0.92, F(0)=0, F(1)≈0.7, F(2) ≈0.35, F(3) ≈0.25, F(4) ≈0.1. Появление высших гармоник связано с импульсным характером излучения в течение времени, пока узкое угловое распределение попадает к наблюдателю:
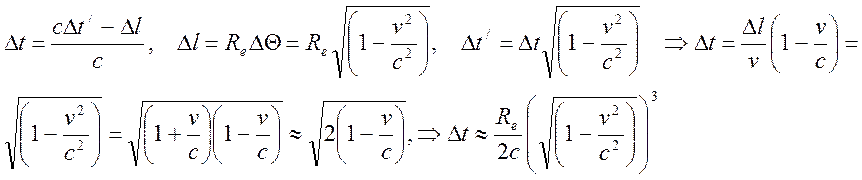 (7.18)
(7.18)
Для максимума излучения есть простая оценка:
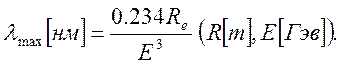 (7.20)
(7.20)
Например при Е=6 Гэв и Re=32 м λmax=0.035 нм. Энергия, теряемая электроном за один оборот, пропорциональна четвертой степени энергии:
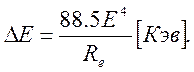 (7.22)
(7.22)
Экспериментально наблюдаемое излучение с хорошей точностью отвечает теоретическому и может служить эталоном.
Разновидностью синхротронного излучения служит магнитотормозное излучение, называемое ондуляторным. В синхротроне реально можно использовать лишь малую долю излучаемой энергии, пропорциональную ΔΘ/2π. Что составляет 10-4 – 10-5 всей энергии. В ондуляторе эффективность и монохроматичность существенно выше. В ондуляторе поток электронов проходит через систему знакопеременных магнитных полей, отклоняющих его в поперечном направлении. ондулятор обладает свойством пространственной дисперсии – излучение с большими длинами волн отклоняется на больший угол. Это позволяет выделять нужную область спектра простым диафрагмированием.
Рентгеновское излучение – тормозное излучение. Возникает при торможении пучка электронов в материале анода. Имеются характеристические линии - спонтанное излучение внутренних электронов.
Излучение из-за обратного эффекта Комптона. Отражение фотонов от релятивистского сгустка электронов. Эффективность преобразования повышается с ростом энергии пучка. Гэвный фотонный пучек наследует поляризацию исходного фотонного пучка. Действительно, законы сохранения энергии и импульса для релятивитких пучков частиц и отраженных фотонов запишутся в виде:
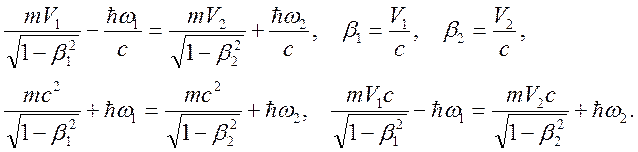
Складывая и вычитая уравнения для импульсов и энергий получим соотношения:
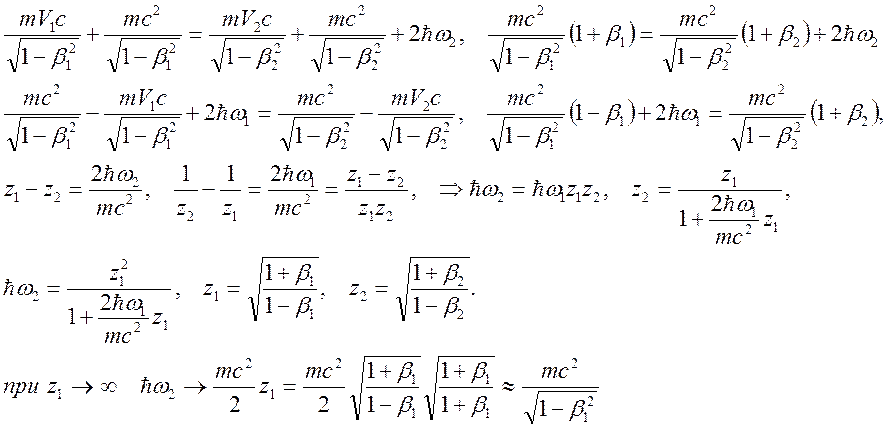
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.